 微分積分学
微分積分学 ガウス積分を極座標変換から求める|ヤコビアンが嬉しい計算
exp(-x²)の実数全体での広義積分は「ガウス積分」と呼ばれ,たとえば統計学では正規分布に関連してよく現れます.この記事では,極座標変換を用いてガウス積分を求めます.
 微分積分学
微分積分学 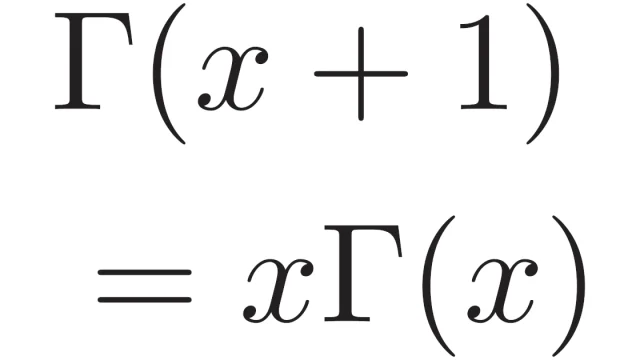 微分積分学
微分積分学 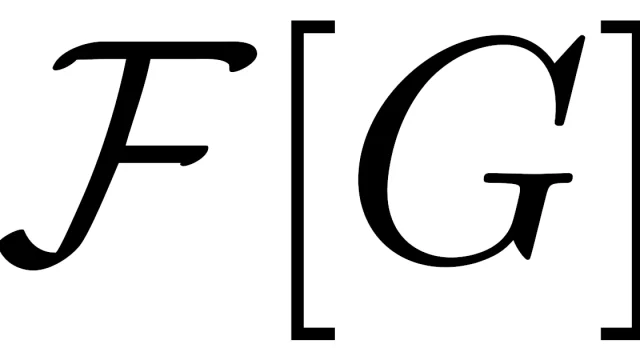 微分積分学
微分積分学  微分積分学
微分積分学  微分積分学
微分積分学