よく知られているように,実対称行列$A$に対して直交行列$P$をうまくとれば,$P^{-1}AP$が対角行列になります.
実行列$A$が正方行列でない場合にはこれに類似した特異値分解(SVD)があり,特異値分解は
- 画像圧縮:画像の質をそれほど落とさないようなデータ量(次元)の削減
- クラスタリングの効率化:対象を類似性で分類する際の効率化
などに応用されます.
この記事では
- 実対称行列の対角化と特異値分解$A=UBV^T$
- 行列の特異値分解を用いた低ランク近似
- 低ランク近似の具体例(画像圧縮)
- 特異値分解可能であることの証明
- 具体的な行列を手計算で特異値分解する
- 補足(非正方行列$\Sigma$への特異値分解$A=U\Sigma V^T$)
を順に解説します.
実対称行列の対角化と特異値分解$A=UBV^T$
まずは「実対称行列の直交行列による対角化」を復習し,これをもとに特異値分解がどのような分解であるかを解説します.
実対称行列は直交行列により対角化可能
次の定理は線形代数学の重要定理で,ご存知の方も多いでしょう.
$P^T P=I$を満たす実正方行列$P$を直交行列と定義するので,直交行列$P$は$P^{-1}=P^T$を満たすことに注意しましょう($P^T$は$P$の転置行列).
このことから対角化$P^{-1}AP=B$は
\begin{align*}A=PBP^{-1}=PBP^{T}\end{align*}
と変形することもできますね.
対角行列$B$への特異値分解$A=UBV^T$
実正方行列$A$が対称行列でなければ上の定理のようにひとつの直交行列$P$を用いて対角化(分解)することはできないのですが,2つの直交行列に対応する行列$U$, $V$を用いれば行列を分解することができます.
この分解を特異値分解と言います.
[特異値分解]ランクが$r$の実$m\times n$行列$A$に対して,等式
\begin{align*}A=UBV^T,\quad U^{T}U=V^{T}V=I_r\end{align*}
を満たす実$m\times r$行列$U$,実$n\times r$行列$U$,対角成分が正の$r$次対角行列$B$が存在する.
さらに,このとき$B$の$(k,k)$成分を$\sigma_k$とおくとき,$\sigma_1\ge\dots\ge\sigma_r>0$となるようにできる.
特異値分解は別の表し方をされることもよくあります.別の表し方の特異値分解については,この記事の最後で紹介しています.
行列$U$, $V$は正方行列ではないので直交行列とはいえませんが,直交行列の定義と(形式的に)同じ等式$U^{T}U=I_r$, $V^{T}V=I_r$を満たすことから,先ほどの「対称行列の直交行列による対角化」での直交行列$P$と対応していることが見て取れますね.
分解する行列$A$が対称行列でなくなった分,分解の形を対角化より広くしているわけですね.
上の[特異値分解]の定理において,対角行列$B$の対角成分を$A$の特異値という.
もし$A$が正方行列なら対角化$PAP^{-1}=B$の対角成分は固有値になるのでしたから,特異値は非対角成分の固有値に対応するものと捉えることができますね.
行列の特異値分解を用いた低ランク近似
ここで,行列の特異値分解を用いた低ランク近似を紹介します.
特異値分解のベクトルを用いた書き換え
$m\times n$行列$A$の対角行列$B$を用いた特異値分解$A=UBV^T$について,$U$, $V$, $B$をそれぞれ
\begin{align*}&\begin{aligned}&U=[\m{u}_1,\m{u}_2,\dots,\m{u}_r],
\\&V=[\m{v}_1,\m{v}_2,\dots,\m{v}_r],\end{aligned}
&B=\bmat{\sigma_1&0&\dots&0\\0&\sigma_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\sigma_r}
\end{align*}
とすると,
\begin{align*}A&=[\m{u}_1,\m{u}_2,\dots,\m{u}_r]
\bmat{\sigma_1&0&\dots&0\\0&\sigma_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\sigma_r}
\bmat{{\m{v}_1}^T\\{\m{v}_2}^T\\\vdots\\{\m{v}_r}^T}
\\&=[\sigma_1\m{u}_1,\sigma_2\m{u}_2,\dots,\sigma_r\m{u}_r]
\bmat{{\m{v}_1}^T\\{\m{v}_2}^T\\\vdots\\{\m{v}_r}^T}
\\&=\sigma_1\m{u}_1{\m{v}_1}^T+\dots+\sigma_r\m{u}_r{\m{v}_r}^T\bra{=\sum_{i=1}^{r}\sigma_i\m{u}_i{\m{v}_i}^T}\end{align*}
となりますね.ただし,列ベクトル$\m{x}$に対して,$\m{x}$の転置行列を$\m{x}^T$で表します.
最後の和では各項の$\m{u}_{k}{\m{v}_{k}}^T$($k=1,2,\dots,r$)が$m\times n$行列になっています.つまり,最後の和は$r$個の$m\times n$行列の和になっています.
特異値分解を用いた行列の低ランク近似
行列の特異値は全て正なので$\sigma_1,\dots,\sigma_r>0$で,特異値分解
\begin{align*}A=\sigma_1\m{u}_1{\m{v}_1}^T+\dots+\sigma_r\m{u}_r{\m{v}_r}^T\end{align*}
の右辺で小さい$\sigma_k$をいくつか0にしてもそれほど大きな影響はないと考えられます.
そこで行列$A$の特異値を小さい方からいくつか0にしてできる行列を$A$の低ランク近似といいます.
特異値が$\sigma_1,\sigma_2,\dots,\sigma_r$($\sigma_1\ge\sigma_2\ge\dots\ge\sigma_r>0$)の行列$A$の特異値分解
\begin{align*}A&=\sigma_1\m{u}_1{\m{v}_1}^T+\dots+\sigma_r\m{u}_r{\m{v}_r}^T
\\&\bra{=[\m{u}_1,\dots,\m{u}_r]\bmat{\sigma_1&&O\\&\ddots&\\O&&\sigma_r}\bmat{{\m{v}_1}^T\\\vdots\\{\m{v}_r}^T}}\end{align*}
を考える.$s<r$なる正の整数$s$に対して,行列
\begin{align*}A_s&=\sigma_1\m{u}_1{\m{v}_1}^T+\dots+\sigma_s\m{u}_s{\m{v}_s}^T
\\&\bra{=[\m{u}_1,\dots,\m{u}_s]\bmat{\sigma_1&&O\\&\ddots&\\O&&\sigma_s}\bmat{{\m{v}_1}^T\\\vdots\\{\m{v}_s}^T}}\end{align*}
を$A$のランク$s$の低ランク近似という.
このときの$A_s$は$\rank{A_s}=s$を満たしており,ランクが$s$の$m\times n$行列の中でも$A$の「良い近似」になっていることが証明できますが,この記事では割愛します.
たとえば,ランクが100の行列$A$は
\begin{align*}A=\sigma_1\m{u}_1{\m{v}_1}^T+\dots+\sigma_{100}\m{u}_{100}{\m{v}_{100}}^T&
\\(\sigma_1\ge\dots\ge\sigma_{100}>0)&\end{align*}
と特異値分解でき,$A$ののランク80の低ランク近似は
\begin{align*}A_{80}=\sigma_1\m{u}_1{\m{v}_1}^T+\dots+\sigma_{80}\m{u}_{80}{\m{v}_{80}}^T\end{align*}
となります.
低ランク近似の累積寄与率
行列$A$の低ランク近似において,どれだけの特異値$\sigma_k$を残しているかは,$A$の情報をどれだけ残しているかということでもあります.
そこで,低ランク近似でどれくらい情報が残っているかを示す指標として累積寄与率を次で定めます.
特異値$\sigma_1,\sigma_2,\dots,\sigma_r$($\sigma_1\ge\dots\ge\sigma_r>0$)をもつ行列$A$に対して,
\begin{align*}\frac{\sigma_1+\sigma_2+\dots+\sigma_s}{\sigma_1+\sigma_2+\dots+\sigma_r}\end{align*}
をランク$s$の低ランク近似の累積寄与率という.
累積寄与率は(分子)≦(分母)なので$\rho\le1$となっており,分子の項が少ないほど0に近付いていくことから,累積寄与率が大きいほど情報が失われていないといえますね.
たとえば,特異値$\sigma_1,\sigma_2,\dots,\sigma_{100}$($\sigma_1\ge\dots\ge\sigma_{100}>0$)の行列$A$の,ランク80の低ランク近似の累積寄与率は
\begin{align*}\frac{\sigma_1+\sigma_2+\dots+\sigma_{80}}{\sigma_1+\sigma_2+\dots+\sigma_{100}}\end{align*}
となります.
低ランク近似の具体例(画像圧縮)
具体例として,次の4×5サイズの顔のモノクロ画像の圧縮を考えましょう.
目の部分は白50%,黒50%のグレーで,口の部分は黒100%となっています.
この程度の画像ならデータ量が小さいので画像圧縮する必要は特にありませんが,より巨大な画像を圧縮したい場合も同じように圧縮できます.
ステップ1:モノクロ画像を行列$A$にする
最初にこのモノクロ画像を4×5行列$A$にします.
「黒100%」を1,「白100%」を0として表すと,上の顔の画像は
\begin{align*}A=\bmat{0&1/2&0&1/2&0\\0&0&0&0&0\\1&0&0&0&1\\0&1&1&1&0}\end{align*}
と表すことができますね.
なお,行列$A$のランクは$\rank{A}=3$なので,この時点で特異値分解$A=UBV^T$の対角行列$B$は3次正方行列になることが分かります.
「黒100%」を0,「白100%」を255とするグレースケールでの表し方をすることも多いです.
ステップ2:モノクロ画像の行列$A$を特異値分解する
行列$A$を実際に特異値分解すると,
\begin{align*}A=\frac{\sqrt{7+\sqrt{41}}}{2}\m{u}_1{\m{v}_1}^T+\sqrt{2}\m{u}_2{\m{v}_2}^T+\frac{\sqrt{7-\sqrt{41}}}{2}\m{u}_3{\m{v}_3}^T\end{align*}
となります($\frac{\sqrt{7+\sqrt{41}}}{2}>\sqrt{2}>\frac{\sqrt{7-\sqrt{41}}}{2}$).ただし,
\begin{align*}&\m{v}_1\approx\sbmat{0\\0.6059\\0.5155\\0.6059\\0},\quad
\m{v}_2\approx\sbmat{0.7071\\0\\0\\0\\0.7071},\quad
\m{v}_3\approx\sbmat{0\\0.3645\\0.8569\\-0.3645\\0},
\\&\m{u}_1\approx\sbmat{0.3310\\0\\0\\0.9436},\quad
\m{u}_2=\sbmat{0\\0\\1\\0},\quad
\m{u}_3\approx\sbmat{-0.9436\\0\\0\\0.3310}\end{align*}
となっています.この記事の後半の具体例で,手計算によりこの特異値分解を厳密に求めています.
これくらいなら手計算でも頑張れますが,大きなサイズの行列を手計算により特異値分解するのは現実的ではありません.大きなサイズの行列を特異値分解するにはプログラミングを使うのが普通です.
ステップ3:モノクロ画像の行列$A$を低ランク近似する
いまは$\rank{A}=3$なので,行列$A$の
- ランク2の低ランク近似$A_2$
- ランク1の低ランク近似$A_1$
が考えられ,それぞれ
\begin{align*}A_2&=\frac{\sqrt{7+\sqrt{41}}}{2}\m{u}_1{\m{v}_1}^T+\sqrt{2}\m{u}_2{\m{v}_2}^T
\approx\bmat{0&0.3671&0.3123&0.3671&0\\0&0&0&0&0\\1&0&0&0&1\\0&1.0466&0.8904&1.0466&0}
\\A_1&=\frac{\sqrt{7+\sqrt{41}}}{2}\m{u}_1{\m{v}_1}^T
\approx\bmat{0&0.3671&0.3123&0.3671&0\\0&0&0&0&0\\0&0&0&0&0\\0&1.0466&0.8904&1.0466&0}\end{align*}
となります.また,累積寄与率はそれぞれ
\begin{align*}\\&\frac{\frac{\sqrt{7+\sqrt{41}}}{2}+\sqrt{2}}{\frac{\sqrt{7+\sqrt{41}}}{2}+\sqrt{2}+\frac{\sqrt{7-\sqrt{41}}}{2}}\approx0.8936,
\\&\frac{\frac{\sqrt{7+\sqrt{41}}}{2}}{\frac{\sqrt{7+\sqrt{41}}}{2}+\sqrt{2}+\frac{\sqrt{7-\sqrt{41}}}{2}}\approx0.5041\end{align*}
なので,$A_2$は$A$の約90%の情報を残しており,$A_1$は$A$の約50%の情報を残していると捉えることができますね.
ステップ4:(必要なら処理をして)画像に戻す
低ランク近似$A_s$の全ての成分が0以上1以下の範囲にあれば,そのまま画像に戻すことで画像圧縮が完成します.
しかし,今回の$A_2$, $A_1$はいずれも1を超える成分をもっています.この場合は低ランク近似$A_2$, $A_1$に処理を施し,全ての成分を0以上1以下にした行列を作り,それを画像に戻します.
今回はクリッピングという簡単な処理を施します.クリッピングとは0未満の成分を0にし,1を超える成分を1にするという処理です.
行列を実数倍して成分を0以上1以下に収める方法など,クリッピングの他にも様々な処理が考えられます.
クリッピングにより,ステップ3で得られた低ランク近似$A_2$, $A_1$は
\begin{align*}A_2’&\approx\bmat{0&0.3671&0.3123&0.3671&0\\0&0&0&0&0\\1&0&0&0&1\\0&1&0.8904&1&0}
\\A_1’&\approx\bmat{0&0.3671&0.3123&0.3671&0\\0&0&0&0&0\\0&0&0&0&0\\0&1&0.8904&1&0}\end{align*}
となり,これらを画像に直すと次のようになります.
$A_2$は目が繋がってしまっているものの笑っているようには見えますが,$A_1$は3行目の成分が全て0になり表情が分からなくなりました.このように,ランクを下げるほど情報が失われていることが見てとれますね.
特異値分解可能であることの証明
[特異値分解(再掲)]ランクが$r$の実$m\times n$行列$A$に対して,等式
\begin{align*}A=UBV^T,\quad U^{T}U=V^{T}V=I_r\end{align*}
を満たす実$m\times r$行列$U$,実$n\times r$行列$V$,対角成分が正の$r$次対角行列$B$が存在する.
さらに,このとき$B$の$(k,k)$成分を$\sigma_k$とおくとき,$\sigma_1\ge\dots\ge\sigma_r>0$となるようにできる.
行列$U$, $V$の構成
$\rank{A}=r$より$\rank{A^TA}=r$なので,行列$A^TA$の0でない固有値は重複を許して$r$個存在する.行列$A^TA$の0でない固有値を$\lambda_1,\lambda_2,\dots,\lambda_r$とし,$\lambda_1\ge\dots\ge\lambda_r$を満たすとする.
また,行列$A^TA$は実対称行列だから$\lambda_1,\lambda_2,\dots,\lambda_r$に属する固有ベクトル$\m{v}_1,\m{v}_2,\dots,\m{v}_r$が正規直交系であるようにとれる.さらに,任意の$i\in\{1,2,\dots,r\}$に対して
\begin{align*}\lambda_i&=\lambda_i\|\m{v}_i\|^2={\m{v}_i}^T\m{v}_i={\m{v}_i}^T(\lambda_i\m{v}_i)={\m{v}_i}^T(A^TA\m{v}_i)
\\&=({\m{v}_i}^TA^T)(A\m{v}_i)=(A{\m{v}_i})^T(A\m{v}_i)=\|A\m{v}_i\|^2\ge0\end{align*}
なので,$\lambda_i\neq0$と併せて$\lambda_i>0$である.ここで,実$m\times r$行列$U$,実$n\times r$行列$V$を
\begin{align*}&V=[\m{v}_1,\m{v}_2,\dots,\m{v}_r],
\\&U=A\brc{\frac{\m{v}_1}{\sqrt{\lambda_1}},\frac{\m{v}_2}{\sqrt{\lambda_2}},\dots,\frac{\m{v}_r}{\sqrt{\lambda_r}}}
\bra{=\brc{\frac{A\m{v}_1}{\sqrt{\lambda_1}},\frac{A\m{v}_2}{\sqrt{\lambda_2}},\dots,\frac{A\m{v}_r}{\sqrt{\lambda_r}}}}\end{align*}
とおく.
$V^{T}V=I_r$となることの証明
$\m{v}_1,\m{v}_2,\dots,\m{v}_r$は正規直交系なので
\begin{align*}{\m{v}_i}^T\m{v}_j=\begin{cases}1&(i=j)\\0&(i\neq j)\end{cases}\quad\dots(*)\end{align*}
だから,$V$の定義より
\begin{align*}V^TV&=\bmat{{\m{v}_1}^T\\{\m{v}_2}^T\\\vdots\\{\m{v}_r}^T}[\m{v}_1,\m{v}_2,\dots,\m{v}_r]
=\bmat{{\m{v}_1}^T\m{v}_1&{\m{v}_1}^T\m{v}_2&\dots&{\m{v}_1}^T\m{v}_r\\
{\m{v}_2}^T\m{v}_1&{\m{v}_2}^T\m{v}_2&\ddots&{\m{v}_2}^T\m{v}_r\\
\vdots&\ddots&\ddots&\vdots\\
{\m{v}_1}^T\m{v}_1&{\m{v}_r}^T\m{v}_2&\dots&{\m{v}_r}^T\m{v}_r}
=I_r\end{align*}
が成り立つ.
$U^{T}U=I_r$となることの証明
$U$の定義より
\begin{align*}U^T&=\bra{A\brc{\frac{\m{v}_1}{\sqrt{\lambda_1}},\frac{\m{v}_2}{\sqrt{\lambda_2}},\dots,\frac{\m{v}_r}{\sqrt{\lambda_r}}}}^T
=\bmat{\frac{1}{\sqrt{\lambda_1}}{\m{v}_1}^T\\\frac{1}{\sqrt{\lambda_2}}{\m{v}_2}^T\\\vdots\\\frac{1}{\sqrt{\lambda_r}}{\m{v}_r}^T}A^T,
\\A^TU&=\brc{\frac{A^TA\m{v}_1}{\sqrt{\lambda_1}},\frac{A^TA\m{v}_2}{\sqrt{\lambda_2}},\dots,\frac{A^TA\m{v}_r}{\sqrt{\lambda_r}}}
\\&=\brc{\frac{\lambda_1\m{v}_1}{\sqrt{\lambda_1}},\frac{\lambda_2\m{v}_2}{\sqrt{\lambda_2}},\dots,\frac{\lambda_r\m{v}_r}{\sqrt{\lambda_r}}}
=\brc{\sqrt{\lambda_1}\m{v}_1,\sqrt{\lambda_2}\m{v}_2,\dots,\sqrt{\lambda_r}\m{v}_r}\end{align*}
なので,$(*)$と併せて
\begin{align*}U^TU&=\bmat{\frac{1}{\sqrt{\lambda_1}}{\m{v}_1}^T\\\frac{1}{\sqrt{\lambda_2}}{\m{v}_2}^T\\\vdots\\\frac{1}{\sqrt{\lambda_r}}{\m{v}_r}^T}A^TU
=\bmat{\frac{1}{\sqrt{\lambda_1}}{\m{v}_1}^T\\\frac{1}{\sqrt{\lambda_2}}{\m{v}_2}^T\\\vdots\\\frac{1}{\sqrt{\lambda_r}}{\m{v}_r}^T}
\brc{\sqrt{\lambda_1}\m{v}_1,\sqrt{\lambda_2}\m{v}_2,\dots,\sqrt{\lambda_r}\m{v}_r}
\\&=\bmat{{\m{v}_1}^T\m{v}_1&\sqrt{\frac{\lambda_2}{\lambda_1}}{\m{v}_1}^T\m{v}_2&\dots&\sqrt{\frac{\lambda_r}{\lambda_1}}{\m{v}_1}^T\m{v}_r\\
\sqrt{\frac{\lambda_1}{\lambda_2}}{\m{v}_2}^T\m{v}_1&{\m{v}_2}^T\m{v}_2&\dots&\sqrt{\frac{\lambda_r}{\lambda_2}}{\m{v}_2}^T\m{v}_r\\
\vdots&\ddots&\ddots&\vdots\\
\sqrt{\frac{\lambda_1}{\lambda_r}}{\m{v}_r}^T\m{v}_1&\sqrt{\frac{\lambda_2}{\lambda_r}}{\m{v}_r}^T\m{v}_2&\dots&{\m{v}_r}^T\m{v}_r}
=I_r\end{align*}
が成り立つ.
$A=UBV^T$となることの証明
$V$の定義より
\begin{align*}A^TAV&=A^TA[\m{v}_1,\m{v}_2,\dots,\m{v}_r]
\\&=[A^TA\m{v}_1,A^TA\m{v}_2,\dots,A^TA\m{v}_r]
\\&=[\lambda_1\m{v}_1,\lambda_2\m{v}_2,\dots,\lambda_r\m{v}_r]\end{align*}
なので,$V^TV=U^TU=I_r$を示す際の計算と同様に
\begin{align*}U^TAV&=\bmat{\frac{1}{\sqrt{\lambda_1}}{\m{v}_1}^T\\\frac{1}{\sqrt{\lambda_2}}{\m{v}_2}^T\\\vdots\\\frac{1}{\sqrt{\lambda_r}}{\m{v}_r}^T}
[\lambda_1\m{v}_1,\lambda_2\m{v}_2,\dots,\lambda_r\m{v}_r]
\\&=\bmat{\sqrt{\lambda_1}{\m{v}_1}^T\m{v}_1&\frac{\lambda_2}{\sqrt{\lambda_1}}{\m{v}_1}^T\m{v}_2&\dots&\frac{\lambda_r}{\sqrt{\lambda_1}}{\m{v}_1}^T\m{v}_r\\
\frac{\lambda_1}{\sqrt{\lambda_2}}{\m{v}_2}^T\m{v}_1&\sqrt{\lambda_2}{\m{v}_2}^T\m{v}_2&\ddots&\frac{\lambda_r}{\sqrt{\lambda_2}}{\m{v}_2}^T\m{v}_r\\
\vdots&\ddots&\ddots&\vdots\\
\frac{\lambda_1}{\sqrt{\lambda_r}}{\m{v}_1}^T\m{v}_1&\frac{\lambda_2}{\sqrt{\lambda_r}}{\m{v}_r}^T\m{v}_2&\dots&\sqrt{\lambda_r}{\m{v}_r}^T\m{v}_r}
\\&=\bmat{\sqrt{\lambda_1}&0&\dots&0\\0&\sqrt{\lambda_2}&\ddots&0\\\vdots&\ddots&\ddots&\vdots\\0&0&\dots&\sqrt{\lambda_r}}\end{align*}
が成り立つ.よって,両辺に左から$U$をかけ,右から$V^T$をかければ,$V^TV=U^TU=I_r$と併せて
\begin{align*}A=U\bmat{\sqrt{\lambda_1}&0&\dots&0\\0&\sqrt{\lambda_2}&\ddots&0\\\vdots&\ddots&\ddots&\vdots\\0&0&\dots&\sqrt{\lambda_r}}V^T\end{align*}
が従う.
具体的な行列を手計算で特異値分解する
上でみた特異値分解可能性の証明から,特異値分解$A=UBV^T$について,
- 行列$A$の特異値$\sigma_i$は,行列$A^TA$の正の(0でない)固有値$\lambda_i$の正の平方根$\sqrt{\lambda_i}$に一致する($i=1,2,\dots,r$)
- $\m{v}_i$を行列$A^TA$の正の固有値$\lambda_i$の長さ1の固有ベクトルとする($i=1,2,\dots,r$)と,
- $V$は$\m{v}_1,\dots,\m{v}_r$を並べてできる行列
- $U$は$\frac{1}{\sqrt{\lambda_1}}A\m{v}_1,\dots,\frac{1}{\sqrt{\lambda_r}}A\m{v}_r$を並べてできる行列
ととれる
ということが分かりますね.
このことを用いて,画像圧縮のところで考えた4×5行列
\begin{align*}A=\bmat{0&1/2&0&1/2&0\\0&0&0&0&0\\1&0&0&0&1\\0&1&1&1&0}\end{align*}
を実際に手計算で特異値分解しておきましょう.
ステップ1:行列$A^TA$の固有値を求める
計算により行列$A^TA$は
\begin{align*}A^TA=\bmat{0&0&1&0\\1/2&0&0&1\\0&0&0&1\\1/2&0&0&1\\0&0&1&0}\bmat{0&1/2&0&1/2&0\\0&0&0&0&0\\1&0&0&0&1\\0&1&1&1&0}
=\bmat{1&0&0&0&1\\0&5/4&1&5/4&0\\0&1&1&1&0\\0&5/4&1&5/4&0\\1&0&0&0&1}\end{align*}
なので,行列$A^TA$の固有多項式は
\begin{align*}&|xI-A^TA|=\vmat{x-1&0&0&0&-1\\0&x-5/4&-1&-5/4&0\\0&-1&x-1&-1&0\\0&-5/4&-1&x-5/4&0\\-1&0&0&0&x-1}
\\&=(x-1)\vmat{x-5/4&-1&-5/4&0\\-1&x-1&-1&0\\-5/4&-1&x-5/4&0\\0&0&0&x-1}
+(-1)\vmat{0&x-5/4&-1&-5/4\\0&-1&x-1&-1\\0&-5/4&-1&x-5/4\\-1&0&0&0}
\\&=(x-1)^2\vmat{x-5/4&-1&-5/4\\-1&x-1&-1\\-5/4&-1&x-5/4}
-(-1)^2\vmat{x-5/4&-1&-5/4\\-1&x-1&-1\\-5/4&-1&x-5/4}
\\&=x(x-2)\vmat{x-5/4&-1&-5/4\\-1&x-1&-1\\-5/4&-1&x-5/4}\end{align*}
となります.
2つ目の等号,3つ目の等号で余因子展開を使っています.
最後の行列式の部分は
\begin{align*}&\vmat{x-5/4&-1&-5/4\\-1&x-1&-1\\-5/4&-1&x-5/4}
=\vmat{x&0&-x\\-1&x-1&-1\\-5/4&-1&x-5/4}
\\&=x\vmat{1&0&-1\\-1&x-1&-1\\-5/4&-1&x-5/4}
=x\vmat{1&0&-1\\0&x-1&-2\\0&-1&x-5/2}
\\&=x\brb{(x-1)\bra{x-\frac{5}{2}}-2}
=\frac{1}{2}x(2x^2-7x+1)\end{align*}
となるので,
\begin{align*}|xI-A^TA|=\frac{1}{2}x^2(x-2)(2x^2-7x+1)\end{align*}
です.よって,固有方程式$|xI-A^TA|=0$を解いて,$A^TA$の固有値は
\begin{align*}0,0,2,\frac{7+\sqrt{41}}{4},\frac{7-\sqrt{41}}{4}\end{align*}
と分かります.
ステップ2:特異値分解$A=UBV^T$の$B$を求める
ここで行列$A^TA$の正の固有値を
\begin{align*}\lambda_1=\frac{7+\sqrt{41}}{4},\quad
\lambda_2=2,\quad
\lambda_3=\frac{7-\sqrt{41}}{4}\end{align*}
とおきましょう.特異値分解行列$A$の特異値は行列$A^TA$の正の固有値の正の平方根に一致するのでしたから,行列$A$の特異値は
\begin{align*}\sqrt{\lambda_1}=\frac{\sqrt{7+\sqrt{41}}}{2},\quad
\sqrt{\lambda_2}=\sqrt{2},\quad
\sqrt{\lambda_3}=\frac{\sqrt{7-\sqrt{41}}}{2}\end{align*}
ですから,$\sqrt{\lambda_1}>\sqrt{\lambda_2}>\sqrt{\lambda_3}$で,$A$の特異値分解は
\begin{align*}A=UBV^T,\quad B=\bmat{\sqrt{\lambda_1}&0&0\\0&\sqrt{\lambda_2}&0\\0&0&\sqrt{\lambda_3}}\end{align*}
となります.
ステップ3:行列$A^TA$の正の固有値に属する固有ベクトルを求める
$A^TA$の正の固有値に属する固有ベクトルを求めます.一般に行列$X$の固有値$\lambda$に属する固有ベクトル$\m{p}$は
\begin{align*}X\m{p}=\lambda\m{p}\iff(X-\lambda I)\m{p}=\m{0}\end{align*}
を満たす$\m{0}$でないベクトルなので,掃き出し法により$X-\lambda I$の行基本変形から固有ベクトルが得られることを思い出しておきましょう.
固有値2に属する固有ベクトル
$A^TA-2I=\sbmat{-1&0&0&0&1\\0&-3/4&1&5/4&0\\0&1&-1&1&0\\0&5/4&1&-3/4&0\\1&0&0&0&-1}$です.成分の0の位置に注意すると,$A^TA$は本質的に
\begin{align*}\bmat{-1&1\\1&-1},\quad\bmat{-3/4&1&5/4\\1&-1&1\\5/4&1&-3/4}\end{align*}
の2つの行列からなっています.これらの行列は,行基本変形により
\begin{align*}&\bmat{-1&1\\1&-1}\to\bmat{-1&1\\0&0},
\\&\bmat{-3/4&1&5/4\\1&-1&1\\5/4&1&-3/4}\to\bmat{-3&4&5\\1&-1&1\\5&4&-3}\to\bmat{1&0&9\\1&-1&1\\9&0&1}
\\&\to\bmat{1&0&9\\0&-1&-8\\0&0&-80}\to\bmat{1&0&9\\0&-1&-8\\0&0&-80}\to\bmat{1&0&0\\0&1&0\\0&0&1}
\end{align*}
となるので,$A^TA-2I\to\sbmat{-1&0&0&0&1\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&0}$と行基本変形でき,行列$A^TA$の固有値2に属する固有ベクトルは
\begin{align*}k\bmat{1\\0\\0\\0\\1}\quad(k\in\R\setminus\{0\})\end{align*}
と分かります(掃き出し法).
固有値$\frac{7\pm\sqrt{41}}{4}$に属する固有ベクトル
$\lambda=\frac{7\pm\sqrt{41}}{4}$とおくと,$A^TA-\lambda I=\sbmat{1-\lambda&0&0&0&1\\0&5/4-\lambda&1&5/4&0\\0&1&1-\lambda&1&0\\0&5/4&1&5/4-\lambda&0\\1&0&0&0&1-\lambda}$です.成分の0の位置に注意すると,$A^TA$は本質的に
\begin{align*}\bmat{1-\lambda&1\\1&1-\lambda},\quad\bmat{5/4-\lambda&1&5/4\\1&1-\lambda&1\\5/4&1&5/4-\lambda}\end{align*}
の2つの行列からなっています.これらの行列は,行基本変形により
\begin{align*}&\bmat{1-\lambda&1\\1&1-\lambda}
\to\bmat{0&1-(1-\lambda)^2\\1&1-\lambda}
\to\bmat{0&2\lambda-\lambda^2\\1&1-\lambda}
\to\bmat{1&0\\0&1},
\\&\bmat{5/4-\lambda&1&5/4\\1&1-\lambda&1\\5/4&1&5/4-\lambda}
\to\bmat{5-4\lambda&4&5\\1&1-\lambda&1\\5&4&5-4\lambda}
\\&\to\bmat{-4\lambda&0&4\lambda\\1&1-\lambda&1\\5&4&5-4\lambda}
\to\bmat{-1&0&1\\1&1-\lambda&1\\5&4&5-4\lambda}
\\&\to\bmat{-1&0&1\\0&1-\lambda&2\\0&4&10-4\lambda}
\to\bmat{-1&0&1\\0&1-\lambda&2\\0&0&0}\end{align*}
となります.
よって,$A^TA-\lambda I\to\sbmat{1&0&0&0&0\\0&-1&0&1&0\\0&0&1-\lambda&2&0\\0&0&0&0&0\\0&0&0&0&1}$と行基本変形でき,行列$A^TA$の固有値$\lambda$に属する固有ベクトルは
\begin{align*}k\bmat{0\\\lambda-1\\2\\\lambda-1\\0}\quad(k\in\R\setminus\{0\})\end{align*}
と分かります(掃き出し法).
ステップ4:特異値分解$A=UBV^T$の$U$, $V$を求める
ステップ3より
\begin{align*}\m{v}_1=\frac{1}{\sqrt{3\lambda_1+5}}\bmat{0\\\lambda_1-1\\2\\\lambda_1-1\\0},\quad
\m{v}_2=\frac{1}{\sqrt{2}}\bmat{1\\0\\0\\0\\1},\quad
\m{v}_3=\frac{1}{\sqrt{3\lambda_3+5}}\bmat{0\\\lambda_3-1\\2\\\lambda_3-1\\0}\end{align*}
はそれぞれ$A^TA$の固有値$\lambda_1,\lambda_2,\lambda_3$に属する固有ベクトルで長さは正規直交系をなします.
$\lambda_i$は$2x^2-7x+1=0$の解なので,固有ベクトル$\sbmat{0\\\lambda_i-1\\2\\\lambda_i-1\\0}$の長さは
\begin{align*}\sqrt{(\lambda_i-1)^2+2^2+(\lambda_i-1)^2}=\sqrt{3\lambda_i+5}\end{align*}
と計算できます($i=1,3$).
さらに$\m{u}_i=\frac{A\m{v}_i}{\sqrt{\lambda_i}}$($i=1,2,3$)とおいて,特異値分解$A=UBV^T$の$U$, $V$は
\begin{align*}V=[\m{v}_1,\m{v}_2,\m{v}_3],\quad
U=[\m{u}_1,\m{u}_2,\m{u}_3]\end{align*}
ととることができるのでした.実際に$\lambda_i$, $\m{v}_1$を代入すると,
\begin{align*}&\m{v}_1=\frac{2}{\sqrt{41+3\sqrt{41}}}\sbmat{0\\\frac{3+\sqrt{41}}{4}\\2\\\frac{3+\sqrt{41}}{4}\\0},\quad
\m{v}_2=\frac{1}{\sqrt{2}}\bmat{1\\0\\0\\0\\1},\quad
\m{v}_3=\frac{2}{\sqrt{41-3\sqrt{41}}}\sbmat{0\\\frac{3-\sqrt{41}}{4}\\2\\\frac{3-\sqrt{41}}{4}\\0},
\\&\m{u}_1=\frac{4}{410+62\sqrt{41}}\sbmat{\frac{3+\sqrt{41}}{4}\\0\\0\\\frac{7+\sqrt{41}}{2}},\quad
\m{u}_2=\sbmat{0\\0\\1\\0},\quad
\m{u}_3=\frac{4}{410-62\sqrt{41}}\sbmat{\frac{3-\sqrt{41}}{4}\\0\\0\\\frac{7-\sqrt{41}}{2}}\end{align*}
となります.これで特異値分解$A=UBV^T$が得られました.
補足(非正方行列$\Sigma$への特異値分解$A=U\Sigma V^T$)
ここまで考えてきた特異値分解と本質的には全く同じですが,次の形で書かれることもよくあります.
[特異値分解2]ランクが$r$の実$m\times n$行列$A$に対して,等式
\begin{align*}A=U\Sigma V^T,\quad
\Sigma=\bmat{B&O\\O&O}\end{align*}
を満たす$m$次直交行列$U$,$n$次直交行列$V$,対角成分が0以上の$r$次対角行列$B$が存在する.
さらに,このとき$B$の$(k,k)$成分を$\sigma_k$とおくとき,$\sigma_1\ge\dots\ge\sigma_r\ge0$となるようにできる.
先ほどの[特異値分解]の0も含めた固有値の固有ベクトルも考えると,大体[特異値分解2]の証明になります.そのため,こちらは略証に留めます.
$n$次正方行列$A^TA$の固有値を,重複を許して$\lambda_1,\dots,\lambda_n$($\lambda_1\ge\dots\ge\lambda_n\ge0$)とおく.$A^TA$の固有値は全て0以上で,$\rank{A}=r$だから$\lambda_1,\dots,\lambda_r>0$(かつ$\lambda_{r+1}=\dots=\lambda_n=0$)である,
また,$A^TA$は実対称だから,$\lambda_1,\dots,\lambda_n$それぞれに属する固有ベクトル$\m{v}_1,\dots,\m{v}_n\in\R^n$が存在して,$V:=[\m{v}_1,\dots,\m{v}_n]$は$n$次直交行列となる.また,
\begin{align*}\m{u}_i:=\frac{A\m{v}_i}{\sqrt{\lambda_i}}\quad(i=1,2,\dots,r)\end{align*}
とおくと,$\m{u}_i\in\R^m$($i=1,2,\dots,r$)で$\m{u}_1,\dots,\m{u}_r$は正規直交系なので,適当な正規ベクトル$\m{u}_{r+1},\dots,\m{u}_{m}\in\R^m$をとれば$U:=[\m{u}_1,\m{u}_2,\dots,\m{u}_m]$は$m$次直交行列である.このとき,
\begin{align*}U^TAV=\bmat{B&O_{r,n-r}\\O_{m-r,r}&O_{m-r,n-r}},\quad
B=\bmat{\sqrt{\lambda_1}&0&\dots&0\\0&\sqrt{\lambda_2}&\ddots&0\\\vdots&\ddots&\ddots&\vdots\\0&0&\dots&\sqrt{\lambda_r}}\end{align*}
が成り立ち,両辺に左から$U$をかけ,右から$V^T$をかければ,$U$, $V$が直交行列であることと併せて従う.

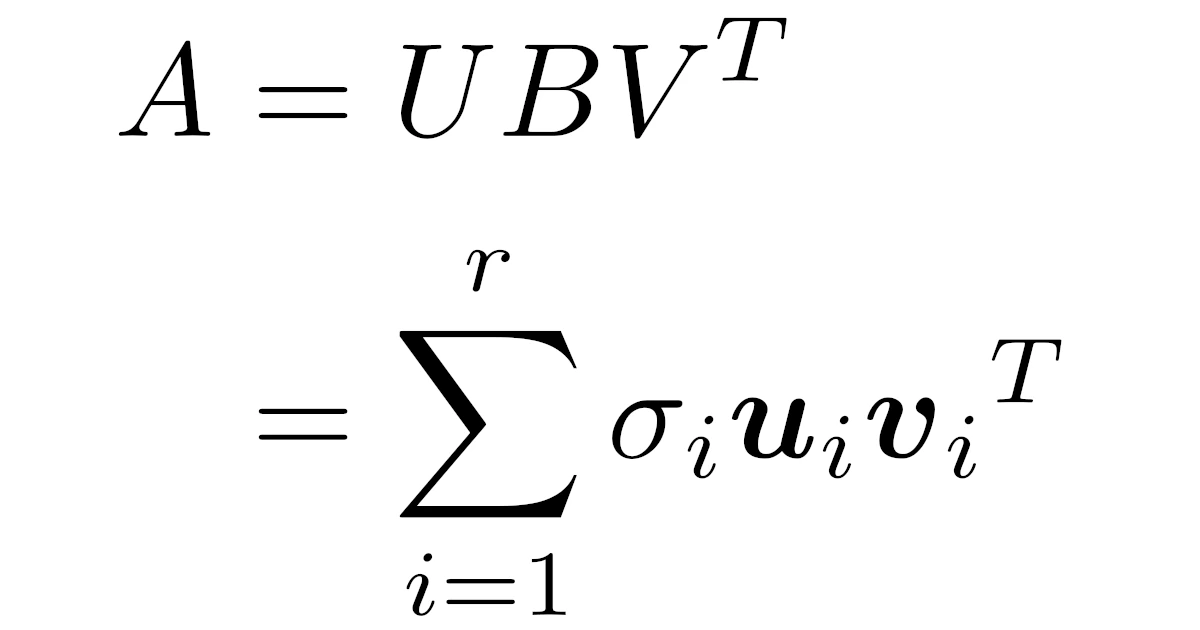
コメント