不偏推定量とは何か？｜標本平均・不偏分散の不偏性も証明

例えば「日本人の成人男性の平均身長」などを考えたいとしても，日本人の成人男性全員の身長を測ることは現実的には不可能なので，ある程度の量のデータを収集して推測することになります．

このように何らかのデータから推測を行う場合には不偏推定量が重要になる場合があります．

不偏推定量とは母集団の平均や分散などの特徴量の「良い」推測ができる標本の統計量の１つで，たとえば分散の不偏推定量として不偏分散というものがあります．

この記事では，不偏推定量の考え方を説明し

母平均の不偏推定量
母分散の不偏推定量

を考えます．

「統計学」の一連の記事

回帰直線

推定
1. e1 不偏分散ってなに？｜不偏推定量を考え方から理解する (今の記事)
2. e2 尤度関数の考え方｜データから分布を推定する最尤推定法の例

推測統計と不偏推定量
1. 推測統計
2. 不偏推定量
母平均と母分散の不偏推定量
1. 母平均の不偏推定量
2. 母分散の不偏推定量
不偏性の証明
1. 標本平均の不偏性
2. 不偏分散の不偏性
参考文献
1. 改訂版統計検定２級対応統計学基礎

推測統計と不偏推定量

考えたい対象の全てのデータを手に入れることができれば良いわけですが，国勢調査など全体のデータが多い場合などでは，当然のことながら全数調査は現実的ではありません．

このようなとき，どのようにして全体の様子を推測するかを考えましょう．

推測統計

いくつかの言葉を確認しておきましょう．

知りたい全てのデータを母集団といい，母集団全てのデータを集めて考えることを全数調査や悉皆調査などという．また，母集団から一部のデータを収集したとき，そのデータを標本という．

例えば，選挙速報などでは

全有権者のデータが母集団
出口調査のデータが標本

ということになりますね．この選挙速報でもそうですが，全量調査が不可能な場合には標本から母集団の様子を推測することになります．

このように，標本から母集団を推測することを総称して推測統計といいます．

例えば，味噌汁を作るとき少しだけ味見をすれば全体の味が推測できます．推測統計はいわばこの味見のようなもので，部分的にデータを収集する（標本を考える）ことで全体の様子を推測しようというものです．

そこで，標本から母集団のだいたい実態が推測できる方法があると嬉しいですね．

不偏推定量

そこで次の問題を考えてみましょう．

母平均を標本から推測するにはどうすれば良いか？

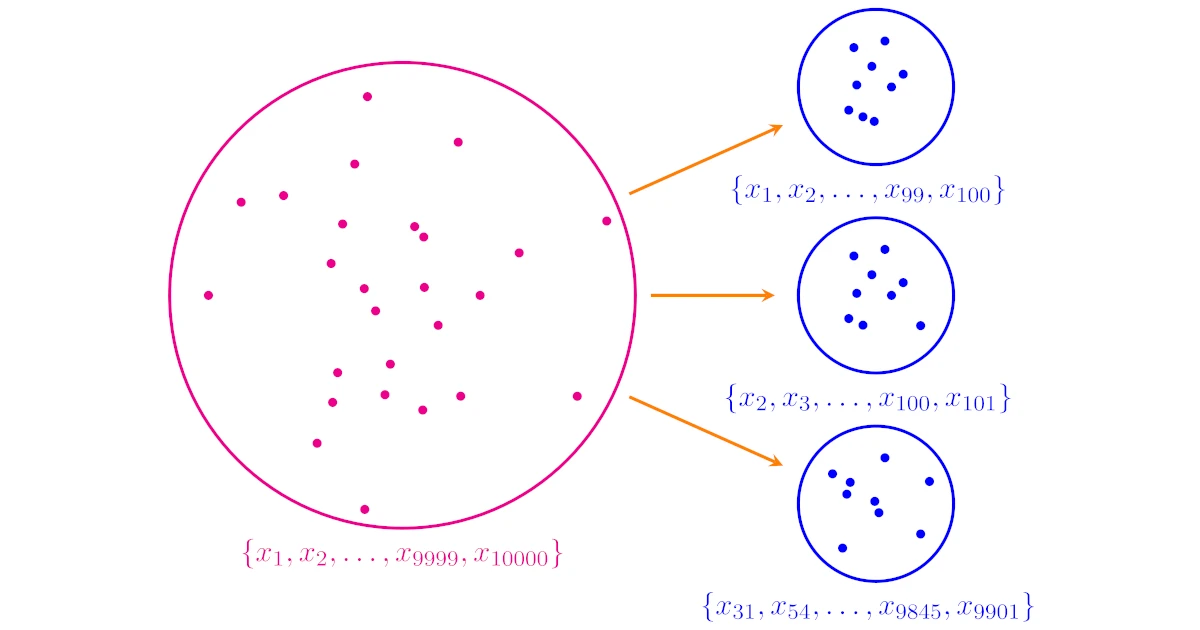
母集団が10000個のデータ$\{x_1,x_2,\dots,x_{9999},x_{10000}\}$からなるとしましょう．

ここから100個のデータからなる標本をとるとき，例えば

$\{x_1,x_2,\dots,x_{99},x_{100}\}$
$\{x_2,x_3,\dots,x_{100},x_{101}\}$
$\{x_{31},x_{54},\dots,x_{9845},x_{9901}\}$

など100個の標本の標本の選び出し方は様々考えられますね．

これらそれぞれの標本平均を考えると，

標本$\{x_1,x_2,\dots,x_{99},x_{100}\}$の平均は$\dfrac{x_1+x_2+\dots+x_{99}+x_{100}}{100}$
標本$\{x_2,x_3,\dots,x_{100},x_{101}\}$の平均は$\dfrac{x_2+x_3+\dots+x_{100}+x_{101}}{100}$
標本$\{x_{31},x_{54},\dots,x_{9845},x_{9901}\}$の平均は$\dfrac{x_{31}+x_{54}+\dots+x_{9845}+x_{9901}}{100}$

となります．

標本をとるたびに得られる値は確率的に変化しますから，１つ１つの標本は確率変数ということができます．

のちに説明するように，実は100個の標本からなる標本たちの「標本平均の平均」は母平均に等しくなり，この性質を「標本平均は母平均の不偏推定量である」といいます．

このように不偏推定量は次のように定義されます．

母集団の統計量$\theta$に対して，無作為標本から推定した統計量$\hat{\theta}$の平均$E[\hat{\theta}]$が$\theta$に等しいとする．すなわち

$\begin{align*}E[\hat{\theta}]=\theta\end{align*}$

が成り立つとする．このとき，$\hat{\theta}$は$\theta$の不偏推定量（unbiased estimator）という．

このように，あらゆる標本の統計量$\hat{\theta}$を考え，それらの平均が母集団の統計量$\theta$に一致しているという性質を不偏性といいます．

不偏推定量は「標本から母集団の統計量を良く推定するもの」ということができますね．

母平均と母分散の不偏推定量

一般に，母集団の平均を母平均，母集団の分散を母分散といいます．ここでは

母平均の不偏推定量として標本平均
母分散の不偏推定量として不偏分散

を紹介します．

母集団のデータ数が多い場合には，非復元抽出でもほとんど復元抽出に等しくなります．そのため，以下では全て復元抽出で考えます．

実際の応用の現場でも母集団が多くのデータからなるときは，厳密には被復元抽出であっても，復元抽出と考えることはよくあります．

母平均の不偏推定量

データの平均は次のように定義されるのでした．

無作為標本$X_1,X_2,\dots,X_n$に対して，

$\begin{align*}\dfrac{X_1+X_2+\dots+X_n}{n}\bra{=\frac{1}{n}\sum_{k=1}^{n}X_k}\end{align*}$

を$X_1,X_2,\dots,X_n$の標本平均という．

一般に標本平均は$\overline{X}$で表すことが多いです．

先ほど軽く触れたように，標本平均は母平均の不偏推定量となります．

母平均を$\mu$とする．無作為標本$X_1,X_2,\dots,X_n$を考えたとき，標本平均$\overline{X}$は

$\begin{align*}E\brc{\overline{X}}=\mu \bra{\iff E\brc{\frac{1}{n}\sum_{k=1}^{n}X_k}=\mu}\end{align*}$

が成り立つ．すなわち，標本平均$\overline{X}$は母平均$\mu$の不偏推定量である．

母分散の不偏推定量

データの分散は次のように定義されるのでした．

無作為標本$X_1,X_2,\dots,X_n$に対して，

$\begin{align*}\dfrac{(X_1-\mu)^2+(X_2-\mu)^2+\dots+(X_n-\mu)^2}{n}\bra{=\frac{1}{n}\sum_{k=1}^{n}(X_k-\mu)^2}\end{align*}$

を$X_1,X_2,\dots,X_n$の標本分散という．ただし，$\overline{X}$は標本平均である．

標本分散は$S^2$や$\hat{\sigma}^2$などで表すことが多いですが，テキストによって使われる記号はまちまちなので注意してください．

さて，平均のときと同様に直感的には「標本分散は母分散の不偏推定量」と思ってしまいそうですが，実は標本分散の平均は母分散とはならず，正しくは次のようになります．

母平均を$\mu$，母分散を$\sigma^2$とする．無作為標本$X_1,X_2,\dots,X_n$（$n\ge2$）を考えたとき，

$\begin{align*}E\brc{\frac{1}{n-1}\sum_{k=1}^{n}(X_k-\overline{X})^2}=\sigma^2\end{align*}$

が成り立つ．すなわち，$\dfrac{1}{n-1}\sum\limits_{k=1}^{n}(X_k-\overline{X})^2$は$\sigma^2$の不偏推定量である．

この

$\begin{align*}\frac{1}{n-1}\sum_{k=1}^{n}(X_k-\overline{X})^2\end{align*}$

を$X_1,X_2,\dots,X_n$の不偏分散（unbiased variance）という．ただし，$\overline{X}$は標本平均である．

標本分散と不偏分散の違いは

標本分散：$n$で割られている
不偏分散：$(n-1)$で割られている

というだけですね．分母が少し小さい不偏分散の方が，標本分散よりも少し大きい値になっています．

不偏性の証明

それでは，いま紹介した標本平均の不偏性と，不偏分散の不偏性を証明しましょう．

標本平均の不偏性

（再掲）母平均を$\mu$とする．無作為標本$X_1,X_2,\dots,X_n$を考えたとき，標本平均$\overline{X}$は

$\begin{align*}E\brc{\overline{X}}=\mu \bra{\iff E\brc{\frac{1}{n}\sum_{k=1}^{n}X_k}=\mu}\end{align*}$

が成り立つ．すなわち，標本平均$\overline{X}$は母平均$\mu$の不偏推定量である．

母平均は$\mu$なので

$\begin{align*}E[X_1]=E[X_2]=\dots=E[X_n]=\mu\end{align*}$

である．標本平均$\overline{X}$は

$\begin{align*}\overline{X}=\frac{X_1+X_2+\dots+X_n}{n}\end{align*}$

なので，

$\begin{align*}E[\overline{X}]&=E\brc{\frac{X_1+X_2+\dots+X_n}{n}} \\&=\frac{1}{n}(E[X_1]+E[X_2]+\dots+E[X_n]) \\&=\frac{1}{n}(\mu+\mu+\dots+\mu)=\mu\end{align*}$

が従う．

不偏分散の不偏性

（再掲）母平均を$\mu$，母分散を$\sigma^2$とする．無作為標本$X_1,X_2,\dots,X_n$（$n\ge2$）を考えたとき，

$\begin{align*}E\brc{\frac{1}{n-1}\sum_{k=1}^{n}(X_k-\mu)^2}=\sigma^2\end{align*}$

が成り立つ．すなわち，不偏分散$\dfrac{1}{n-1}\dsum_{k=1}^{n}(X_k-\mu)^2$は$\sigma^2$の不偏推定量である．

母平均$\mu$，母分散$\sigma^2$だから，各$k\in\{1,2,\dots,n\}$に対して

$\begin{align*}E[X_1]=E[X_2]=\dots=E[X_n]=\mu, V[X_1]=V[X_2]=\dots=V[X_n]=\sigma^2\end{align*}$

である．以下，標本平均を$\overline{X}$とする．

ステップ１（$\sum\limits_{k=1}^{n}(x_k-\overline{X})^2$の計算）

各$(X_k-\overline{X})^2$は

$\begin{align*}(X_k-\overline{X})^2 &=\{(X_k-\mu)+(\mu-\overline{X})\}^2 \\&=(X_k-\mu)^2+2(X_k-\mu)(\mu-\overline{X})+(\mu-\overline{X})^2\end{align*}$

と展開できるから，和を取れば

$\begin{align*}&\sum_{k=1}^{n}(X_k-\overline{X})^2 \\&=\sum_{k=1}^{n}(X_k-\mu)^2+2(\mu-\overline{X})\sum_{k=1}^{n}(x_k-\mu)+n(\mu-\overline{X})^2 \end{align*}$

となる．第２項目について，

$\begin{align*}\sum_{k=1}^{n}(X_k-\mu) &=n\cdot\frac{X_1+X_2+\dots+X_n}{n}-n\mu \\&=n\overline{X}-n\mu =-n(\mu-\overline{X}u)\end{align*}$

なので，

$\begin{align*}&\sum_{k=1}^{n}(X_k-\overline{X})^2 \\&=\sum_{k=1}^{n}(x_k-\mu)^2-2n(\mu-\overline{X})^2+n(\mu-\overline{X})^2 \\&=\sum_{k=1}^{n}(x_k-\mu)^2-n(\mu-\overline{X})^2 \end{align*}$

が従う．

ステップ２（$E\bigl[(X_k-\mu)^2\bigr]$と$E\bigl[(\mu-\overline{X})^2\bigr]$の計算）

$E[X_k]=\mu$だから

$\begin{align*}E[(X_k-\mu)^2]=E[(X_k-E[X_k])^2]=V[X_k]=\sigma^2\end{align*}$

である．

また，先ほど示したように$E[\overline{X}]=\mu$（標本平均$\overline{X}$は母平均$\mu$の不偏推定量）だったから，

$\begin{align*}E\brc{(\mu-\overline{X})^2} &=E\brc{\bra{\overline{X}-E[\overline{X}]}^2}=V[\overline{X}] \\&=V\brc{\frac{1}{n}\sum_{k=1}^{n}x_k}=\frac{1}{n^2}\sum_{k=1}^{n}V[X_k]\end{align*}$

を得る．ただし，最後の等号では$\{X_1,X_2,\dots,X_n\}$が無作為標本であることから，$k\neq\ell$なら$X_k$と$X_\ell$が独立であることを用いている．

$V[X_k]=\sigma^2$と併せて

$\begin{align*}E\brc{(\mu-\overline{X})^2}=\frac{1}{n^2}\sum_{k=1}^{n}\sigma^2=\frac{1}{n^2}\cdot n\sigma^2=\frac{\sigma^2}{n}\end{align*}$

が従う．

ステップ３（$E\brc{\frac{1}{n-1}\sum_{k=1}^{n}(X_k-\overline{X})^2}$の計算）

ステップ１から

$\begin{align*}E\brc{\sum_{k=1}^{n}(X_k-\overline{X})^2} &=E\brc{\sum_{k=1}^{n}(X_k-\overline{X})^2} \\&=E\brc{\sum_{k=1}^{n}(X_k-\mu)^2-n(\mu-\overline{X})^2} \\&=\sum_{k=1}^{n}E\brc{(X_k-\mu)^2}-nE\brc{(\mu-\overline{X})^2}\end{align*}$

である．よって，ステップ２と併せて

$\begin{align*}E\brc{\frac{1}{n-1}\sum_{k=1}^{n}(X_k-\overline{X})^2} &=\frac{1}{n-1}E\brc{\sum_{k=1}^{n}(X_k-\overline{X})^2} \\&=\frac{1}{n-1}\bra{\sum_{k=1}^{n}\sigma^2-n\cdot\frac{\sigma^2}{n}} \\&=\frac{1}{n-1}(n\sigma^2-\sigma^2)=S\end{align*}$