 データの記述
データの記述 共分散から相関の正負が分かる!考え方から定義を理解する
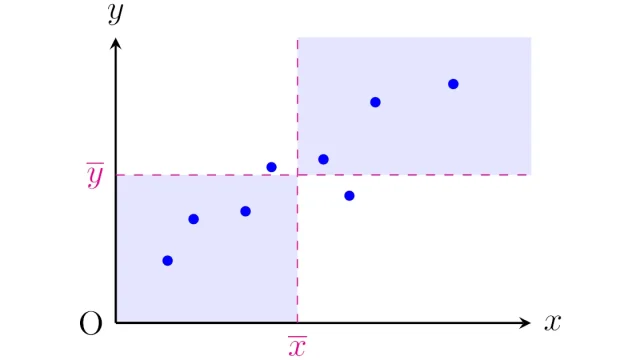
2種類のデータについて,一方が大きいときに他方も大きい傾向があることを「正の相関」があるといい,一方が大きいときに他方が小さい傾向があることを「負の相関」があるといいます.
 データの記述
データの記述 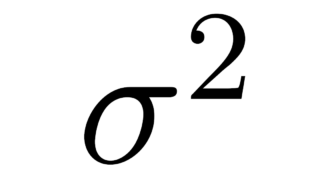 データの記述
データの記述 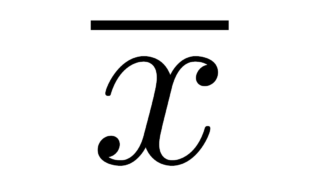 データの記述
データの記述 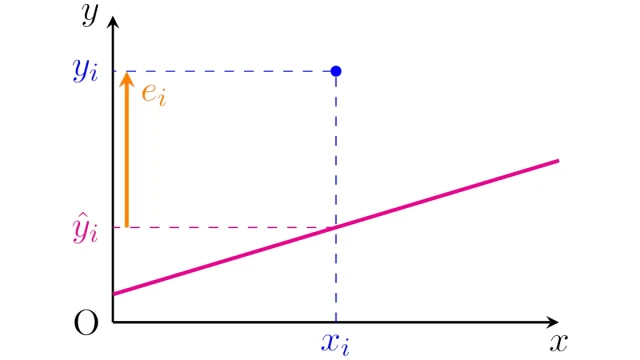 統計学
統計学  統計学
統計学  統計学
統計学 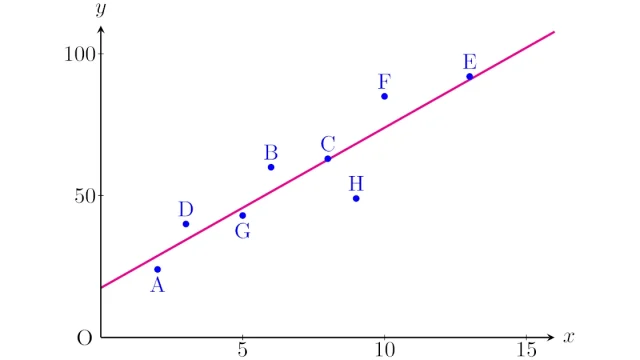 統計学
統計学  統計学
統計学