1日の「プールの利用者数」と「アイスの売り上げ」を記録すると,これらには正の相関があります.
しかし,「プールの利用者数が多くなるからアイスの売り上げが上がる」わけではないし,逆に「アイスの売り上げが上がるからプールの利用者数が多くなる」わけでもありません.
このように,相関とはあくまで「片方が大きいときに他方も大きいかどうか」を考えるものなので,どちらかが原因でどちらかが結果という因果関係までは教えてくれません.
そこで,なぜ「プールの利用者数」と「アイスの売り上げ」にそう考えるのかを考えると,共通の原因として「気温」が挙げられるためですね.
この「プールの利用者数」と「アイスの売り上げ」のように,因果関係がないのに相関があることを擬似相関といいます.
そこで,「気温」の変化による「プールの利用者数」と「アイスの売り上げ」の影響を除いたものの相関を考えると,相関関係は見られないのではないかと予想ができます.
このように,ある特定の影響を除いて考える相関係数のことを偏相関係数といいます.
この記事では
- 偏相関係数の考え方と定義
- 偏相関係数の定義と導出
を順に説明します.
「統計学」の一連の記事
偏相関係数の考え方と定義
回帰直線の復習をしてから偏相関係数の考え方と定義を説明します.
回帰直線の復習
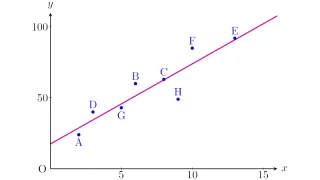
例えば,あるテストを受けた8人の生徒について,勉強時間$x$とテストの成績$y$を散布図にして下図のようになったとしましょう.
この散布図を見たとき,データはなんとなく右上がりになっているように見えるので,このデータを直線で表すなら下図のようになるでしょうか.
回帰分析でデータを表現する線は必ずしも直線とは限らず,曲線であることもありますが,「それっぽい線」を見つける方法の総称を回帰分析といいますね.
とくにデータの間に直線関係があるとして考えた「それっぽい直線」を回帰直線といい,回帰直線を求めるための手法として最小二乗法などがあります.
最小二乗法を用いて回帰直線を求めると以下のようになります.
$n$個のデータの組$x=(x_1,x_2,\dots,x_n)$, $y=(y_1,y_2,\dots,y_n)$に対して最小二乗法を用いると,回帰直線は
\begin{align*}y=\hat{a}+\hat{b}x\quad
\bra{\hat{b}=\frac{C_{xy}}{{\sigma_x}^2},\quad
\hat{a}=\bar{y}-\hat{b}\bar{x}}\end{align*}
となる.ただし,$\bar{x}$は$x$の平均,${\sigma_x}^2$は$x$の分散,$\bar{y}$は$y$の平均,$C_{xy}$は$x$, $y$の共分散である.
この回帰直線の導出は以下の記事で詳しく説明しています.
偏相関係数
冒頭で説明したように,相関が強いことは必ずしも因果関係があることを意味しません.例えば
- プールの利用者数
- アイスの売り上げ
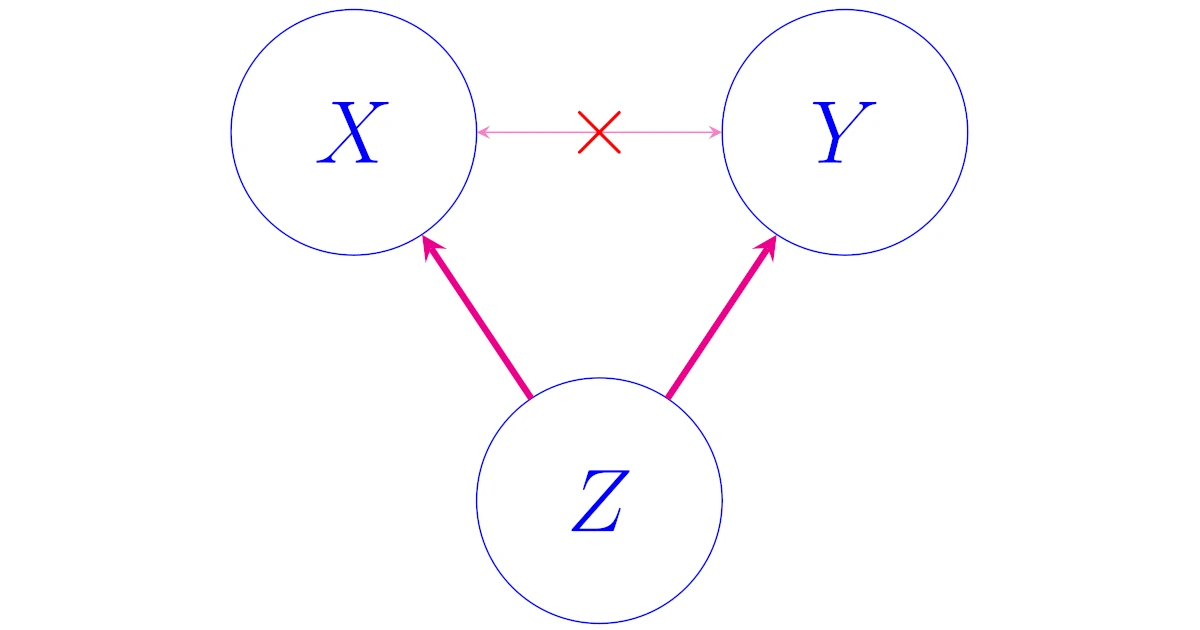
に相関はありますが,一方が他方の原因になっているわけではありません.これは両方に影響を与える「気温」という要因があるため,相関があるだけですね.
このように,何らかの分析をしていてデータ$X$と$Y$を見比べて正の相関が見つかったとしても,$X$と$Y$に影響を与える別の要因$Z$が存在しているだけかもしれないず,「$Y$を増やしたいから,$X$を増やせばいい」と考えることは危険です.
このように,$X$と$Y$が相関関係にあっても,因果関係にないことを擬似相関などといいます.
さて,$x$と$y$の間に直接的な関係があるのかどうかをみるための指標として,($z$の影響を除いた)偏相関係数というものがあります.これは
- $x$から$z$の影響を除いた$x’$
- $y$から$z$の影響を除いた$x’$
の相関係数$\rho_{x’y’}$のことで,$z$の影響を除いた$x’$と$y’$の間に相関があれば,$z$の影響だけではない関係があると見なすことができますね.
結論から書けば,偏相関係数は以下のように定義されます.
[偏相関係数]データ$x=(x_1,\dots,x_n)$, $y=(y_1,\dots,y_n)$, $z=(z_1,\dots,z_n)$に対して,$z$の影響を除いた$x$と$y$の偏相関係数$\rho_{xy;z}$を
\begin{align*}\rho_{xy;z}:=\frac{\rho_{xy}-\rho_{xz}\rho_{yz}}{\sqrt{1-{\rho_{xz}}^2}\sqrt{1-{\rho_{yz}}^2}}\end{align*}
で定義する.
偏相関係数の導出
それでは,偏相関係数はなぜ定義のような形になるのか導出しましょう.
データ$x=(x_1,\dots,x_n)$, $y=(y_1,\dots,y_n)$, $z=(z_1,\dots,z_n)$について,$x$と$z$は直線関係にあり,$y$と$z$は直線関係にあるとし,$x$と$z$の回帰直線,$y$と$z$の回帰直線をそれぞれ
- $x=\hat{a}+\hat{b}z$
- $y=\hat{c}+\hat{d}z$
とする.このとき,$z$の影響を無視した$x$と$y$をそれぞれ
- $x’=x-(\hat{a}+\hat{b}z)$
- $y’=y-(\hat{c}+\hat{d}z)$
で定義すると,$x’$と$y’$の相関係数$\rho_{x’y’}$は偏相関係数$\rho_{xy;z}$に一致する.すなわち,
\begin{align*}\rho_{x’y’}=\frac{\rho_{xy}-\rho_{xz}\rho_{yz}}{\sqrt{1-{\rho_{xz}}^2}\sqrt{1-{\rho_{yz}}^2}}\end{align*}
先ほど
- $x$から$z$の影響を除いた$x’$
- $y$から$z$の影響を除いた$y’$
の相関係数$\rho_{x’y’}$が偏相関係数$\rho_{xy;z}$であると書きましたが,正確には偏相関係数$\rho_{xy;z}$は「$x$と$z$,$y$と$z$が直線関係にあるとしたときの,$z$の影響を無視した$x$と$y$の相関係数」が偏相関係数ということになります.
上で見た回帰直線の復習から
\begin{align*}&\hat{b}=\dfrac{C_{xz}}{{\sigma_{z}}^2},\quad
\hat{a}=\bar{x}-\hat{b}\bar{z},\\
&\hat{d}=\dfrac{C_{yz}}{{\sigma_{z}}^2},\quad
\hat{c}=\bar{y}-\hat{b}\bar{z}\end{align*}
ですね.これを用いて相関係数$\rho_{x’y’}$を変形していきましょう.
相関係数$\rho_{x’y’}$の変形
$\hat{a}=\bar{x}-\hat{b}\bar{z}$より
\begin{align*}x’&=x-(\hat{a}+\hat{b}z)
\\&=x-\brb{(\bar{x}-\hat{b}\bar{z})+\hat{b}z}
\\&=(x-\bar{x})-\hat{b}(z-\bar{z})\end{align*}
であり,同様に$y’=(y-\bar{y})-\hat{d}(z-\bar{z})$です.
また,共分散$C_{x’y’}$,標準偏差$\sigma_{x’}$, $\sigma_{y’}$は
\begin{align*}&C_{x’y’}=\overline{x’y’}-\overline{x’}\overline{y’},
\\&{\sigma_{x’}}^2=\overline{x’^2}-\overline{x’}^2,
\\&{\sigma_{y’}}^2=\overline{y’^2}-\overline{y’}^2\end{align*}
を満たすので,相関係数の定義より
\begin{align*}\rho_{x’y’}=&\frac{C_{x’y’}}{\sigma_{x’}\sigma_{y’}}
\\=&\frac{\overline{x’y’}-\overline{x’}\cdot\overline{y’}}{\sqrt{\overline{x’^2}-\overline{x’}^2}\sqrt{\overline{y’^2}-\overline{y’}^2}}\end{align*}
となります.よって,以下で
\begin{align*}\overline{x’},\quad
\overline{y’},\quad
\overline{x’^2},\quad
\overline{y’^2},\quad
\overline{x’y’}\end{align*}
を計算して上の式に代入することで$\rho_{x’y’}$を求めましょう.
$x’$と$y’$の計算
$x’=(x-\bar{x})-\hat{b}(z-\bar{z})$なので,
\begin{align*}\overline{x’}&=\frac{1}{n}\sum_{i=1}^{n}x’_i
=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})-\hat{b}(z_i-\bar{z})
\\&=\brb{\bra{\frac{1}{n}\sum_{i=1}^{n}x_i}-\bar{x}}-\hat{b}\brb{\bra{\frac{1}{n}\sum_{i=1}^{n}z_i}-\bar{z}}
\\&=(\bar{x}-\bar{x})-\hat{b}(\bar{z}-\bar{z})=0\end{align*}
となります.同様に,$\overline{y’}=0$となります.
$\overline{x’^2}$と$\overline{y’^2}$の計算
$x’=(x-\bar{x})-\hat{b}(z-\bar{z})$より
\begin{align*}x’^2&=\brb{(x-\bar{x})-\hat{b}(z-\bar{z})}^2
\\&=(x-\bar{x})^2-2\hat{b}(x-\bar{x})(z-\bar{z})+\hat{b}^2(z-\bar{z})^2\end{align*}
となるので,$\hat{b}=\dfrac{C_{xz}}{{\sigma_{z}}^2}$と併せて
\begin{align*}\overline{x’^2}&=\frac{1}{n}\sum_{i=1}^{n}{x’_i}^2
\\&=\frac{1}{n}\sum_{i=1}^{n}\brb{(x_i-\bar{x})^2-2\hat{b}(x_i-\bar{x})(z_i-\bar{z})+\hat{b}^2(z_i-\bar{z})^2}
\\&=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2-2\hat{b}\cdot\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})(z_i-\bar{z})+\hat{b}^2\cdot\frac{1}{n}\sum_{i=1}^{n}(z_i-\bar{z})^2
\\&={\sigma_{x}}^2-2\hat{b}\cdot C_{xz}+\hat{b}^2\cdot{\sigma_{z}}^2
\\&={\sigma_{x}}^2-2\cdot\frac{C_{xz}}{{\sigma_{z}}^2}\cdot C_{xz}+\frac{{C_{xz}}^2}{{\sigma_{z}}^4}\cdot{\sigma_{z}}^2
\\&={\sigma_{x}}^2-\frac{2{C_{xz}}^2}{{\sigma_{z}}^2}+\dfrac{{C_{xz}}^2}{{\sigma_{z}}^2}
\\&={\sigma_{x}}^2-\frac{{C_{xz}}^2}{{\sigma_{z}}^2}\end{align*}
となります.同様に$\overline{y’^2}={\sigma_{y}}^2-\dfrac{{C_{yz}}^2}{{\sigma_{z}}^2}$となります.
$\overline{x’y’}$の計算
$x’=(x-\bar{x})-\hat{b}(z-\bar{z})$, $y’=(y-\bar{y})-\hat{d}(y-\bar{y})$より
\begin{align*}x’y’&=\brb{(x-\bar{x})-\hat{b}(z-\bar{z})}\brb{(y-\bar{y})-\hat{d}(z-\bar{z})}
\\&=(x-\bar{x})(y-\bar{y})-\hat{d}(x-\bar{x})(z-\bar{z})
\\&\quad-\hat{b}(y-\bar{y})(z-\bar{z})+\hat{b}\hat{d}(z-\bar{z})^2\end{align*}
となるので,$\hat{b}=\dfrac{C_{xz}}{{\sigma_z}^2}$, $\hat{d}=\dfrac{C_{yz}}{{\sigma_z}^2}$と併せて
\begin{align*}\overline{x’y’}&=\frac{1}{n}\sum_{i=1}^{n}x’_ix’_i
\\&=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})-\hat{d}\cdot\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})(z_i-\bar{z})
\\&-\hat{b}\cdot\frac{1}{n}\sum_{i=1}^{n}(y_i-\bar{y})(z_i-\bar{z})+\hat{b}\hat{d}\cdot\frac{1}{n}\sum_{i=1}^{n}(z_i-\bar{z})^2
\\&=C_{xy}-\hat{d}\cdot C_{xz}-\hat{b}\cdot C_{yz}+\hat{b}\hat{d}\cdot{\sigma_{z}}^2
\\&=C_{xy}-\frac{C_{yz}}{{\sigma_z}^2}\cdot C_{xz}-\frac{C_{xz}}{{\sigma_z}^2}\cdot C_{yz}+\frac{C_{xz}}{{\sigma_z}^2}\cdot\frac{C_{yz}}{{\sigma_z}^2}\cdot{\sigma_z}^2
\\&=C_{xy}-\frac{C_{xz}C_{yz}}{{\sigma_z}^2}-\frac{C_{xz}C_{yz}}{{\sigma_z}^2}+\frac{C_{xz}C_{yz}}{{\sigma_z}^2}
\\&=C_{xy}-\frac{C_{xz}C_{yz}}{{\sigma_z}^2}\end{align*}
となります.
相関係数$\rho_{x’y’}$と偏相関係数$\rho_{xy;z}$
以上より,
\begin{align*}\rho_{x’y’}&=\frac{\overline{x’y’}-\overline{x’}\cdot\overline{y’}}{\sqrt{\overline{x’^2}-\overline{x’}^2}\sqrt{\overline{y’^2}-\overline{y’}^2}}
\\&=\frac{\bra{C_{xy}-\frac{C_{xz}C_{yz}}{{\sigma_z}^2}}-0\cdot0}{\sqrt{\bra{{\sigma_x}^2-\frac{{C_{xz}}^2}{{\sigma_z}^2}}-0^2}\sqrt{\bra{{\sigma_y}^2-\frac{{C_{yz}}^2}{{\sigma_{z}}^2}}-0^2}}
\\&=\frac{C_{xy}-\frac{C_{xz}C_{yz}}{{\sigma_z}^2}}{\sqrt{{\sigma_x}^2-\frac{{C_{xz}}^2}{{\sigma_z}^2}}\sqrt{{\sigma_{y}}^2-\frac{{C_{yz}}^2}{{\sigma_z}^2}}}
\\&=\frac{\frac{C_{xy}}{\sigma_x\sigma_y}-\frac{C_{xz}}{\sigma_x\sigma_z}\cdot\frac{C_{yz}}{\sigma_y\sigma_z}}{\sqrt{1-\bra{\frac{C_{xz}}{\sigma_x\sigma_z}}^2}\sqrt{1-\bra{\frac{C_{yz}}{\sigma_y\sigma_z}}^2}}
\\&=\frac{\rho_{xy}-\rho_{xz}\rho_{yz}}{\sqrt{1-{\rho_{xz}}^2}\sqrt{1-{\rho_{yz}}^2}}=\rho_{xy;z}\end{align*}
となって,$x’$と$y’$の相関$\rho_{x’y’}$が偏相関係数$\rho_{xy;z}$に等しいことが分かりました.
参考文献
以下は参考文献
統計学
[久保川達也 著/東京大学出版会]
現代の統計学は社会学・心理学・機械学習など様々な分野に応用されている極めて実学的な分野です.
本書は統計学の基礎を基礎から丁寧に解説した初学者向けのテキストで,大きく
- 第1部:統計データの整理と記述のための基礎事項
- 第2部:統計学で必要となる確率の知識
- 第3部:統計的推測の基礎事項
- 第4部:社会・経済・時系列データ
の4部構成になっています(本書「はしがき」より).
著者が大学2年生に向けて行った講義に基づいて書かれており,数理的な計算はしっかり追いつつも分かりやすさを重視した記述になっています.
難易度としては統計検定の2級を少し超えたくらいになっており,部分的には準1級レベルの箇所もあります.
章末問題も豊富にあり,統計検定の2級対策としても利用できます.
さらに,著者による章末問題の略解がウェブにアップロードされているのも独学者にはありがたい点です.
改訂版 統計検定2級対応 統計学基礎
[日本統計学会 編/東京図書]
統計検定2級は「大学基礎科目(学部1,2年程度)としての統計学の知識と問題解決能力」という位置付けであり,ある程度の数学的な処理能力が求められます.
そのため,統計検定2級を取得していると,一定以上の統計的なデータの扱い方を身に付けているという指標になります.
日本統計学会が実施する「統計検定」の2級の範囲に対応する教科書なので,「2級の試験範囲を確認する」くらいのつもりで持っておくのが良いかもしれません.
しかし,このテキストは表面的な説明に留まっているなど読みづらい部分も多いので,本書だけで2級の対策をするのは少し難しいと思います.
大学1年の微分積分学の知識は必要なので,もし自信がなければ統計検定3級からの挑戦を検討しても良いでしょう.
なお,本書については,以下の記事で書評としてまとめています.
【教科書紹介|統計検定2級対応 統計学基礎(日本統計学会編)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.



コメント