最小二乗法から求めた回帰直線の性質と決定係数の意味

「気温」と「アイスの売り上げ」のような２つの関連するデータを散布図として表し，その関係を「それっぽい直線や曲線」で表すことを回帰分析というのでした．

この回帰分析における「それっぽい直線」のことを回帰直線といい，回帰直線を求める際には最小二乗法がよく用いられます．

さて，最小二乗法により求まった回帰直線がどれくらい「それっぽい」のかを表す指標に決定係数というものがあり，決定係数は

１に近いほど精度の良い回帰直線
０に近いほど精度の悪い回帰直線

になっていると判断できるものになっています．

この記事では

回帰直線の復習
回帰直線の性質
平方和の分解と決定係数

を順に説明します．

「統計学」の一連の記事

基本の統計量

回帰直線

推定
1. e1 不偏分散ってなに？｜不偏推定量を考え方から理解する
2. e2 尤度関数の考え方｜データから分布を推定する最尤推定法の例

回帰直線の復習
回帰直線の性質
平方和の分解と決定係数
1. 平方和の分解
2. 決定係数
参考文献
1. 改訂版統計検定２級対応統計学基礎

回帰直線の復習

最小二乗法により求められる回帰直線は以下のようになるのでした．

$n$個のデータの組$x=(x_1,x_2,\dots,x_n)$, $y=(y_1,y_2,\dots,y_n)$に対して，最小二乗法を用いると回帰直線は

$\begin{align*}y=\hat{a}+\hat{b}x\quad \bra{\hat{b}=\frac{C_{xy}}{{\sigma_x}^2},\quad \hat{a}=\overline{y}-\hat{b}\overline{x}}\end{align*}$

となる．

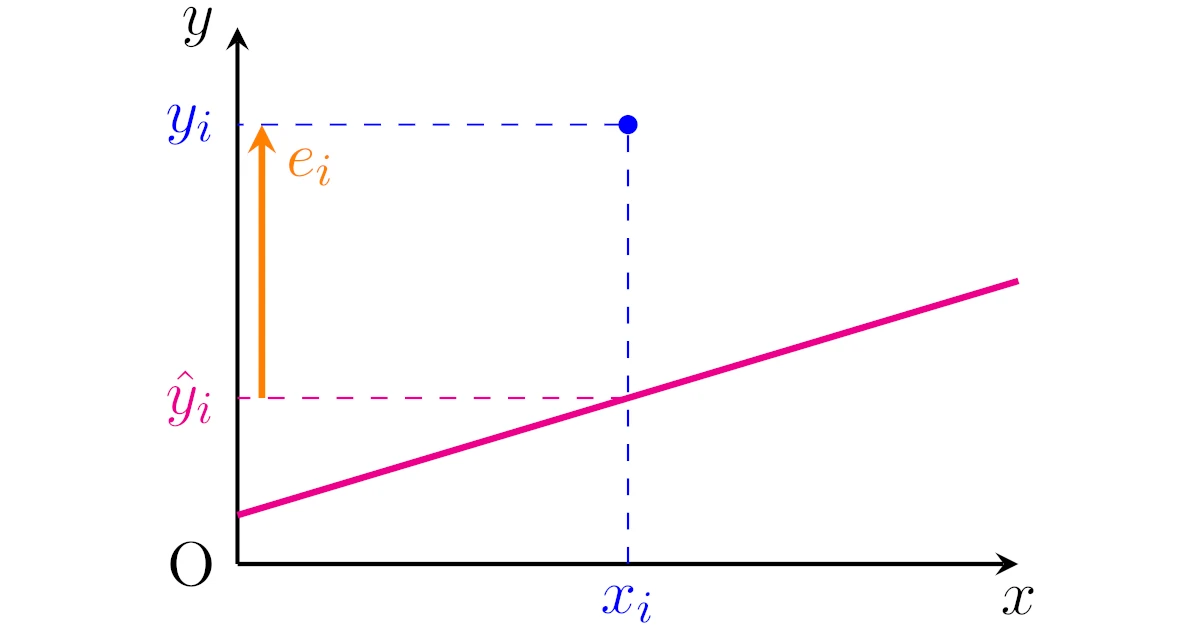
$\overline{x}$は$x$の平均，${\sigma_x}^2$は$x$の分散，$\overline{y}$は$y$の平均，$C_{xy}$は$x$, $y$の共分散です．

実際に得られたデータ$(x_i,y_i)$と回帰直線に対して，

$x=x_i$での回帰直線上の$y$の値をデータを$x_i$の予測値
$y_i-\hat{y}_i$をデータ$(x_i,y_i)$の残差

というのでした．この記事では$x_i$の予測値を$\hat{y}_i$と表し，データ$(x_i,y_i)$の残差を$e_i$と表します．

標語的には残差は「（データ）ー（予測値）」です．

回帰直線の性質

最小二乗法で求めた回帰直線は次の性質を満たします．

$n$個のデータの組$x=(x_1,x_2,\dots,x_n)$, $y=(y_1,y_2,\dots,y_n)$に対する最小二乗法による回帰直線$y=\hat{a}+\hat{b}x$は以下の性質をもつ．

回帰直線は点$(\overline{x},\overline{y})$を通る．
予測値$\hat{y}_i$の平均$\overline{\hat{y}}$と$y_i$の平均$\overline{y}$は等しい．すなわち，残差$e_i$の平均$\overline{e}$は0である．
予測値$\hat{y}_i$と残差$e_i$は無相関（相関係数が０，共分散が０）である．

性質１の証明

回帰直線の式$y=\hat{a}+\hat{b}x$では，等式$\hat{a}=\overline{y}-\hat{b}\overline{x}$が成り立つのでした．

これを整理してできる等式$\bar{y}=\hat{a}+\hat{b}\bar{x}$は回帰直線の方程式$y=\hat{a}+\hat{b}x$に$(x,y)=(\bar{x},\bar{y})$を代入してできる等式となっています．

そもそも方程式に代入して成り立つ点$(x,y)$を集めたものがグラフだったので，回帰直線$y=\hat{a}+\hat{b}x$は点$(\bar{x},\bar{y})$を通ることになります．

性質２の証明

予測値$\hat{y}_i$は$\hat{y}_i=\hat{a}+\hat{b}x_i$だったので，

$\begin{align*}\overline{\hat{y}} &=\frac{1}{n}\sum_{i=1}^{n}\hat{y}_i =\frac{1}{n}\sum_{i=1}^{n}(\hat{a}+\hat{b}x_i) \\&=\hat{a}+\hat{b}\cdot\frac{1}{n}\sum_{i=1}^{n}x_i =\bra{\hat{a}+\hat{b}\overline{x}} =\overline{y}\end{align*}$

が成り立ちます．残差$e_i$は$e_i=y_i-\hat{y}_i$と定義されていたので，残差の平均$\overline{e}$は

$\begin{align*}\overline{e} &=\frac{1}{n}\sum_{i=1}^{n}e_i =\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y}_i) \\&=\frac{1}{n}\sum_{i=1}^{n}y_i-\frac{1}{n}\sum_{i=1}^{n}\hat{y}_i =\overline{y}-\overline{\hat{y}}=0\end{align*}$

となりますね．ただし，最後の等号では等式$\overline{y}=\hat{a}+\hat{b}\overline{x}$が成り立つことを用いました．

性質３の証明

予測値$\hat{y}_i$と残差$e_i$の共分散$C_{\hat{y}e}$が０であることを示せばよいですね．

$\begin{align*}e_i&=(y_i-\hat{y}_i) =y_i-(\hat{a}+\hat{b}x_i) \\&=y_i-\brb{(\overline{y}-\hat{b}\overline{x})+\hat{b}x_i} \\&=(y_i-\overline{y})-\hat{b}(x_i-\overline{x})\end{align*}$

なので，性質２の$\bar{\hat{y}}=\bar{y}$と$\bar{e}=0$を併せると

$\begin{align*}C_{\hat{y}e}&=\frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i-\overline{\hat{y}})(e_i-\overline{e}) =\frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i-\overline{y})e_i \\&=\frac{1}{n}\sum_{i=1}^{n}\{(\hat{a}+\hat{b}x_i)-(\hat{a}+\hat{b}\overline{x})\}e_i =\frac{\hat{b}}{n}\sum_{i=1}^{n}(x_i-\overline{x})e_i \\&=\hat{b}\brb{\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})-\hat{b}\cdot\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^2} \\&=\hat{b}\bra{C_{xy}-\hat{b}{\sigma_{x}}^2} =\hat{b}\bra{C_{xy}-\frac{C_{xy}}{{\sigma_{x}}^2}\cdot{\sigma_{x}}^2}=0\end{align*}$

が得られますね．

平方和の分解と決定係数

そもそも回帰分析はデータの関係を表す「それっぽい線」を見つけようというのが目的なのでした．

そこで，最小二乗法で求まった回帰直線がどれくらい「それっぽいか」を測る指標として決定係数があります．

平方和の分解

上で証明した回帰直線の性質３を用いると，以下のことが証明できます．

最小二乗法による回帰直線において，

$\begin{align*}&S_T=\sum_{i=1}^{n}(y_i-\overline{y})^2, \\&S_R=\sum_{i=1}^{n}(\hat{y}_i-\overline{y})^2, \\&S_e=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2\bra{=\sum_{i=1}^{n}{e_i}^2}\end{align*}$

とおくと$S_T=S_e+S_R$が成り立つ．$S_T$を総平方和，$S_e$を残差平方和，$S_{R}$を回帰による平方和という．

上で証明した回帰直線の性質３より，

$\begin{align*}\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y}_i)(\hat{y}_i-\overline{y}) &=\frac{1}{n}\sum_{i=1}^{n}e_i(\hat{y}_i-\overline{\hat{y}_i}) \\&=\frac{1}{n}\sum_{i=1}^{n}(e_i-\overline{e})(\hat{y}_i-\overline{\hat{y}_i})=0\end{align*}$

なので，

$\begin{align*}S_T&=\sum_{i=1}^{n}(y_i-\overline{y})^2 =\sum_{i=1}^{n}\brb{(y_i-\hat{y}_i)+(\hat{y}_i-\overline{y})}^2 \\&=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2+\sum_{i=1}^{n}(\hat{y}_i-\overline{y})^2+\sum_{i=1}^{n}(y_i-\hat{y}_i)(\hat{y}_i-\overline{y}) \\&=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2+\sum_{i=1}^{n}(\hat{y}_i-\overline{y})^2 =S_e+S_R\end{align*}$

となります．

この平方和に関する等式$S_T=S_e+S_R$を平方和の分解といいます．

決定係数

さて，もし全てのデータが回帰直線上にぴったり乗っていれば，データ$y_i$と予測値$\hat{y}_i$が一致しているので残差$e_i$は全て０ですから，残差平方和$S_e$は０となります．

よって，回帰直線がデータの相関を表せているほど残差平方和$S_e$は０に近付き，回帰直線からデータが離れているほど残差平方和$S_e$は$S_T$に近付きます．

平方和の分解$S_T=S_e+S_R$に注意すると，$S_e$が０に近付くほど回帰による平方和$S_R$は$S_T$に近付き，$S_e$が$S_T$に近付くほど$S_R$は０に近付くことが分かります．

このことから，$\dfrac{S_R}{S_T}$の値を考えれば，回帰直線がどれくらい「それっぽい」かを判断することができますね．

目的変数の平均とデータの差の平方和$S_T$と残差平方和$S_R$の比$\dfrac{S_R}{S_T}$を決定係数という．

「決定係数」という言葉を用いて上のことを説明すると，

決定係数が１に近いほど回帰直線の精度が良い
決定係数が０に近いほど回帰直線の精度が悪い

と言えるわけですね．

平方和の分解$S_T=S_e+S_R$について，$S_e\ge0$かつ$S_R\ge0$なので$0\le\dfrac{S_R}{S_T}\le1$はいつでも成り立ちます．

参考文献

改訂版統計検定２級対応統計学基礎

[日本統計学会編/東京図書]

統計検定２級は「大学基礎科目(学部１，２年程度）としての統計学の知識と問題解決能力」という位置付けであり，ある程度の数学的な処理能力が求められます．

そのため，統計検定２級を取得していると，一定以上の統計的なデータの扱い方を身に付けているという指標になります．

日本統計学会が実施する「統計検定」の２級の範囲に対応する教科書なので，「２級の試験範囲を確認する」くらいのつもりで持っておくのが良いかもしれません．

しかし，このテキストは表面的な説明に留まっているなど読みづらい部分も多いので，本書だけで2級の対策をするのは少し難しいと思います．

大学１年の微分積分学の知識は必要なので，もし自信がなければ統計検定３級からの挑戦を検討しても良いでしょう．

改訂版統計検定２級対応統計学基礎(日本統計学会編/東京図書)
Amazon 楽天市場
改訂版統計検定３級対応データの分析(日本統計学会編/東京図書)
Amazon 楽天市場

なお，本書については，以下の記事で書評としてまとめています．

【教科書紹介｜統計検定２級対応統計学基礎(日本統計学会編)】

本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています．

決定係数の意味｜最小二乗法から求めた回帰直線の性質

回帰直線の復習