代数学の基礎となる分野のひとつに群論（group theory）が挙げられます．
群論はその名の通り群を扱う分野のことで，群とはある性質を満たす集合と演算の組のことをいいます．
例えば，群の例としては
- 整数全部の集合$\Z$で足し算$+$を考えたもの
- 正の実数全部の集合$\R_{+}$で掛け算$\times$を考えたもの
- 実数成分の２次正則行列全部の集合$\mrm{GL}_2(\R)$で掛け算$\times$を考えたもの
などが挙げられます．
この記事では
- 群の定義
- 群の具体例
- 単位元と逆元の一意性
- 演算の記法$+$と$\cdot$の使い分け
を順に解説します．
「群論の基本」の一連の記事
- 群と部分群
- 1 群の定義・考え方を具体例から解説 (今の記事)
- 2 部分群の証明のテンプレを例題から理解する
- 生成される部分群・巡回群の定義と具体例(準備中)
- 剰余類とラグランジュの定理｜部分群の位数(準備中)
- 可換群の剰余群を具体例から丁寧に理解する(準備中)
- 正規部分群は非可換群の剰余群で超重要(準備中)
- 群の準同型
- 群の準同型は群の演算を保つ大切な写像(準備中)
- 群の準同型の像Im(f)と核Ker(f)の定義と例題(準備中)
- 群の準同型定理の考え方を例題から掴む(準備中)
群の定義
整数全部の集合$\Z$は足し算$+$について，次の３性質を満たすことは皆さんよくご存知です．
- 任意の$m,n,\ell\in\Z$に対して$(m+n)+\ell=m+(n+\ell)$が成り立つ
- $0\in\Z$は任意の$n\in\Z$に対して$0+n=n+0=n$が成り立つ
- 任意の$n\in\Z$に対して$n+(-n)=(-n)+n=0$が成り立つ
実はこれらと同様の３性質を満たす集合と演算を併せて群と呼びます．のちに定義しますが，いまの場合は「組$(\Z,+)$は群である」といいます．
演算の定義
群の定義のためには演算を定義しておく必要があります．
大雑把に言えば，集合$A$の２つの元から集合$A$の１つの元を作り出す規則を演算といいます．
集合$A$に対して，$A$の元を２つ与えて$A$の元をただ１つ返す規則を二項演算または単に演算という．
また「演算を$\star$とする」と書いた場合は，$a,b\in A$の$\star$による演算の結果を$a\star b$と表す．
正確に書くなら，（二項）演算とは写像$A\times A\to A$のことですね．
例えば，$\Z$上の足し算$+$は
のように，２つの$m,n\in\Z$から新しい別の$\Z$の元を作り出す規則になっています．
これは上の演算の定義の$A=\Z$, $\star=+$の場合になっているので，$\Z$上の足し算$+$は$\Z$上の演算だと言えますね．
群の定義
集合と演算が［結合法則］［単位元の存在］［逆元の存在］を満たすとき，これら併せて群と呼びます．
集合$G$と$G$上の演算$\star$が次の３性質を満たすとき，組$(G,\star)$を群（group）という．
- ［結合法則］任意の$g,h,i\in G$に対して$(g\star h)\star i=g\star (h\star i)$が成り立つ
- ［単位元の存在］ある$e\in G$が存在して，任意の$g\in G$に対して$e\star g=g\star e=g$が成り立つ
- ［逆元の存在］任意の$g\in G$に対して，ある$h\in G$が存在して$g\star h=h\star g=e$が成り立つ（$e$は(2)のもの）
また(2)の$e$を$G$の単位元（identity element）と呼び，(3)の$h$を$g$の逆元（inverse element）と呼ぶ．
具体例のあとで単位元$e$がひとつしか存在しないこと，任意の元に対して逆元がひとつしか存在しないことを証明します．
単位元は全ての元に対して$e\star g=g\star e=g$を満たさなければなりませんが，逆元は$g\in G$ごとに決まることに注意してください．
例えば，先ほど考えたように$(\Z,+)$は群となります．この群の単位元は$0$であり，全ての$n\in\Z$に対して$n+0=0+n$を満たす万能な元です．
一方，$2,-5\in\Z$の逆元はそれぞれ$-2,5$であり，このように元ごとに逆元が決まりますね．
可換群の定義
群$(G,\star)$がさらに［交換法則］を満たすとき，群$(G,\star)$を可換群と呼びます．
群$(G,\star)$が
［交換法則］任意の$g,h\in G$に対して$g\star h=h\star g$が成り立つ
を満たすとき，群$(G,\star)$を可換群（commutative group）またはアーベル群（abelian group）であるという．
群$(\Z,+)$の演算（足し算）$+$が［交換法則］を満たすので，群$(\Z,+)$は可換群ですね．
群の具体例
いくつか群の具体例を紹介します．
例１（可換群$(\Z,+)$）
整数全部の集合$\Z$と通常の足し算$+$の組$(\Z,+)$が可換群であることを示せ．
３つの性質
- ［結合法則］任意の$m,n,\ell\in\Z$に対して$(m+n)+\ell=m+(n+\ell)$が成り立つ
- ［単位元の存在］任意の$n\in\Z$に対して$0+n=n+0=n$が成り立つ
- ［逆元の存在］任意の$n\in\Z$に対して$n+(-n)=(-n)+n=0$が成り立つ
を満たすから組$(\Z,+)$は群である（単位元は$0$で，$n\in\Z$の逆元は$-n$）．さらに
- ［交換法則］任意の$m,n\in\Z$に対して$m+n=n+m$が成り立つ
を満たすので，群$(\Z,+)$は可換群である．
(1)-(3)の性質が成り立つ時点で群となり，可換群となるかどうかは(4)の性質が成り立つかどうかで決まるわけですね．
例２（可換群$(\R_+,\cdot)$）
正の実数全部の集合$\R_+$と通常の掛け算$\cdot$の組$(\R_+,\cdot)$が可換群であることを示せ．
３つの性質
- ［結合法則］任意の$x,y,z\in\R_+$に対して$(x\cdot y)\cdot z= x\cdot (y\cdot z)$が成り立つ
- ［単位元の存在］任意の$x\in\R_+$に対して$1\cdot x=x\cdot 1=x$が成り立つ
- ［逆元の存在］任意の$x\in\R_+$に対して$x\cdot x^{-1}=x^{-1}\cdot x=1$が成り立つ
を満たすから組$(\R_+,\cdot)$は群である（単位元は$1$で，$x\in\R_+$の逆元は$x^{-1}$）．さらに
- ［交換法則］任意の$x,y\in\R_+$に対して$x\cdot y=y\cdot x$が成り立つ
を満たすので，群$(\R_+,\cdot)$は可換群である．
あくまで「単位元は演算して相手を変えない元」という意識が大切です．
例１では演算が足し算だったので$0$が単位元でしたが，例２では演算が掛け算だったので$1$が単位元となります．
例３（群でない組$(\Z,\cdot)$）
整数全部の集合$\Z$と通常の掛け算$\cdot$の組$(\Z,\cdot)$が群でないことを示せ．
もし組$(\Z,\cdot)$が群であると仮定する．このとき，任意の$n\in\Z$に対して$1\cdot n=n\cdot1=n$が成り立つから$1$は単位元である．
しかし，$2\in\Z$に対して$2\cdot n=1$をみたすような$\Z$の元は存在しないから，$2\in\Z$は逆元を持たない
群は任意の元が逆元を持つから，仮定に矛盾するので組$(\Z,\cdot)$は群でない．
例１と例３で考えている集合は同じ$\Z$ですが，演算が異なると群になったりならなかったりします．
また，例２と例３では考えている演算は同じ$\cdot$ですが，集合が異なると群になったりならなかったりします．
このように，群は集合と演算の両方が決まって初めて考えられるということを意識しておきましょう．
例えば「自然数の集合$\Z$は群か？」と問われても，演算が何か分からないため群であるかどうか答えようがないので，「$\Z$に定義されている演算は何ですか？」と逆に問い返すことになります．
例４（非可換群$(\mrm{GL}_2(\R),\cdot)$）
３つの性質
- ［結合法則］任意の$A,B,C\in\mrm{GL}_2(\R)$に対して$(A\cdot B)\cdot C= A\cdot (B\cdot C)$が成り立つ
- ［単位元の存在］任意の$A\in\mrm{GL}_2(\R)$に対して$I_2\cdot A=A\cdot I_2=A$が成り立つ（$I_2$は２次単位行列）
- ［逆元の存在］任意の$A\in\mrm{GL}_2(\R)$に対して$A\cdot A^{-1}=A^{-1}\cdot A=I_2$が成り立つ
を満たすから組$(\mrm{GL}_2(\R),\cdot)$は群である（単位元は$I_2$で，$A\in\mrm{GL}_2(\R)$の逆元は$A^{-1}$）．ところが，
より［交換法則］を満たさないので，群$(\mrm{GL}_2(\R),\cdot)$は可換群ではない．
一般に実数成分の２次正則行列全部の集合$\mrm{GL}_2(\R)$と掛け算$\cdot$の組$(\mathrm{GL}_n(\R),\cdot)$も群となります．
この非可換群$(\mathrm{GL}_n(\R),\cdot)$は重要な非可換群のひとつで，一般線形群（general linear group）と呼ばれています．
単位元と逆元の一意性
最後に単位元と逆元の一意性を証明しておきましょう．
単位元の一意性
群$(G,\cdot)$の単位元$e$は一意である．
$V$の単位元$e,e’$を任意にとる．単位元を演算しても他の元を変えないから
なので，単位元はもとよりひとつしかない．
好きに２つとったにも関わらず同じものであることが示されたわけですから，元からひとつしかなかったという論法ですね．この論法は一意性を示す際によく用いられるので知っておくと良いでしょう．
この論法がしっくりこない方は，背理法で「異なる２つの単位元$e,e’$が存在すると仮定したが，$e=e’$が示されたので矛盾」と考えても構いません．
逆元の一意性
逆元の一意性も同じ論法で証明することができます．
群$(G,\cdot)$の任意の元$g$に対して，$g$の逆元はただひとつである．
$g\in G$の逆元$h,h’$を任意にとる．逆元を演算すると単位元になることと，結合法則より
なので，$g$の逆元はもとよりひとつしかない．
演算の記号$+$と$\cdot$の使い分け
演算の記号としては$+$と$\cdot$が用いられることが多いですが，使われ方や記法が少し異なるので注意しておきます．
加法の記号$+$
群の演算を$+$で表している場合，$+$は可換であると解釈するのが普通で，可換でない演算を$+$で表すのは適切ではありません．また，
- $+$で表される演算を加法
- $g+h$を$g$に$h$を加える
- $+$の演算の結果を和
と呼びます．
また，群$(\Z,+)$の$n$の逆元が$-n$であるように，加法$+$の逆元は前に「マイナス（$-$）」をつけて表すのが一般的です．
可換群$(G,+)$において，$g,h\in G$に対して$g$に$h$の逆元$-h$を加えたときの和は本来は$g+(-h)$ですが，これを$g-h$と表します．
乗法の記号$\cdot$
群の演算を$\cdot$で表している場合，$\cdot$は可換と非可換の両方がありえます．また，
- $\cdot$で表される演算を乗法
- $g\cdot h$を$g$に$h$をかける
- $\cdot$の演算の結果を積
と呼びます．
また，群$(\R_+,\cdot)$の$x$の逆元が$x^{-1}$であるように，乗法$\cdot$の逆元は右上に「マイナス１（$-1$）」をつけて表すのが一般的です．
さらに，多くの場合で$\cdot$を省略することも多く，群$(G,\cdot)$において，$g,h\in G$に対して$g$に$h$をかけたときの積は本来は$g\cdot h$ですが，これを$gh$と表します．
参考文献
以下は参考文献です．
代数学１ 群論入門
[雪江明彦 著/日本評論社]
本書は群論の入門書です．また，続巻として
- 第２巻「環と体とガロア理論」
- 第３巻「代数学のひろがり」
があります．
代数学は抽象的な分野と言われますが，抽象を理解するためには具体の理解が大切なことも多いです．
本書は具体例が多く扱われており，初学者にも読み進めやすい良著です．さらに，章末問題は基本問題から少し考える問題まで様々なレベルのものがあります．
また読むために必要な基礎事項を第１章にまとめてあり，予備知識をあまり仮定せずに独学で学びやすいのも嬉しい点です．
なお，本書については，以下の記事で書評としてまとめています．
【オススメの教科書｜代数学１ 群論入門(雪江明彦著，日本評論社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています．
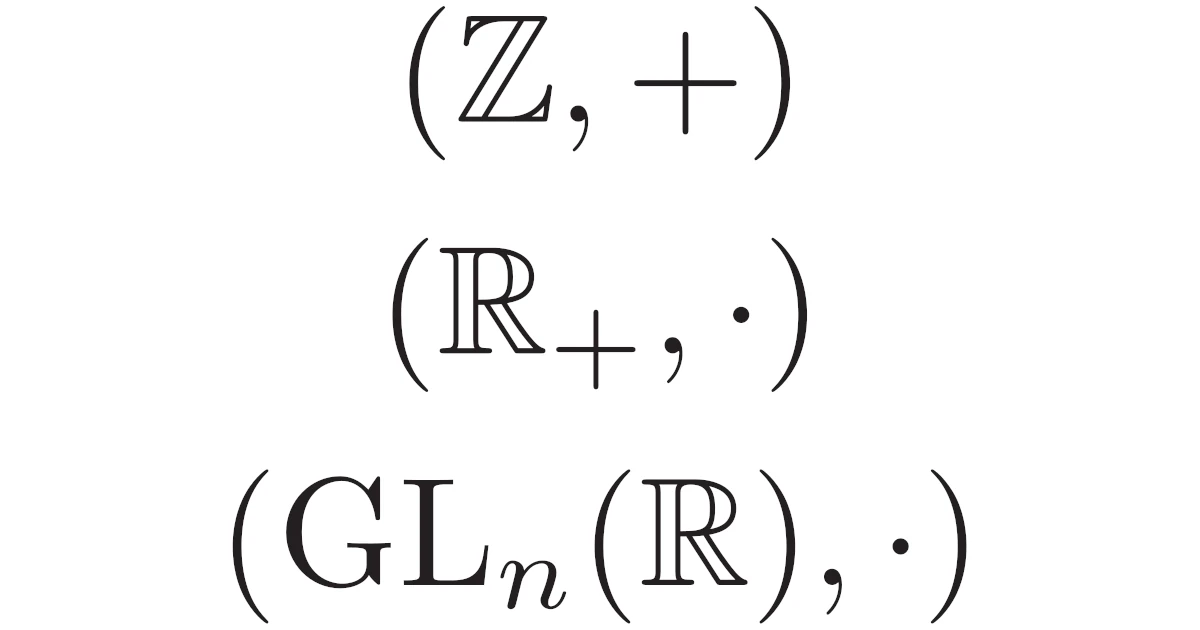
コメント