$x$の１次方程式$3x=2$は両辺に$3$の逆数$3^{-1}$をかけて$x=\dfrac{2}{3}$と解けますね．
これと同様のことを連立１次方程式でも考えてみましょう．例えば連立１次方程式$\begin{cases}x+2y=1\\3x+5y=7\end{cases}$は行列とベクトルの積により
\begin{align*}\bmat{1&2\\3&5}\bmat{x\\y}=\bmat{1\\7}\end{align*}
と表すことができるのでした．そこで，もし$\bmat{1&2\\3&5}$の「逆数」に相当する行列$\bmat{1&2\\3&5}^{-1}$があれば，これを両辺に左からかけて
\begin{align*}\bmat{x\\y}=\bmat{1&2\\3&5}^{-1}\bmat{1\\7}\end{align*}
と解$x,y$が求められそうな気がします．
実際いま考えたことはきちんと正当化することができ，この行列$\bmat{1&2\\3&5}^{-1}$を行列$\bmat{1&2\\3&5}$の逆行列といいます．
この記事では
- 逆行列の定義
- 逆行列を用いた連立方程式の解法
- 逆行列の具体例
を順に説明します．
なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
線形代数学の参考文献
以下は線形代数学に関するオススメの教科書です．
大学教養 線形代数（加藤文元 著）
数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．
手を動かしてまなぶ 線形代数（藤岡敦 著）
理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．
逆行列の定義
逆行列を定義するには正方行列と単位行列が必要なので確認しておきましょう．
正方行列と単位行列（復習）
$n\times n$行列を$n$次正方行列という．
要は列の数と行の数が等しい行列を正方行列というわけですね．例えば，
\begin{align*}\bmat{1&2\\3&4},\quad
\bmat{\sqrt{2}&-3\\\pi&e},\quad
\bmat{0&0\\0&0},\quad
\bmat{1&2&3\\4&5&6\\7&8&9}\end{align*}
は全て正方行列です．
$n$次正方行列$A$の第$(k,k)$成分 ($k=1,2,\dots,n$)を$A$の対角成分という．$A$の対角成分が全て$1$で，その他の成分が全て$0$であるとき，$A$を$n$次単位行列という．
単位行列は$I$や$E$で表すことが多く，次数を明示するときには$I_{n}$や$E_{n}$などと添字で表すことが多いです．例えば
\begin{align*}\bmat{1&0\\0&1},\quad
\bmat{1&0&0\\0&0&1\\0&0&1},\quad
\bmat{1&0&0&0\\0&0&1&0\\0&0&1&0\\0&0&0&1}\end{align*}
は全て単位行列で，それぞれ$I_2$, $I_3$, $I_4$などと表すわけですね．
単位行列の性質
単位行列は次の意味で実数の$1$に相当する行列であるということができます．
$I_{m}=(c_{ij})$とすると単位行列は対角成分が全て$1$でその他の成分は全て$0$だから，$c_{ik}=\begin{cases}1,&i=k,\\0,&i\neq k\end{cases}$である．
よって，$A=(a_{ij})$とすると行列の積の定義より$I_{m}A$の第$(i,j)$成分は
\begin{align*}\sum_{k=1}^{m}c_{ik}a_{kj}
=&c_{i1}a_{1j}+\dots+c_{ii}a_{ij}+\dots+c_{im}a_{mj}
\\=&0\cdot a_{1j}+\dots+1\cdot a_{ij}+\dots+0\cdot a_{mj}
=a_{ij}\end{align*}
である．これは$A$の第$(i,j)$成分だから，$I_{m}A=A$が成り立つ．
また，$AI_n=A$も同様に成り立つ．
つまり，単位行列を右からかけても左からかけても，相手の行列は変化しないわけですね．
例えば，$A=\bmat{1&2&3\\4&5&6}$として実際に計算してみると，確かに
\begin{align*}I_{2}A
=&\bmat{1&0\\0&1}\bmat{1&2&3\\4&5&6}
\\=&\bmat{1\cdot1+0\cdot4&2\cdot1+0\cdot5&3\cdot1+0\cdot6\\1\cdot0+1\cdot4&2\cdot0+1\cdot5&3\cdot0+1\cdot6}
\\=&\bmat{1&2&3\\4&5&6}
=A,
\\AI_{3}
=&\bmat{1&2&3\\4&5&6}\bmat{1&0&0\\0&1&0\\0&0&1}
\\=&\bmat{1\cdot1+2\cdot0+3\cdot0&1\cdot0+2\cdot1+3\cdot0&1\cdot0+2\cdot0+3\cdot1\\4\cdot1+5\cdot0+6\cdot0&4\cdot0+5\cdot1+6\cdot0&4\cdot0+5\cdot0+6\cdot1}
\\=&\bmat{1&2&3\\4&5&6}
=A\end{align*}
となりますね．
逆行列の定義
そもそも実数$a$の逆数$b$とは「$a\times b=b\times a=1$を満たす数」のことをいうのでした．
いま見たように積に関して単位行列$I$が実数の$1$に相当するのでしたから，次のように定義される逆行列が実数でいう逆数に相当することが分かりますね．
$n$次正方行列$A$が正則 (regular)であるとは
\begin{align*}AB=BA=I_n\end{align*}
をみたす$n$次正方行列$B$が存在することをいう．このとき，$B$は$A$の逆行列 (inverse matrix)であるといい，$B$を$A^{-1}$と表す．
例えば，
\begin{align*}\bmat{1&2\\3&5}\bmat{-5&2\\3&-1}=\bmat{1&2\\3&5}\bmat{-5&2\\3&-1}=\bmat{1&0\\6&1}\end{align*}
であることが実際に計算することで分かります．よって，$\bmat{1&2\\3&5}$は正則行列で
\begin{align*}\bmat{1&2\\3&5}^{-1}=\bmat{-5&2\\3&-1}\end{align*}
ということになるわけですね．
$\bmat{1&2\\3&5}^{-1}=\bmat{-5&2\\3&-1}$をどのように見つけるかについてはのちの記事で解説しています．
次のことも当たり前にしておきましょう．
正則行列$A$に対して，$A$の逆行列は１つしかない．
任意の$A$の逆行列$B$, $C$を考える．このとき
\begin{align*}B=IB=(CA)B=C(AB)=CI=C\end{align*}
となるから，$A$の逆行列は１つである．
逆行列を用いた連立１次方程式の解法
冒頭で説明したように次の問題を逆行列を用いて解いてみましょう．
$x,y$の連立１次方程式$\begin{cases}x+2y=1\\3x+5y=7\end{cases}$を解け．
この連立１次方程式は
\begin{align*}\bmat{1&2\\3&5}\bmat{x\\y}=\bmat{1\\7}\end{align*}
と表すことができる．上の例で$\bmat{1&2\\3&5}^{-1}=\bmat{5&2\\3&1}$であることをみたから，両辺に左から$\bmat{-5&2\\3&-1}$をかけて
\begin{align*}\bmat{x\\y}=\bmat{-5&2\\3&-1}\bmat{1\\7}=\bmat{9\\-4}\end{align*}
となって，解$(x,y)=(9,-4)$を得る．
正則行列の性質
実数の場合には$0$でなければ逆数を持ちますが，行列の場合には零行列$O$でなくても逆行列を持たないことがあります．
正則行列の列と行
正則行列はどの行，どの列も零ベクトルでない．
背理法により示す．正則行列$A=[\m{a}_{1},\dots,\m{a}_{n}]$の第$k$列$\m{a}_{k}$が$\m{0}$であると仮定し，$A$の逆行列を$B$とすると
\begin{align*}I=&BA=[B\m{a}_{1},\dots,B\m{a}_{n}]
\\=&[B\m{a}_{1},\dots,B\m{a}_{k-1},\m{0},B\m{a}_{k+1},\dots,B\m{a}_{n}]\end{align*}
であるが，$I$の第$k$行は零ベクトルでないから矛盾である．よって，仮定は誤りで$A$のどの列も零ベクトルでない．
行に関しては，$A$を行ベクトルで表して積$AB$を考えれば，同様に従う．
例えば，$\bmat{1&1\\0&0}$は零行列$O$ではありませんが，今の命題から逆行列を持たないわけですね．
正則行列の積
正則行列の行列の積も正則行列です．
正則な$n$次正方行列$A$, $B$に対して，積$AB$は正則であり，$(AB)^{-1}=B^{-1}A^{-1}$が成り立つ．
$AA^{-1}=A^{-1}A=BB^{-1}=B^{-1}B=I$より
\begin{align*}&(AB)(B^{-1}A^{-1})=A(BB^{-1})A^{-1}=AIA^{-1}=AA^{-1}=I,
\\&(B^{-1}A^{-1})(AB)=B^{-1}(A^{-1}A)B=B^{-1}IB=B^{-1}B=I\end{align*}
が成り立つから，$(AB)^{-1}=B^{-1}A^{-1}$を得る．
$AB$と$B^{-1}A^{-1}$をかけると，$A$, $B$が打ち消しあって単位行列となってくれるわけですね．
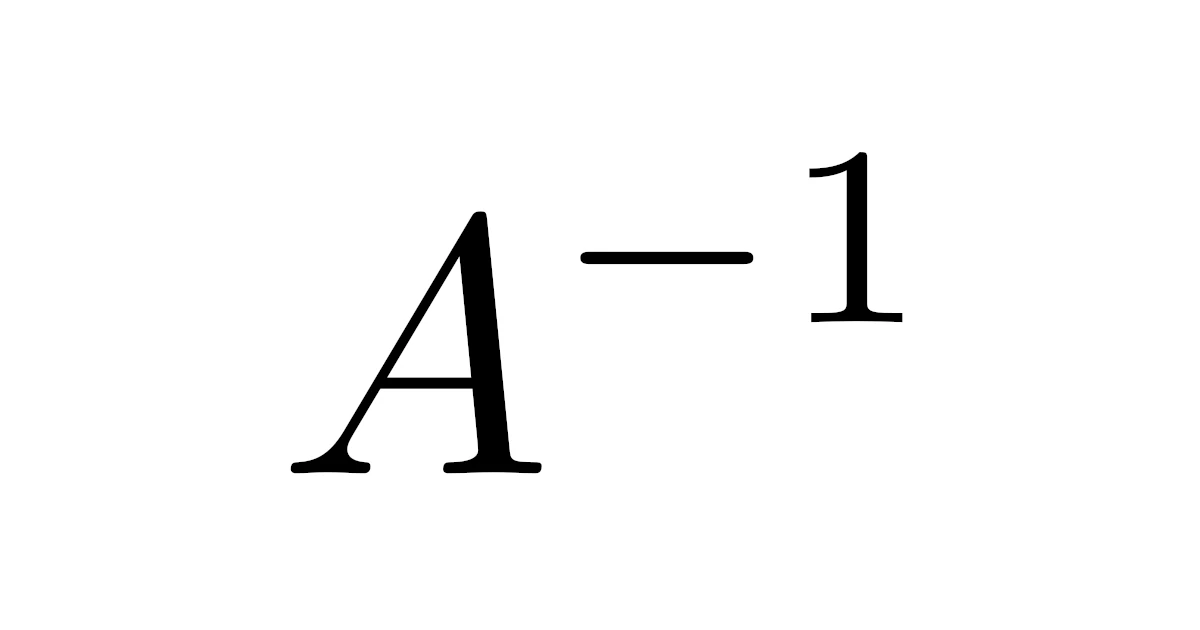
コメント