複素積分の定義と例題｜複素平面上での積分の考え方と計算方法

複素解析は「複素数を与えると複素数を返す関数」である複素関数が主役となる分野なのでした．

微分積分学で学ぶリーマン積分は実変数$x$を区間$[a,b]$で動かして考える積分$\dint_{a}^{b}f(x)\,dx$でしたが，複素解析で学ぶ複素積分は複素変数$z$を複素平面上の曲線$C$上で動かして考える積分$\dint_{C}f(z)\,dz$となります．

また，実はリーマン積分と複素積分の定義は形式的に同じなので，リーマン積分の定義を理解していれば複素積分の定義も同様に理解することができます．

この記事では

リーマン積分と複素積分
複素積分の具体例
複素積分の基本性質

を順に説明します．

「複素解析の基本」の一連の記事

リーマン積分と複素積分

最初にリーマン積分がどのような考え方の積分だったかを確認し，そのあとに複素積分を定義します．

リーマン積分の復習

微分積分学で学ぶ基本の積分はリーマン積分で，長方形で面積を近似する考え方の積分なのでした．

下図のような区間$[a,b]$上の有界関数$f$に対して，面積水色領域の面積をリーマン積分の考え方で考えてみましょう．

区間$[a,b]$を

$\begin{align*}x_{0}<x_{1}<x_{2}<\dots<x_{n}\quad(a=x_{0},b=x_{n})\end{align*}$

と分割し，全ての小区間$[x_{i-1},x_{i}]$上に代表点$\xi_{i}$をとります($i=1,\dots,n$)．

このときの各小区間$[x_{i-1},x_{i}]$でできる長方形の面積を足し合わせたものは

$\begin{align*}\sum_{i=1}^{n}f(\xi_{i})(x_{i}-x_{i-1})\quad\dots(*)\end{align*}$

となりますね．この$(*)$は目標としている最初の水色部分の面積の近似になっており，この和をリーマン和というのでした．

この状態ではあくまで近似でしかありませんが，小区間$[x_{i-1},x_{i}]$の幅$x_{i}-x_{i-1}$が全て０に近付くように極限をとると，誤差はどんどん小さくなり最初の水色部分の面積に収束しそうに思えます．

そこで，代表点$\xi_{i}$の取り方によらず$(*)$が同じ値に近付くなら，$[a,b]$上で$f$はリーマン可積分であるといい，その値を

$\begin{align*}\int_{a}^{b}f(x)\,dx\end{align*}$

と表し，これを$[a,b]$上の$f$のリーマン積分というのでした．

ここで$f$が連続関数であれば，いつでもリーマン積分可能であることを思い出しておきましょう．

［連続関数のリーマン積分］関数$f$が$[a,b]$上の連続なら，$[a,b]$上で$f$はリーマン可積分である．

複素積分の定義

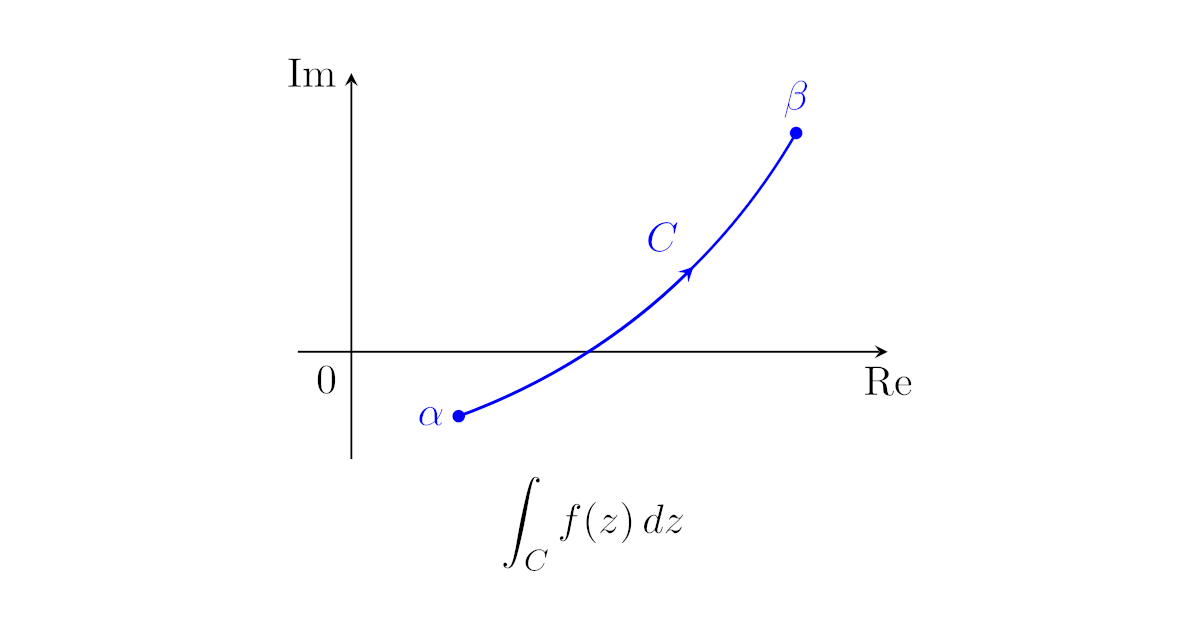
リーマン積分は数直線上の区間$[a,b]$上で変数$x$を動かして考える積分でしたが，複素積分は複素平面上の曲線$C$上で変数$z$を動かして考える積分です．

やっていることはリーマン積分の定義と形式的には全く同じです．

［複素積分］複素平面上の有限の長さをもつ曲線$C$と$C$上で連続な複素関数$f$を考える．$C$は向き付きとし，$C$の始点を$\alpha$，終点を$\beta$とする．さらに，曲線$C$を

$\begin{align*}z_{0},z_{1},z_{2},\dots,z_{n}\quad(\alpha=z_{0},\beta=z_{n})\end{align*}$

で順に分割する．

さらに，曲線$C$上の$z_{i-1}$から$z_{i}$の間（端点含む）の点$\xi_{i}$をとる($i=1,\dots,n$)．

このとき，和

$\begin{align*}\sum_{i=1}^{n}f(\xi_{i})(z_{i}-z_{i-1})\quad\dots(*)\end{align*}$

で$z_{i}-z_{i-1}$が全て０に近づくように極限をとったとき，$\xi_i$の取り方によらず和$(*)$は一定の値に近付き，この値を積分経路$C$上の$f$の複素積分または複素線積分といい，

$\begin{align*}\int_{C}f(z)\,dz\end{align*}$

と表す．

先ほど紹介したように連続関数のリーマン積分は必ず存在するのでした．複素積分でも$f$が$C$上で連続関数であることから，和$(*)$の極限は必ず収束します．

リーマン積分と複素積分では「区間$[a,b]$」が「始点$\alpha$から終点$\beta$までの曲線$C$」に変わっているだけで，和が

$\begin{align*}\sum_{i=1}^{n}f(\xi_{i})(x_{i}-x_{i-1}) \quad\leftrightarrow\quad \sum_{i=1}^{n}f(\xi_{i})(z_{i}-z_{i-1})\end{align*}$

と対応しているのが見てとれますね．

よって，複素積分の積分経路$C$を実軸上の区間$[a,b]$とすると，

$\begin{align*}\int_{C}f(z)\,dz=\int_{a}^{b}f(x)\,dx\end{align*}$

となりますね．つまり，複素積分は実軸から複素平面上へ拡張した積分になっているわけですね．

複素積分の具体例

それでは具体的に複素積分を計算してみましょう．

例１（${}1$の複素積分）

複素平面上の有限の長さをもつ曲線$C$の始点と終点をそれぞれ$\alpha$, $\beta$とする．このとき，複素積分

$\begin{align*}\int_{C}\,dz\end{align*}$

を求めよ．

実数の場合と同じく$\dint_{C}\,dz$は$\dint_{C}1\,dz$の省略です．

定義に従って計算しましょう．

$f(z)=1$とし，曲線$C$を点

$\begin{align*}z_{0},z_{1},z_{2},\dots,z_{n}\quad(\alpha=z_{0},\beta=z_{n})\end{align*}$

で順に分割する．

和$\dsum_{i=1}^{n}f(z_{i})(z_{i}-z_{i-1})$は多くの項が打ち消し合い

$\begin{align*}\sum_{i=1}^{n}f(z_{i})(z_{i}-z_{i-1}) =\sum_{i=1}^{n}1\cdot(z_{i}-z_{i-1}) =z_n-z_0=\beta-\alpha\end{align*}$

となるから，複素積分の定義より$z_{i}-z_{i-1}$が全て０に近づくように極限をとると

$\begin{align*}\int_{C}\,dz=\beta-\alpha\end{align*}$

である．

例２（$z$の複素積分）

複素平面上の有限の長さをもつ曲線$C$の始点と終点をそれぞれ$\alpha$, $\beta$とする．このとき，複素積分

$\begin{align*}\int_{C}z\,dz\end{align*}$

を求めよ．

少し工夫が必要ですが，この例２も定義に従って計算しましょう．

複素積分の各区間の代表点$\xi_i$として$\xi_i=z_i$や$\xi_i=z_{i-1}$ととっても収束することに注意してください．

$g(z)=z$とし，曲線$C$を点

$\begin{align*}z_{0},z_{1},z_{2},\dots,z_{n}\quad(\alpha=z_{0},\beta=z_{n})\end{align*}$

で順に分割する．

複素積分の定義より，$z_{i}-z_{i-1}$が全て０に近づくように極限をとると

$\begin{align*}&I:=\sum_{i=1}^{n}g(z_{i})(z_{i}-z_{i-1})=\sum_{i=1}^{n}z_{i}(z_{i}-z_{i-1}), \\&I\!I:=\sum_{i=1}^{n}g(z_{i-1})(z_{i}-z_{i-1})=\sum_{i=1}^{n}z_{i-1}(z_{i}-z_{i-1})\end{align*}$

はどちらも$\dint_{C}z\,dz$に収束する．また，多くの項が打ち消し合い

$\begin{align*}I+I\!I&=\{({z_1}^2-z_1z_0)+({z_2}^2-z_2z_1)+\dots+({z_n}^2-z_nz_{n-1})\} \\&+\{(z_0z_1-{z_0}^2)+(z_1z_2-{z_1}^2)+\dots+(z_{n-1}z_n-{z_{n-1}}^2)\} \\&={z_n}^2-{z_0}^2=\beta^2-\alpha^2\end{align*}$

となるから，$z_{i}-z_{i-1}$が全て$0$に近づくように極限をとると

$\begin{align*}&2\int_{C}z\,dz=\beta^2-\alpha^2 \\&\iff\int_{C}z\,dz=\frac{1}{2}(\beta^2-\alpha^2)\end{align*}$

である．

例３（複素積分をリーマン積分に帰着させる方法）

上の２つの例では積分経路は始点と終点以外が自由でしたが，多くの複素積分は具体的な積分経路で考えます．

$n$を$-1$でない整数とし，$R>0$とする．複素平面上の曲線$C$を原点中心，半径$R$の円周とする．このとき，複素積分

$\begin{align*}\int_{C}z^{n}\,dz,\quad \int_{C}\frac{1}{z}\,dz\end{align*}$

を求めよ．ただし，積分経路$C$の向きは反時計回りとする．

積分経路が具体的に与えられている場合には$z\in C$を実数に変数変換してリーマン積分に帰着させることができます．

$C$は原点中心・半径$R$の円周なので，$z\in C$は$z=R(\cos{t}+i\sin{t})$（$0\le t\le2\pi$）と極形式で表せますね．

両辺を$t$で微分して

$\begin{align*}\od{z}{t}=R(\sin{t}-i\cos{t})\end{align*}$

であることと併せて，$z$を$t$に置換して計算することができます．

複素積分がリーマン積分と同様に定義されているので，複素積分でも置換積分できることはリーマン積分と同様に証明できます．

$z\in C$は$z=R(\cos{t}+i\sin{t})$（$0\le t\le2\pi$）と表せる．$\od{z}{t}=R(-\sin{t}+i\cos{t})$なので

$\begin{align*}\int_{C}z^{n}\,dz &=\int_{0}^{2\pi}R^{n}(\cos{nt}+i\sin{nt})\cdot R(-\sin{t}+i\cos{t})\,dt \\&=R^{n+1}\int_{0}^{2\pi}\{(-\sin{nt}\cos{t}-\cos{nt}\sin{t}) \\&\hspace{3cm}+i(\cos{nt}\cos{t}-\sin{nt}\sin{t})\}\,dt \\&=R^{n+1}\int_{0}^{2\pi}\{-\sin{(n+1)t}+i\cos{(n+1)t}\}\,dt=0\end{align*}$

であり，

$\begin{align*}\int_{C}\frac{1}{z}\,dz &=\int_{C}\frac{\overline{z}}{|z|^{2}}\,dz =\frac{1}{R^{2}}\int_{C}\overline{z}\,dz \\&=\frac{1}{R^{2}}\int_{0}^{2\pi}R(\cos{t}-i\sin{t})\cdot R(-\sin{t}+i\cos{t})\,dt \\&=\int_{0}^{2\pi}i(\cos^{2}{t}+\sin^{2}{t})\,dt =\int_{0}^{2\pi}i\,dt=2\pi i\end{align*}$