線形部分空間の定義｜証明のテンプレートも例題に沿って紹介

例えば，実数係数の多項式全部の集合

$\begin{align*}\R[x]=\set{a_0+a_1x+\dots+a_nx^n}{\begin{aligned}&a_0,a_1,\dots,a_n\in\R;\\&n=0,1,2,\dots\end{aligned}}\end{align*}$

は通常の和とスカラー倍により線形空間となります．また，実数係数の２次以下の多項式全部の集合

$\begin{align*}\R[x]_2=\set{a_0+a_1x+a_2x^2}{a_0,a_1,a_2\in\R}\end{align*}$

も通常の和とスカラー倍により線形空間となります．

いま $R [x]_{2}$ は $R [x]$ の部分集合であり， $R [x]$ と同じ和・スカラー倍により線形空間となっており，このことを $R [x]_{2}$ は $R [x]$ の線形部分空間であるといいます．

この記事では

線形部分空間の定義
線形部分空間であることの証明の例題
線形部分空間の基本性質

を順に解説します．

列ベクトルの線形空間 $R^{n}$ の線形結合だけで十分なら，列ベクトルの部分空間に絞って解説した以下の記事の方が分かりやすいでしょう．

数ベクトル空間の部分空間の定義｜証明のテンプレも例題から解説

ℝⁿの和とスカラー倍について閉じている部分集合をℝⁿの「部分空間」と言い，直感的には原点を通り真っ直ぐに伸びた空間ということができます．この記事では部分空間を具体例とともに説明しています．

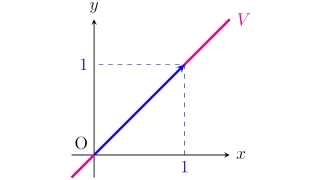
「線形空間の基本」の一連の記事

線形空間
1. 1 線形空間はℝⁿの一般化！定義と具体例を解説
2. 2 部分空間の定義と証明のテンプレを例題から解説 (今の記事)
3. 3 線形結合・線形独立性の考え方を具体例から解説
4. 4 ベクトルたちが生成（span）する線形部分空間
5. 5 線形空間の基底の定義と証明のテンプレートを紹介
6. 和空間・共通部分の定義と考え方を例題から解説(準備中)

線形写像
1. 線形写像は行列の一般化！定義と具体例を解説(準備中)
2. 線形写像は基底が命！基底との重要な関係(準備中)
3. 線形写像の像Im(f)とKer(f)の定義と例題(準備中)
4. 線形空間の同型の定義と次元定理を解説(準備中)
5. 線形空間が同型と次元の超重要な関係(準備中)

スクロールできます

線形部分空間の定義
線形部分空間であることの証明の例題
線形部分空間の基本性質
1. 和・スカラー倍が閉じていることの言い換え
2. 線形部分空間が線形空間であること

線形部分空間の定義

まずは線形部分空間を定義します．

体 $F$ 上の線形空間 $V$ と空でない $U \subset V$ を考える．任意の $u, v \in U$ , $k \in F$ に対して

$\begin{align*}\m{u}+\m{v},k\m{u}\in U\end{align*}$

を満たすとき， $U$ を $V$ の線形部分空間（linear subspace）または単に部分空間（subspace）という．

もとの $V$ は線形空間なので部分集合 $U$ の元の和もスカラー倍も $V$ には必ず属していますが，下手な $U$ を考えると $U$ の元の和やスカラー倍が $U$ の外に出てしまうことがあります．

一方， $U$ が和とスカラー倍が閉じているときには，のちに示すように $U$ は $V$ と同じ和とスカラー倍について線形空間になることが証明でき，線形部分空間と呼ぶわけですね．

また，定義の条件について

任意の $u, v \in U$ に対して $u + v \in U$ が成り立つことを， $U$ は $V$ の和について閉じている
任意の $u \in U$ , $k \in F$ に対して $k u \in U$ が成り立つことを， $U$ は $V$ のスカラー倍について閉じている

といいます．

のちに示すように，(2)の条件はもう少し便利に書き換えることもできます．

スクロールできます

線形部分空間であることの証明の例題

線形部分空間であることの証明では

空集合でない
和について閉じている
スカラー倍について閉じている

を示すのがテンプレートです．

例１（多項式の線形部分空間）

冒頭で挙げた多項式の線形空間 $R [x]$ の線形部分空間の例をきちんと証明しておきましょう．

実数係数の多項式全部の線形空間 $R [x]$ に対して，その２次以下のものを全部集めてできる部分集合

$\begin{align*}\R[x]_2:=\set{a_0+a_1x+a_2x^2\in\R[x]}{a_0,a_1,a_2\in\R}\end{align*}$

は $R [x]$ の線形部分空間となることを示せ．

零多項式 $0$ は２次以下の実数係数多項式なので $0 \in R [x]_{2}$ である．

よって， $R [x]_{2} \neq \emptyset$ だから，あとは $R [x]_{2}$ が $R [x]$ の和とスカラー倍について閉じていることを示せば良い．

和について閉じていることの証明

任意の $f (x), g (x) \in R [x]_{2}$ をとり， $f (x) = a_{0} + a_{1} x + a_{2} x^{2}$ , $g (x) = b_{0} + b_{1} x + b_{2} x^{2}$ とおく（ $a_{0}, a_{1}, a_{2}, b_{0}, b_{1}, b_{2} \in R$ ）．

和 $f (x) + g (x)$ について

$\begin{align*}f(x)+g(x)=(a_0+b_0)+(a_1+b_1)x+(a_2+b_2)x^2\end{align*}$

となっており， $a_{0} + b_{0}, a_{1} + b_{1}, a_{2} + b_{2} \in R$ と併せて， $f (x) + g (x) \in R [x]_{2}$ が成り立つ．よって， $R [x]_{2}$ は和について閉じている．

スカラー倍について閉じていることの証明

任意の $f (x) \in R [x]_{2}$ , $k \in R$ をとり， $f (x) = a_{0} + a_{1} x + a_{2} x^{2}$ とおく（ $a_{0}, a_{1}, a_{2} \in R$ ）．

スカラー倍 $k f (x)$ について

$\begin{align*}kf(x)=(ka_0)+(ka_1)x+(ka_2)x^2\end{align*}$

となっており， $k a_{0}, k a_{1}, k a_{2} \in R$ と併せて， $k f (x) \in R [x]_{2}$ が成り立つ．よって， $R [x]_{2}$ はスカラー倍について閉じている．

具体的には， $R [x]_{2}$ の和が閉じているというのは

$\begin{align*}(3+x-2x^2)+(1+x^2)=4+x-x^2\end{align*}$

も $R [x]_{2}$ に属しているということで，スカラー倍が閉じているというのは

$\begin{align*}2(3+x-2x^2)=6+2x-4x^2\end{align*}$

も $R [x]_{2}$ に属しているということですね．

上の解答では，このように $R [x]_{2}$ でのあらゆる和とスカラー倍が $R [x]_{2}$ に属していることを示したわけですね．

一般に $n$ 次以下の多項式全部の部分集合 $R [x]_{n}$ も $R [x]$ の線形部分空間となります．

例２（ $R^{n}$ の線形部分空間）

基本的な線形空間である実数成分の $n$ 次列ベクトル全部の空間 $R^{n}$ の線形部分空間を考えましょう．

$R^{3}$ の部分集合

$\begin{align*}U=\set{\bmat{x\\y\\z}\in\R^3}{\begin{gathered}x+y+z=0,\\x-z=0\end{gathered}}\end{align*}$

が $R^{3}$ の線形部分空間となることを示せ．

$U$ は

(第１成分)+(第２成分)+(第３成分)=0
(第１成分)-(第３成分)=0

を満たす $R^{3}$ の部分集合で，図形的には $x y z$ 空間上の平面 $x + y + z = 0$ と平面 $x - z = 0$ の交線ですね．

$0 + 0 + 0 = 0$ , $0 - 0 = 0$ なので $[\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}] \in U$ である．

よって， $U \neq \emptyset$ だから，あとは $U$ が $R^{3}$ の和とスカラー倍について閉じていることを示せば良い．

和について閉じていることの証明

任意に $a, b \in U$ をとり， $a = [\begin{matrix} x \\ y \\ z \end{matrix}]$ , $b = [\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix}]$ とおく（ $x, y, z, x^{'}, y^{'}, z^{'} \in R$ ）．このとき， $U$ の定義から

$\begin{align*}&x+y+z=0,\quad x-z=0, \\&x'+y'+z'=0,\quad x'-z'=0\end{align*}$

を満たす．和 $a + b = [\begin{matrix} x + x^{'} \\ y + y^{'} \\ z + z^{'} \end{matrix}]$ について

$\begin{align*}&(x+x')+(y+y')+(z+z')\\&=(x+y+z)+(x'+y'+z')=0, \\&(x+x')-(z+z')=(x-z)+(x'-z')=0\end{align*}$

となっており， $x + x^{'}, y + y^{'}, z + z^{'} \in R$ と併せて， $a + b \in U$ が成り立つ．よって， $U$ は和について閉じている．

スカラー倍について閉じていることの証明

任意に $a \in U$ , $k \in R$ をとり， $a = [\begin{matrix} x \\ y \\ z \end{matrix}]$ とおく（ $x, y, z \in R$ ）．このとき， $U$ の定義から

$\begin{align*}x+y+z=0,\quad x-z=0\end{align*}$

を満たす．スカラー倍 $k a = [\begin{matrix} k x \\ k y \\ k z \end{matrix}]$ について

$\begin{align*}&(kx)+(ky)+(kz)=k(x+y+z)=0, \\&(kx)-(kz)=k(x-z)=0\end{align*}$

となっており， $k x, k y, k z \in R$ と併せて， $k a \in U$ が成り立つ．よって， $U$ はスカラー倍について閉じている．

例３（数列の線形部分空間）

実数列の線形空間 $ℓ (R)$ の漸化式を満たす部分集合が線形部分空間となる例もよく扱われます．

実数列全部の線形空間 $ℓ (R)$ の部分集合

$\begin{align*}U=\set{\{a_n\}\in\ell(\R)}{a_{n+2}+a_{n+1}+a_{n}=0}\end{align*}$

が $ℓ (R)$ の線形部分空間となることを示せ．

$U$ は漸化式 $a_{n + 2} + a_{n + 1} + a_{n} = 0$ をみたす実数列 ${a_{n}}$ 全部の部分集合ですね．

$0 + 0 + 0 = 0$ なので $(0, 0, 0, \dots) \in U$ である．

よって， $U \neq \emptyset$ だから，あとは $U$ が $ℓ (R)$ の和とスカラー倍について閉じていることを示せば良い．

和について閉じていることの証明

任意に ${a_{n}}, {b_{n}} \in U$ をとる．このとき， $U$ の定義から

$\begin{align*}&a_{n+2}+a_{n+1}+a_{n}=0,\quad b_{n+2}+b_{n+1}+b_{n}=0\end{align*}$

を満たす．和 ${a_{n}} + {b_{n}} = {a_{n} + b_{n}}$ について

$\begin{align*}&(a_{n+2}+b_{n+2})+(a_{n+1}+b_{n+1})+(a_{n}+b_{n}) \\&=(a_{n+2}+a_{n+1}+a_{n})+(b_{n+2}+b_{n+1}+b_{n}) \\&=0+0=0\end{align*}$

となっており， $a_{n} + b_{n} \in R$ と併せて， ${a_{n}} + {b_{n}} \in U$ が成り立つ．よって， $U$ は和について閉じている．

スカラー倍について閉じていることの証明

任意に ${a_{n}} \in U$ , $k \in R$ をとる．このとき， $U$ の定義から

$\begin{align*}a_{n+2}+a_{n+1}+a_{n}=0\end{align*}$

を満たす．スカラー倍 $k {a_{n}} = {k a_{n}}$ について

$\begin{align*}&(ka_{n+2})+(ka_{n+1})+(ka_{n}) \\&=k(a_{n+2}+a_{n+1}+a_{n}) =k\cdot0=0\end{align*}$

となっており， $k a_{n} \in R$ と併せて， $k {a_{n}} \in U$ が成り立つ．よって， $U$ はスカラー倍について閉じている．

線形部分空間の基本性質

ここでは２つの性質を証明します．

和・スカラー倍が閉じていることの言い換え

線形空間 $V$ と $U \subset V$ に対して，次は互いに同値である．

任意の $u, v \in U$ , $k \in F$ に対して $u + v, k u \in U$ が成り立つ．
任意の $u, v \in U$ , $k, ℓ \in F$ に対して $k u + ℓ v \in U$ が成り立つ．
任意の $u, v \in U$ , $k \in F$ に対して $k u + v \in U$ が成り立つ．

この命題の(1)は $U$ が $V$ の線形部分空間であることの必要十分条件でしたから，この命題の(2)または(3)を示しても $U$ が $V$ の線形部分空間が示されることになりますね．

(1)では和とスカラー倍が閉じていることを別々に証明することになりますが，(2), (3)はひとつの式を証明すればよいので(1)よりも手軽です．

$(1) ⟹ (2)$ の証明

任意に $u, v \in U$ , $k, ℓ \in F$ をとる．(1)が成り立つなら， $U$ はスカラー倍について閉じているから $k u, ℓ v \in U$ であり，さらに和について閉じているから

$\begin{align*}k\m{u}+\ell\m{v}\in U\end{align*}$

が成り立つ．よって，(2)が従う．

$(2) ⟹ (3)$ の証明

任意に $u, v \in U$ , $k \in F$ をとる．(2)が成り立つなら，

$\begin{align*}k\m{u}+\m{v}=k\m{u}+1\m{v}\in U\end{align*}$

が成り立つ．よって，(3)が従う．

$(3) ⟹ (1)$ の証明

任意に $u, v \in U$ , $k \in F$ をとる．(3)が成り立つなら，

$\begin{align*}&\m{u}+\m{v}=1\m{u}+\m{v}\in U, \\&k\m{u}=k\m{u}+\m{0}\in U\end{align*}$

が成り立つ．よって，(1)が従う．

この証明では例えば $(3) ⟹ (2)$ が証明されていないように見えるかもしれません．しかし， $(3) ⟹ (1)$ と $(1) ⟹ (2)$ が証明されているので，(1)を経由することで $(3) ⟹ (2)$ が成り立つことが分かりますね．

他の $(1) ⟹ (3)$ と $(2) ⟹ (1)$ も同様に成り立つことが分かります．

線形部分空間が線形空間であること

線形空間 $V$ の線形部分空間 $U$ は $V$ と同じ和とスカラー倍により線形空間となる．

$V$ は線形空間だから，線形空間の定義より次の８性質を満たす．

［１］和について

任意の $u, v, w \in V$ に対し， $(u + v) + w = u + (v + w)$
任意の $u \in V$ に対し， $0 + u = u + 0 = u$ （ $0$ は $V$ の零ベクトル）
任意の $u \in V$ に対し， $u + (- u) = 0$
任意の $u, v \in V$ に対し， $u + v = v + u$

［２］スカラー倍について

任意の $u \in V$ , $k, ℓ \in F$ に対し， $(k ℓ) \cdot u = k \cdot (ℓ \cdot u)$
任意の $u \in V$ に対し， $1 \cdot u = u$

［３］和とスカラー倍について

任意の $u, v \in V$ , $k \in F$ に対し， $k \cdot (u + v) = k \cdot u + k \cdot v$
任意の $u \in V$ , $k, ℓ \in F$ に対し $(k + ℓ) \cdot u = k \cdot u + ℓ \cdot u$

$U$ は $V$ の部分集合だから， $V$ の任意の元に対して成り立つ(1), (4)-(8)は $U$ においても成り立つ．

また， $U$ は線形部分空間だから空でなく， $U$ はスカラー倍について閉じているから，任意の $u \in U$ に対して

$\begin{align*}\m{0}=0\m{u}\in U,\quad -\m{u}=(-1)\m{u}\in U\end{align*}$

が成り立つ．よって，(2), (3)も $U$ において成り立つ．

線形部分空間の定義

線形部分空間であることの証明の例題

例１（多項式の線形部分空間）

和について閉じていることの証明

スカラー倍について閉じていることの証明

例２（Rnの線形部分空間）

和について閉じていることの証明

スカラー倍について閉じていることの証明

例３（数列の線形部分空間）

和について閉じていることの証明

スカラー倍について閉じていることの証明

線形部分空間の基本性質

和・スカラー倍が閉じていることの言い換え

(1)⟹(2)の証明

(2)⟹(3)の証明

(3)⟹(1)の証明

線形部分空間が線形空間であること

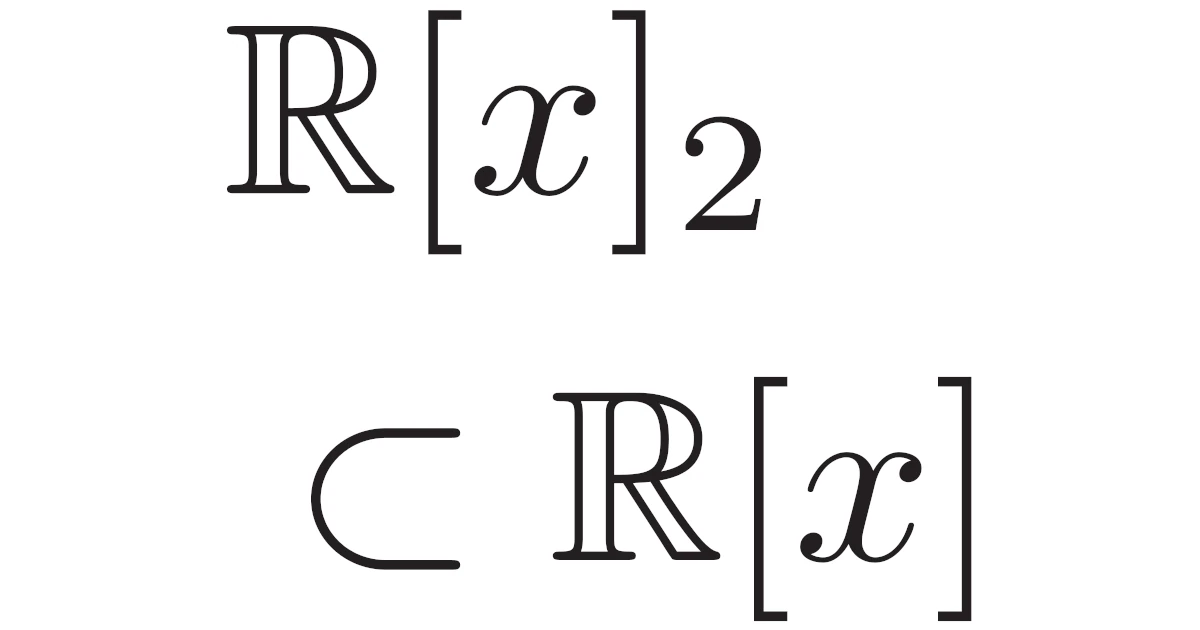
コメント

例２（ $R^{n}$ の線形部分空間）

$(1) ⟹ (2)$ の証明

$(2) ⟹ (3)$ の証明

$(3) ⟹ (1)$ の証明