実数列$\{a_n\}$に対して極限$\lim\limits_{n\to\infty}a_n$を考えることはよくありますが，実数列はいつでも収束するとは限らないのでした．
そこで，極限の一歩手前のものとして上極限$\limsup\limits_{n\to\infty}a_n$と下極限$\liminf\limits_{n\to\infty}a_n$を考えることがよくあり，普通の極限とは違って上極限と下極限は（$\pm\infty$を許せば）いつでも存在するという良さがあります．
上極限と下極限の定義は一見ややこしそうに見えますが，具体例を考えるとイメージを掴みやすいです．
また，上極限と下極限が一致することと，通常の極限が存在することが同値というのも，上極限と下極限の重要な性質です．
この記事では
- 上極限と下極限の考え方
- 上極限と下極限の定義と具体例
- 上極限$\limsup$と下極限$\liminf$の性質
- 参考文献
を順に解説します．
上極限と下極限の考え方
まずは一般項が$a_n=\dfrac{1}{n}$の実数列$\{a_n\}$を考えましょう．この数列$\{a_n\}$を初項から順に書き並べると
\begin{align*}1,\ \frac{1}{2},\ \frac{1}{3},\ \frac{1}{4},\ \frac{1}{5},\dots\end{align*}
となっていますね．
上極限の考え方
この実数列$\{a_n\}$に対して，
- 集合$\{a_1,a_2,a_3,\dots\}$
- 集合$\{a_2,a_3,a_4,\dots\}$
- 集合$\{a_3,a_4,a_5,\dots\}$
の上限$\sup$を考えましょう．それぞれ
\begin{align*}\sup\{a_1,a_2,a_3,\dots\}=&\sup\brb{1,\frac{1}{2},\frac{1}{3},\dots}=1,
\\\sup\{a_2,a_3,a_4,\dots\}=&\sup\brb{\frac{1}{2},\frac{1}{3},\frac{1}{4},\dots}=\frac{1}{2},
\\\sup\{a_3,a_4,a_5,\dots\}=&\sup\brb{\frac{1}{3},\frac{1}{4},\frac{1}{5},\dots}=\frac{1}{3}\end{align*}
ですね．このように$\{a_n,a_{n+1},a_{n+2},\dots\}$の上限$\sup$を追いかけていくと，
\begin{align*}\lim_{n\to\infty}\sup\{a_n,a_{n+1},a_{n+2},\dots\}=\lim_{n\to\infty}\frac{1}{n}=0\end{align*}
となります．このように，$a_1$から項を少なくしていったときの$\sup\{a_n,a_{n+1},a_{n+2},\dots\}$の近付き先を実数列$\{a_n\}$の上極限といいます．
下極限の考え方
下極限は上極限の下限バージョンです．つまり，この実数列$\{a_n\}$に対して，
- 集合$\{a_1,a_2,a_3,\dots\}$
- 集合$\{a_2,a_3,a_4,\dots\}$
- 集合$\{a_3,a_4,a_5,\dots\}$
の下限$\inf$はそれぞれ
\begin{align*}\sup\{a_1,a_2,a_3,\dots\}=&\sup\brb{1,\frac{1}{2},\frac{1}{3},\dots}=0,
\\\sup\{a_2,a_3,a_4,\dots\}=&\sup\brb{\frac{1}{2},\frac{1}{3},\frac{1}{4},\dots}=0,
\\\sup\{a_3,a_4,a_5,\dots\}=&\sup\brb{\frac{1}{3},\frac{1}{4},\frac{1}{5},\dots}=0\end{align*}
ですね．このように$\{a_n,a_{n+1},a_{n+2},\dots\}$の下限$\inf$を追いかけていくと，
\begin{align*}\lim_{n\to\infty}\inf\{a_n,a_{n+1},a_{n+2},\dots\}=&\lim_{n\to\infty}0=0\end{align*}
となります．このように，$a_1$から項を少なくしていったときの$\inf\{a_n,a_{n+1},a_{n+2},\dots\}$の近付き先を実数列$\{a_n\}$の下極限といいます．
上極限と下極限の定義と具体例
いまの上極限，下極限を一般の場合にきちんと定義して，具体例を考えましょう．
上極限$\varlimsup\limits_{n\to\infty}a_n$と下極限$\varliminf\limits_{n\to\infty}a_n$の定義
実数列$\{a_n\}$に対して，
\begin{align*}\lim\limits_{n\to\infty}\Bigl(\sup_{p\ge n}a_p\Bigr),\quad
\lim\limits_{n\to\infty}\Bigl(\inf_{p\ge n}a_p\Bigr)\end{align*}
をそれぞれ実数列$\{a_n\}$の上極限，下極限といい，$\varlimsup\limits_{n\to\infty}a_n$, $\varliminf\limits_{n\to\infty}a_n$と表す．
上極限を$\limsup\limits_{n\to\infty}a_n$，下極限を$\liminf\limits_{n\to\infty}a_n$と表すこともある．
つまり，
- $a_1$以降の上限，$a_2$以降の上限，……と続けていったときの近付き先が上極限$\varlimsup\limits_{n\to\infty}a_n$
- $a_1$以降の下限，$a_2$以降の下限，……と続けていったときの近付き先が下極限$\varliminf\limits_{n\to\infty}a_n$
というわけですね．
いくつか具体例を考えましょう．
具体例１（$a_n=(-1)^n$）
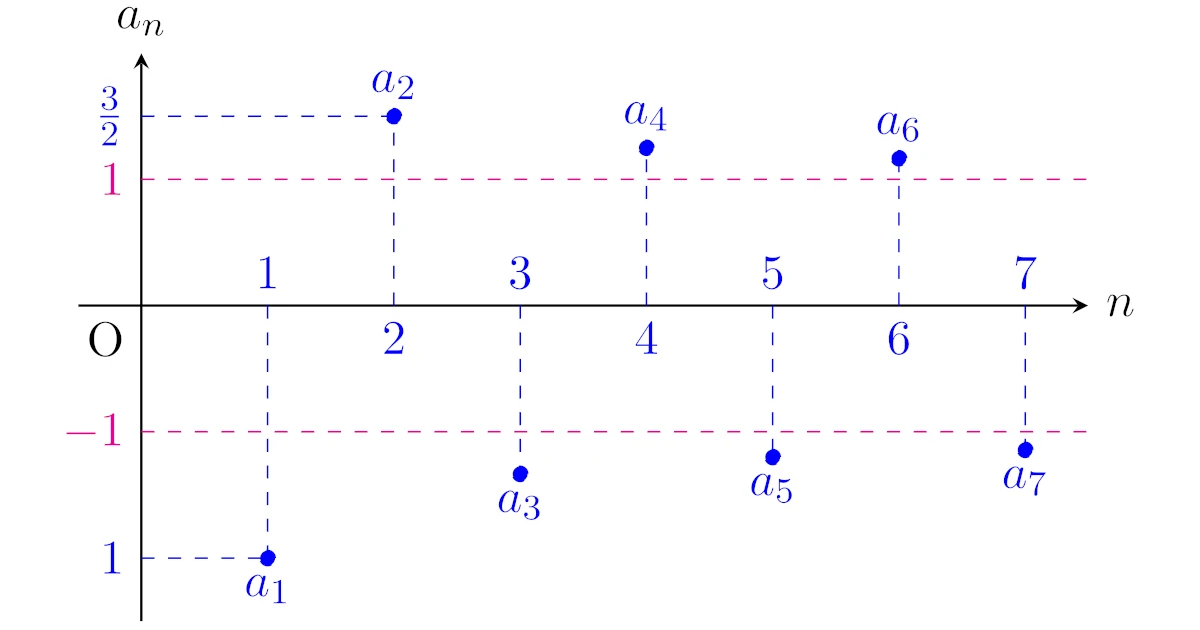
一般項が$a_n=(-1)^n$の数列$\{a_n\}$の上極限と下極限を求めよ．
数列$\{a_n\}$を初項から順に書き並べると
\begin{align*}-1,\ 1,\ -1,\ 1,\ -1,\dots\end{align*}
である．
上極限$\varlimsup\limits_{n\to\infty}a_n$を求める
$\sup_{p\ge 1}a_p$を順に考えると，
\begin{align*}1=\sup_{p\ge 1}a_p=\sup_{p\ge 2}a_p=\sup_{p\ge 3}a_p=\dots\end{align*}
となり$\sup\limits_{p\ge n}a_p=1$だから，$\varlimsup\limits_{n\to\infty}a_n=1$である．
下極限$\varliminf\limits_{n\to\infty}a_n$を求める
$\inf_{p\ge 1}a_p$を順に考えると，
\begin{align*}-1=\inf_{p\ge 1}a_p=\inf_{p\ge 2}a_p=\inf_{p\ge 3}a_p=\dots\end{align*}
となり$\inf\limits_{p\ge n}a_p=-1$だから，$\varliminf\limits_{n\to\infty}a_n=-1$である．
普通の極限$\lim\limits_{n\to\infty}a_n$は存在しませんが，上極限と下極限は存在していますね．
冒頭でも書いたように，実数列の上極限と下極限は（$\pm\infty$を許せば）必ず存在します（のちに示します）．
具体例１（$a_n=(-1)^n(1+\frac{1}{n})$）
一般項が
\begin{align*}a_n=(-1)^n\bra{1+\frac{1}{n}}\end{align*}
の数列$\{a_n\}$の上極限と下極限を求めよ．
数列$\{a_n\}$を初項から順に書き並べると
\begin{align*}-2,\ \frac{3}{2},\ -\frac{4}{3},\ \frac{5}{4},\ -\frac{6}{5},\ \frac{7}{6},\ -\frac{8}{7},\ \dots\end{align*}
である．
上極限$\varlimsup\limits_{n\to\infty}a_n$を求める
$\sup_{p\ge 1}a_p$を順に考えると，
\begin{align*}&\sup_{p\ge 1}a_p=\sup_{p\ge 2}a_p=\frac{3}{2},
\\&\sup_{p\ge 3}a_p=\sup_{p\ge 4}a_p=\frac{5}{4},
\\&\sup_{p\ge 5}a_p=\sup_{p\ge 6}a_p=\frac{7}{6},\dots\end{align*}
となり，$\varlimsup\limits_{n\to\infty}a_n=1$である．
下極限$\varliminf\limits_{n\to\infty}a_n$を求める
$\inf_{p\ge 1}a_p$を順に考えると，
\begin{align*}&\inf_{p\ge 1}a_p=-2,
\\&\inf_{p\ge 2}a_p=\inf_{p\ge 3}a_p=-\frac{4}{3}
\\&\inf_{p\ge 4}a_p=\inf_{p\ge 5}a_p=-\frac{6}{5},\dots\end{align*}
となり，$\varliminf\limits_{n\to\infty}a_n=-1$である．
上極限$\limsup$と下極限$\liminf$の性質
それでは，上極限と下極限の性質を説明します．
以下，見やすくするため$\sup\limits_{p\ge n}a_p$を$\overline{a_n}$で表し，$\inf\limits_{p\ge n}a_p$を$\underline{a_n}$で表しましょう．このとき，上極限は$\lim\limits_{n\to\infty}\overline{a_n}$と下極限は$\lim\limits_{n\to\infty}\underline{a_n}$と表せますね．
上極限と下極限の存在
任意の実数列$\{a_n\}$に対して，上極限と下極限は（$\pm\infty$を許せば）常に存在する．
便宜上，$\pm\infty$も実数のように扱うと
- $\{\overline{a_n}\}$は広義単調減少な数列
- $\{\underline{a_n}\}$は広義単調増加な数列
である．一般に広義単調な数列は（$\pm\infty$を許して）極限をもつから，$\lim\limits_{n\to\infty}\overline{a_n}$, $\lim\limits_{n\to\infty}\underline{a_n}$が存在する．
すなわち，上極限と下極限が存在する．
$\pm\infty$を実数に加えた集合$\R\cup\{\pm\infty\}$を拡大実数といいます．拡大実数上では$\pm\infty$も実数のように扱うことができ，上記の証明も正当化できます．
定数で評価されている数列の上極限と下極限の不等式
普通の極限と同様に次が成り立ちます．
［命題１］実数列$\{a_n\}$と$c\in\R$について，次が成り立つ．
- ある$N\in\N$が存在して，$n>N$で$c\ge a_n$なら$c\ge\varlimsup\limits_{n\to\infty}a_n$が成り立つ．
- ある$N\in\N$が存在して，$n>N$で$c\le a_n$なら$c\le\varliminf\limits_{n\to\infty}a_n$が成り立つ．
$n>N$とする．$c\ge a_n$の両辺で上限$\sup\limits_{p\ge n}$をとって，極限$n\to\infty$をとると
\begin{align*}c\ge\lim_{n\to\infty}\overline{a_n}=\varlimsup_{n\to\infty}a_n\end{align*}
を得る．
同様に$c\le a_n$の両辺で下限$\inf\limits_{p\ge n}$をとって，極限$n\to\infty$をとると$c\le\varliminf\limits_{n\to\infty}a_n$が得られる．
上極限と下極限について，次は基本的な不等式です．
［命題２］実数列$\{a_n\}$に対して，$\varlimsup\limits_{n\to\infty}a_n\ge\varliminf\limits_{n\to\infty}a_n$が成り立つ．
一般に実数の集合$S$に対して$\sup S\ge \inf S$が成り立つから，任意の$n\in\N$に対して
\begin{align*}&\sup\{a_n,a_{n+1},\dots\}\ge\inf\{a_n,a_{n+1},\dots\}\iff\overline{a_n}\ge\underline{a_n}\end{align*}
が成り立つ．よって，両辺で極限$n\to\infty$をとれば
\begin{align*}\varlimsup\limits_{n\to\infty}a_n\ge\varliminf\limits_{n\to\infty}a_n\end{align*}
が得られる．
上極限と下極限が一致することと極限が存在することは同値
上極限と下極限を用いて，極限が存在するための必要十分条件を述べることができます．
実数列$\{a_n\}$に対して，次は同値である．
- 上極限$\varlimsup\limits_{n\to\infty}a_n$と下極限$\varliminf\limits_{n\to\infty}a_n$がともに収束して一致する
- 極限$\lim\limits_{n\to\infty}a_n$が存在する
上極限$\varlimsup\limits_{n\to\infty}a_n$と下極限$\varliminf\limits_{n\to\infty}a_n$がともに収束して一致するとき，不等式
\begin{align*}\underline{a_n}\le a_n\le\overline{a_n}\end{align*}
で極限$n\to\infty$をとると，はさみうちの原理から極限$\lim\limits_{n\to\infty}a_n$が存在する．
逆に極限$\lim\limits_{n\to\infty}a_n$が存在するとする．$\alpha:=\lim\limits_{n\to\infty}a_n$とし，任意に$\epsilon>0$をとる．
このとき，ある$N\in\N$が存在して，
\begin{align*}n>N\Ra \alpha-\epsilon<a_n<\alpha+\epsilon\end{align*}
が成り立つ．よって，先ほどの［命題１］から
\begin{align*}\varliminf\limits_{n\to\infty}a_n\ge\alpha-\epsilon,\quad
\varlimsup_{n\to\infty}a_n\le\alpha+\epsilon\end{align*}
が成り立つから
\begin{align*}\varlimsup\limits_{n\to\infty}a_n-\varliminf\limits_{n\to\infty}a_n\le2\epsilon\end{align*}
を得る．
また，先ほどの［命題２］より$0\le\varlimsup\limits_{n\to\infty}a_n-\varliminf\limits_{n\to\infty}a_n$であることを併せると，$\epsilon$の任意性より$\varlimsup\limits_{n\to\infty}a_n=\varliminf\limits_{n\to\infty}a_n$が成り立つ．
この証明から，さらに次が成り立つことまで言えますね．
実数列$\{a_n\}$と$\alpha\in\R$に対して，次は同値である．
- $\varlimsup\limits_{n\to\infty}a_n=\varliminf\limits_{n\to\infty}a_n=\alpha$
- $\lim\limits_{n\to\infty}a_n=\alpha$
参考文献
解析入門
[杉浦光男 著/東京大学出版会]
解析学の教科書としては非常に有名で，理論系で解析がしっかり必要となる人は持っておいてよいテキストです．
- 第１巻で１変数の微分積分学
- 第２巻で多変数の微分積分学
を扱っています．本書に対応した演習書「解析演習」も出版されています．
本書の特徴としては
- 数学的に厳密に書かれている
- 基本的な微分積分学の知識体系は網羅されている
の２点が挙げられます．
このため，辞書的に使う教科書という位置付けて持っている人も多いようです．
なお，この記事の内容は第１巻に載っています．
微分積分学
[笠原晧司 著/サイエンス社]
微分積分学の教科書として有名な名著です．
具体例を多く扱いイメージを掴むことに重点を置きつつ，議論もきっちりしているため，大学１年生の微分積分学をしっかり学びたい人には心強い味方になると思います．
具体例のレベルは基本的なものに加えて少々難しいものも含まれているので，いろいろな具体例に触れたい人は持っておいてもよいでしょう．
このため，しっかり数学をやりたい人の微分積分学の導入としてオススメできる一冊です．
コメント