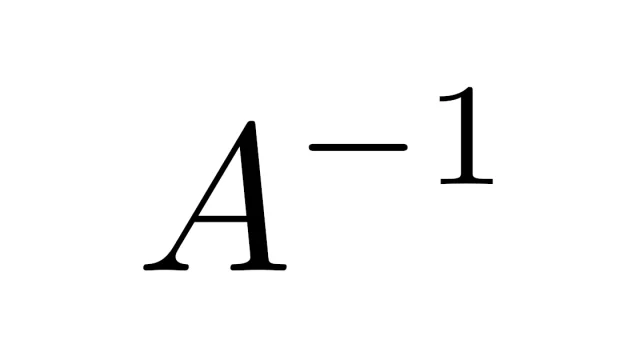 線形代数学の基本
線形代数学の基本 正則行列の定義・具体例|逆行列を使った連立1次方程式の解法
0でない実数には逆数がありますが,行列にて対してこの逆数に相当するものを逆行列といいます.逆行列は線形代数でとても大切なもので,この記事では具体例を考えながら逆行列の定義と性質を丁寧に解説しています.
 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本 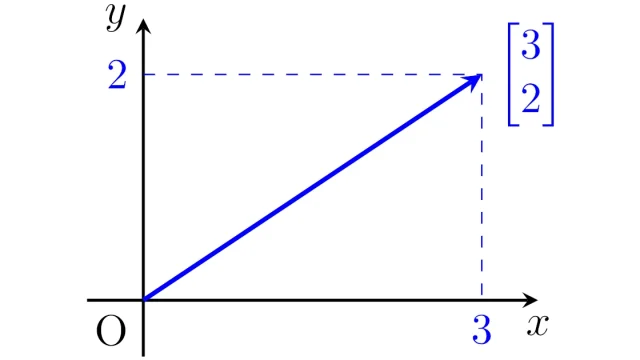 線形代数学の基本
線形代数学の基本 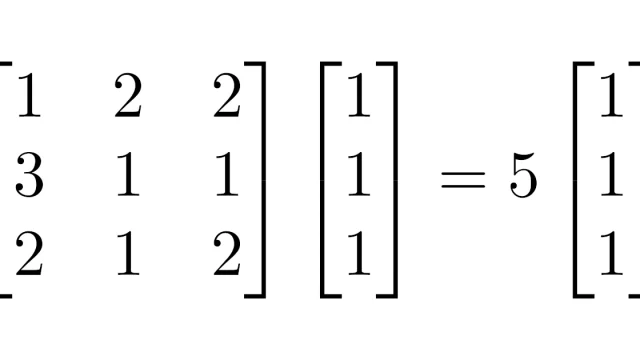 線形代数学
線形代数学  線形代数学
線形代数学