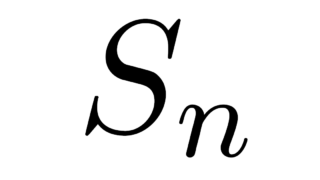 線形代数学の基本
線形代数学の基本 行列式のために置換を定義する|代数学でも重要な置換の基礎
正方行列Aの行列式|A|が0かどうかで,Aの正則性を判定することができます.行列式|A|を定義するには置換を用いる方法が一般的です.この記事では,行列式を定義するための置換の定義と性質を説明します.
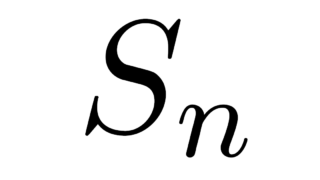 線形代数学の基本
線形代数学の基本 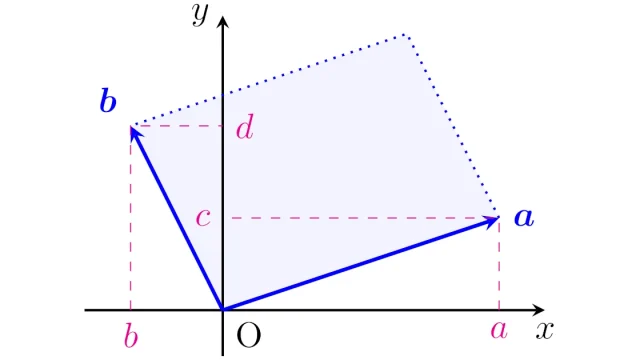 線形代数学の基本
線形代数学の基本 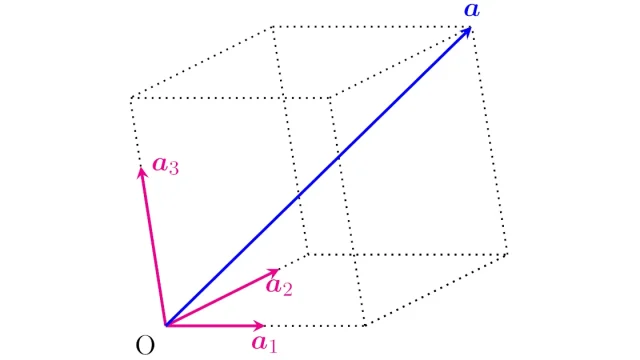 線形代数学の基本
線形代数学の基本 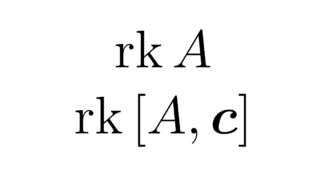 線形代数学の基本
線形代数学の基本 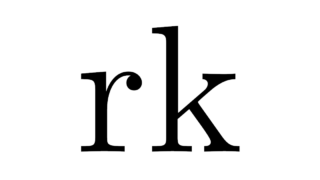 線形代数学の基本
線形代数学の基本 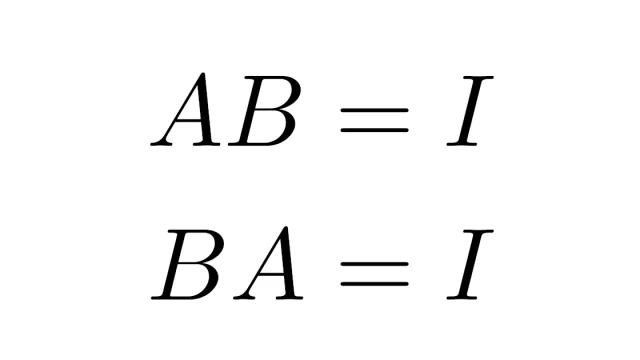 線形代数学の基本
線形代数学の基本 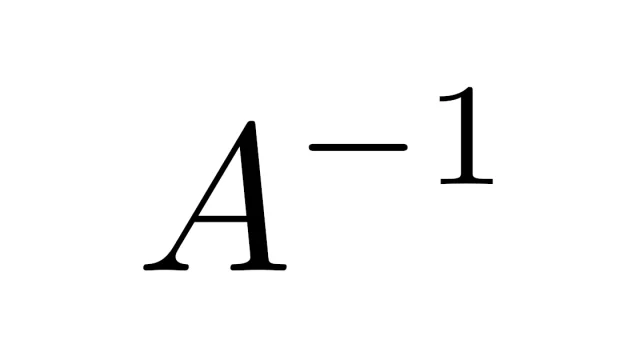 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本