２次列ベクトル全部の集合$\R^2$上の和とスカラー倍はそれぞれ
と定義され，交換法則や分配法則などの「よい性質」を満たします．
$\R^2$以外の集合上でも「よい性質」をもつ和とスカラー倍を考えると$\R^2$と同様に扱えることも多く，そのような空間を一般に線形空間といいます．
この記事では
- 線形空間の定義
- 線形空間の具体例
- 零ベクトルと逆ベクトルの一意性
を順に解説します．
「線形空間の基本」の一連の記事
- 線形空間
- 1 線形空間はℝⁿの一般化！定義と具体例を解説 (今の記事)
- 2 部分空間の定義と証明のテンプレを例題から解説
- 3 線形結合・線形独立性の考え方を具体例から解説
- 生成される部分空間と基底・次元の定義・求め方(準備中)
- 和空間・共通部分の定義と考え方を例題から解説(準備中)
- 線形写像
- 線形写像は行列の一般化！定義と具体例を解説(準備中)
- 線形写像は基底が命！基底との重要な関係(準備中)
- 線形写像の像Im(f)とKer(f)の定義と例題(準備中)
- 線形空間の同型の定義と次元定理を解説(準備中)
- 線形空間が同型と次元の超重要な関係(準備中)
線形空間の定義
最初に２次列ベクトル全部の空間$\R^2$の和とスカラー倍についての性質を確認し，それを踏まえて線形空間を定義します．
$\R^2$の和とスカラー倍の性質
［１］和について
- 任意の$\m{a},\m{b},\m{c}\in\R^n$に対し$(\m{a}+\m{b})+\m{c}=\m{a}+(\m{b}+\m{c})$
- 零ベクトル$\m{0}\in\R^n$は，任意の$\m{a}\in\R^n$に対し$\m{0}+\m{a}=\m{a}+\m{0}=\m{a}$
- 任意の$\m{a}\in\R^n$に対し$\m{a}+(-1)\m{a}=\m{0}$
- 任意の$\m{a},\m{b}\in\R^n$に対し$\m{a}+\m{b}=\m{b}+\m{a}$
［２］スカラー倍について
- 任意の$\m{a}\in\R^n$, $k,\ell\in\R$に対し$(k\ell)\m{a}=k(\ell\m{a})$
- 任意の$\m{a}\in\R^n$に対し$1\m{a}=\m{a}$
［３］和とスカラー倍について
- 任意の$\m{a},\m{b}\in\R^n$, $k\in\R$に対し$k(\m{a}+\m{b})=k\m{a}+k\m{b}$
- 任意の$\m{a}\in\R^n$, $k,\ell\in\R$に対し$(k+\ell)\m{a}=k\m{a}+\ell\m{a}$
ここで
- 和$+$は$\R^2$の２つのベクトル$\m{a}$, $\m{b}$を与えて，$\R^2$の１つのベクトル$\m{a}+\m{b}$を返す規則
- スカラー倍$\cdot$は$\R$の１つの元$k$と$\R^2$の１つのベクトル$\m{a}$を与えて，$\R^2$の１つのベクトル$k\m{a}$を返す規則
と言えることに注目しておきましょう．
線形空間の定義
いまみた$\R^2$の８性質を満たすような空間は，$\R^2$と同じような性質をもちそうに思えます．
そこで，この８性質に対応する性質を満たす空間$V$を線形空間といいます．
最初は以下の定義を見てもピンときにくいと思うので，深く考えず読み流して次の具体例に進んでしまっても良いでしょう．
体$\mathbb{F}$と空でない集合$V$に対して
- $V$の元を２つ与えて$V$の元を１つ返す$+$
- $\mathbb{F}$, $V$の元を１つずつ与えて$V$の元１つ返す$\cdot$
が定まっており，次の８性質を満たすとする．
［１］$+$について
- 任意の$\m{u},\m{v},\m{w}\in V$に対し$(\m{u}+\m{v})+\m{w}=\m{u}+(\m{v}+\m{w})$
- ある$\m{0}\in V$が存在して，任意の$\m{u}\in V$に対し$\m{0}+\m{u}=\m{u}+\m{0}=\m{u}$
- 任意の$\m{u}\in V$に対し，ある$\m{v}\in V$が存在し$\m{u}+\m{v}=\m{0}$
- 任意の$\m{u},\m{v}\in V$に対し$\m{u}+\m{v}=\m{v}+\m{u}$
［２］$\cdot$について
- 任意の$\m{u}\in V$, $k,\ell\in\mathbb{F}$に対し$(k\ell)\cdot\m{u}=k\cdot(\ell\cdot\m{u})$
- 任意の$\m{u}\in V$に対し$1\cdot\m{u}=\m{u}$
［３］$+$と$\cdot$について
- 任意の$\m{u},\m{v}\in V$, $k\in\mathbb{F}$に対し$k\cdot(\m{u}+\m{v})=k\cdot\m{u}+k\cdot\m{v}$
- 任意の$\m{u}\in V$, $k,\ell\in\mathbb{F}$に対し$(k+\ell)\cdot\m{u}=k\cdot\m{u}+\ell\cdot\m{u}$
このとき，$V$を$\mathbb{F}$上の線形空間（linear space）またはベクトル空間（vector space）といい，
- $+$を$V$上の和
- $\cdot$を$V$上のスカラー倍（または$\mathbb{F}$倍）
という．また，$V$の元をベクトル（vector）という．
さらに，性質(2)の$\m{0}$を$V$上の零ベクトル（zero vector）といい，性質(3)の$\m{v}$を$\m{u}$の逆ベクトル（inverse vector）という．$\m{u}$の逆ベクトルは$-\m{u}$と表し，和$\m{w}+(-\m{u})$を$\m{w}-\m{u}$と表す．
具体例のあとで零ベクトル$\m{0}$がひとつしか存在しないこと，任意のベクトルに対して逆ベクトルがひとつしか存在しないことを証明します．
スカラー倍の記号$\cdot$は$\R^2$の場合と同じく省略することが多いです．
実線形空間と複素線形空間
体$\mathbb{F}$としては
- 実数体$\R$
- 複素数体$\C$
のどちらかで考えることが多く，このときの線形空間を次のように呼びます．
実数体$\R$上の線形空間$V$を実線形空間といい，複素数体$\R$上の線形空間$V$を複素線形空間という．
スカラーが実数・複素数の線形空間をそれぞれ実線形空間・複素線形空間と呼ぶわけですね．
線形空間の具体例
具体例として
- 列ベクトルの線形空間$\R^n$
- 列ベクトルの線形空間$\C^n$
- 多項式の線形空間$\R[x]$
- 数列の線形空間$\ell(\R)$
を考えましょう．
例１（列ベクトルの線形空間$\R^n$）
２次列ベクトル全部の集合$\R^2$上で
- 通常の和$\bmat{a_1\\a_2}+\bmat{b_1\\b_2}=\bmat{a_1+b_1\\a_2+b_2}$
- 通常の$\R$倍$k\bmat{a_1\\a_2}=\bmat{ka_1\\ka_2}$
を考えると，この和と$\R$倍は線形空間の８性質を満たすので$\R^2$は実線形空間となります．
線形空間の元をベクトルと呼ぶのでしたから，例えば
などは全て$\R^2$のベクトルですね．
一般に$\R^n$に通常の和と通常の$\R$倍を定めると，$\R^2$と同様に$\R^n$は実線形空間となります．
例２（列ベクトルの線形空間$\C^n$）
２次列ベクトル全部の集合$\C^2$上で
- 通常の和$\bmat{a_1\\a_2}+\bmat{b_1\\b_2}=\bmat{a_1+b_1\\a_2+b_2}$
- 通常の$\C$倍$k\bmat{a_1\\a_2}=\bmat{ka_1\\ka_2}$
を考えると，この和と$\C$倍は線形空間の８性質を満たすので$\C^2$は複素線形空間となります．
線形空間の元をベクトルと呼ぶのでしたから，例えば
などは全て$\C^2$のベクトルですね．
一般に$\C^n$に通常の和と通常の$\C$倍を定めると，$\C^2$と同様に$\C^n$は実線形空間となります．
例３（多項式の線形空間$\R[x]$）
実数係数多項式全部の集合$\R[x]$上で
- 通常の和
- 通常の$\R$倍
を考えると，この和と$\R$倍は線形空間の８性質を満たすので$\R[x]$は実線形空間となります（次数が異なる多項式の和は次数の大きい方に合わせて考えます）．
線形空間の元をベクトルと呼ぶのでしたから，例えば
などは全て$\R[x]$のベクトルですね．
高校数学までは向きと大きさをもつものをベクトルと呼んで「矢印」で表していましたが，一般の線形空間のベクトルはまったく「矢印」のようでなくても構いません．ただ線形空間の元をベクトルと呼ぶだけです．
同様の和と$\C$倍を考えると，複素数係数多項式全部の集合$\C[x]$は複素線形空間となります．
例４（数列の線形空間$\ell(\R)$）
実数列全部の集合$\ell(\R)$上で
- 和$\{a_n\}+\{b_n\}=\{a_n+b_n\}$
- $\R$倍$k\{a_n\}=\{ka_n\}$
を考えると，この和と$\R$倍は線形空間の８性質を満たすので$\ell(\R)$は実線形空間となります．
$\ell(\R)$に属するひとつひとつの元が数列です．
例えば，
- 一般項が$a_n=n$の数列$\{a_n\}=(1,2,3,4,\dots)$
- 一般項が$b_n=(-1)^n$の数列$\{b_n\}=(-1,1,-1,1,\dots)$
に対して，和$\{a_n\}+\{b_n\}$は
であり，スカラー倍$3\{a_n\}$は
というわけです．つまり，一般項の和・スカラー倍を考えて新しい数列を作るわけですね．
線形空間の元をベクトルと呼ぶのでしたから，例えば
などは全て$\ell(\R)$のベクトルですね．
例３の繰り返しになりますが，一般の線形空間の元をベクトルと呼ぶだけで，ベクトルはまったく矢印のようでなくても構いません．
同様の和と$\C$倍を考えると，複素数列全部の集合$\ell(\C)$は複素線形空間となります．
零ベクトルと逆ベクトルの一意性
$\R^2$では零ベクトルが$\bmat{0\\0}$だけであることは成分の計算を考えれば分かりますが，線形空間は必ずしも$\R^2$のように分かりやすいものとは限りません．
しかし，どんな線形空間であっても零ベクトルと逆ベクトルの一意性が成り立つことを最後に証明しておきましょう．
零ベクトルの一意性
線形空間$V$の零ベクトル$\m{0}$はただひとつであり，任意の$\m{v}\in V$に対して$0\m{v}=\m{0}$である．
$V$の零ベクトル$\m{0},\m{0}’$を任意にとる．零ベクトルは足しても他の元を変えないから
が成り立つ．よって，零ベクトルはもとよりひとつしかない．
また，分配法則より
である．両辺に$0\m{v}$の逆元$-0\m{v}$を加えて$0\m{v}=\m{0}$を得る．
一意性の証明については，好きに２つとったにも関わらず同じものであることが示されたわけですから，元からひとつしかなかったという論法ですね．この論法は一意性を示す際によく用いられるので知っておくと良いでしょう．
この論法がしっくりこない方は，背理法で「異なる２つの零ベクトル$\m{0},\m{0}’$が存在すると仮定したが，$\m{0}=\m{0}’$が示されたので矛盾」と考えても構いません．
逆ベクトルの一意性
逆ベクトルの一意性も同じ論法で証明することができます．
線形空間$V$の任意の元$\m{v}$に対して，$\m{v}$の逆ベクトルはただひとつであり，$-\m{v}=(-1)\m{v}$である．
$\m{v}\in V$の逆ベクトル$\m{u},\m{u}’$を任意にとる．逆ベクトルを足すと零ベクトルになることと，結合法則より
なので，$\m{v}$の逆ベクトルはもとよりひとつしかない．
また，分配法則より
だから，逆ベクトルの定義より$-\m{v}=(-1)\m{v}$を得る．
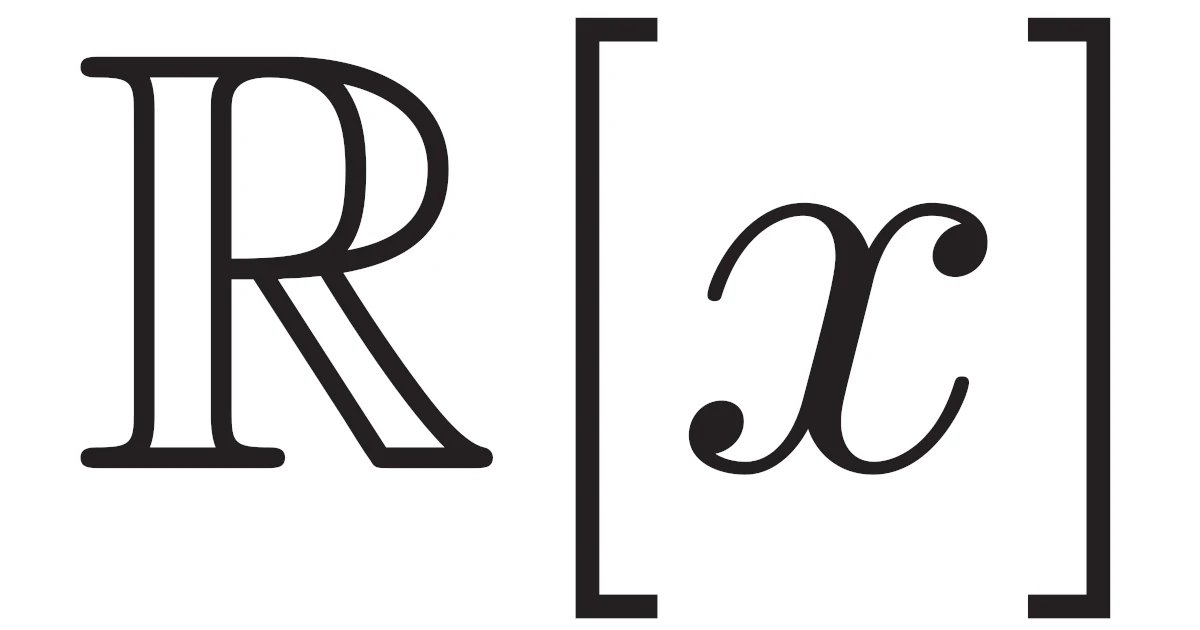
コメント