関数を表す際には
- 高校数学のテキストでは「関数$f(x)$」という表現が
- 大学数学のテキストでは「関数$f$」という表現が
多く用いられています.
これらの違いに大きな意味はないように思えるかもしれませんが,実はこれら“$f$”と“$f(x)$”の意味には大きな違いがあり,厳密には「関数$f$」の方が正しい言い方です.
とはいえ,必ずしも「関数$f(x)$」の言い方が悪いかというとそうではありません.
この記事では,これらの言い方の違いを説明します.
“$f(x)$”と“$f$”の違い
例えば“$f(2)$”が「$f$に$2$を与えて返ってくる『値』」のことであるように,“f(x)”はあくまで「値」でしかありません.
一方で値を与えて値を返す$f$こそが「関数」であり,この意味で“$f$”と“$f(x)$”は同じものではありません.
例えば,「関数$x^2+1$」という表現は「関数$f(x)$」型の言い方なので厳密には誤りで,これを厳密にいうなら
「$f(x)=x^2+1$で定まる関数$f$」
となります.
しかし,ただ厳密には「関数$f(x)$」が誤りであるとは言っても,
- 短くて分かりやすい
- 場合によっては混乱の恐れもほぼない
- 関数に逐一$f,g,\dots$などと名前を付けなくてよい
などの理由から,「関数$x^2+1$」の書き方を使うこともあります.
“$f(x)$”を関数とも理解できるのは,$x$を具体的に指定していないためです.
数学では定義していない文字を使うのは本来ご法度ですが,「関数$f(x)$」といえば暗黙のうちに「$x$を変数とする」と理解する慣習があるので,「関数$f(x)$」と書いても関数として理解できるわけですね.
関数列$\{f_n\}$と数列$\{f_n(x)\}$の違い
とはいえ,例えば関数列では関数の書き方を注意したい場合も多いです.
集合$A$上で定義された関数$f_1,f_2,f_3,\dots$を$\{f_n\}_{n=1}^{\infty}$や単に$\{f_n\}$と表し,$A$上の関数列という.
例えば,実数全部の集合$\R$上の関数列$\{f_n\}$を
\begin{align*}f_n(x)=\frac{1}{1+x^n}\end{align*}
とすると,$f_1,f_2,f_3,\dots$は次のようなグラフを持つ関数ですね.
上でも説明したように$f_n(x)$は$f_n$の$x$における「値」ですから,厳密には$\{f_n(x)\}$は関数列ではなく数列の意味になってしまいます.例えば,
\begin{align*}f_1(2)=\frac{1}{3},\ f_2(2)=\frac{1}{5},\ f_3(2)=\frac{1}{9}\end{align*}
なので,$\{f_n(2)\}$が数列$\frac{1}{3},\frac{1}{5},\frac{1}{9},\dots$を表しているのと同じですね.
関数列と数列については扱いが異なることも多いです(例えば,「関数列の収束」と「数列の収束」は明確に定義が異なります)から,
- 関数列$\{f_n\}$
- ($x$をどこかに固定した)数列$\{f_n(x)\}$
のどちらで話をしているのかはしっかり区別したいところです.
関数列の収束には各点収束,一様収束などさまざまな極限がありますね.
$x$を変数と思って$\{f_n(x)\}$を関数列の意味で使う場合には,「関数列$\{f_n(x)\}$」などと関数列とみなしていることを明示するのが混乱の恐れがなくて良いでしょう.

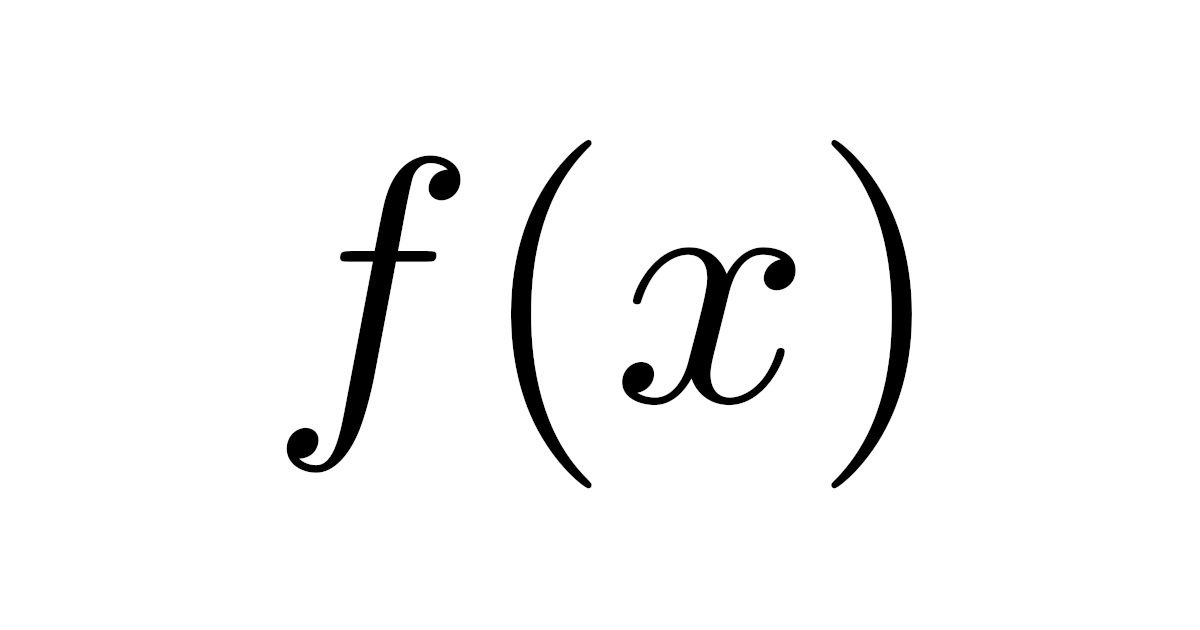
コメント