well-definedを理解する｜三角比の定義から具体例に考える

集合論
2021.01.26
集合論

数学でなんらかの定義をするとき，「well-defined性」を意識することは大切です．

大雑把にいえば，ある定義がwell-definedであるとは

  • その定義が機能する場合が存在する
  • その定義が矛盾していない

ということを指します．

と書くのは簡単ですが，どうやって定義が矛盾しないことを確認する必要があるのか，最初はすぐにはピンときませんね．

この記事では，具体的に「三角比の定義」を用いてwell-defined性の考え方を説明します．

well-definedとは

冒頭で書いたこととと重複しますが，定義がwell-definedであるとは次の２つを満たすことをいいます．

  1. その定義が機能する場合がある
  2. その定義が矛盾しない

また，well-definedでないことをill-defineといいます．

まずはこの２つを簡単に説明します．

条件１

たとえば

「２つの内角が$90^\circ$以上の三角形を超鈍角三角形という」

という定義をしたとしましょう．

しかし，三角形の内角の和は$180^\circ$なのでこのような三角形は存在しませんから，この「超鈍角三角形」の定義は意味がないことになります．

このように何かを定義するとき，その定義を満たすようなものが存在するというのが，定義がwell-definedであることの１つ目の条件です．

条件２

もう１つ定義において重要なことは，その定義が矛盾していないということです．

たとえば

「有理数$\frac{q}{p}$ ($p$, $q$は整数，$p\neq0$)を与えると，整数$p+q$を返す関数を$f$とする」

という定義をしたとしましょう．つまり，関数$f:\Q\to\Z$を

   \begin{align*} f\bra{\frac{q}{p}}=p+q\quad(p,q\in\Z,p\neq0) \end{align*}

で定義したとします．

しかし，この$f$は

   \begin{align*} 6=2+4=f\bra{\frac{2}{4}}=f\bra{\frac{1}{2}}=1+2=3 \end{align*}

となりますから，$6=3$となって矛盾しています．

この矛盾は$\frac{1}{2}$と$\frac{2}{4}$が同じ値であるにも関わらず，$f$によって返される値が異なってしまっているのが原因です．

このように，($\frac{1}{2}$と$\frac{2}{4}$のように)同じものでも複数の形が考えられるときに，どちらでも同じものが返ってこないと関数は矛盾を引き起こしてしまいます．

このような矛盾が起きないというのが，well-definedの２つ目の条件です．

well-definedの例

具体例として，三角比の定義がwell-definedであることを確かめましょう．

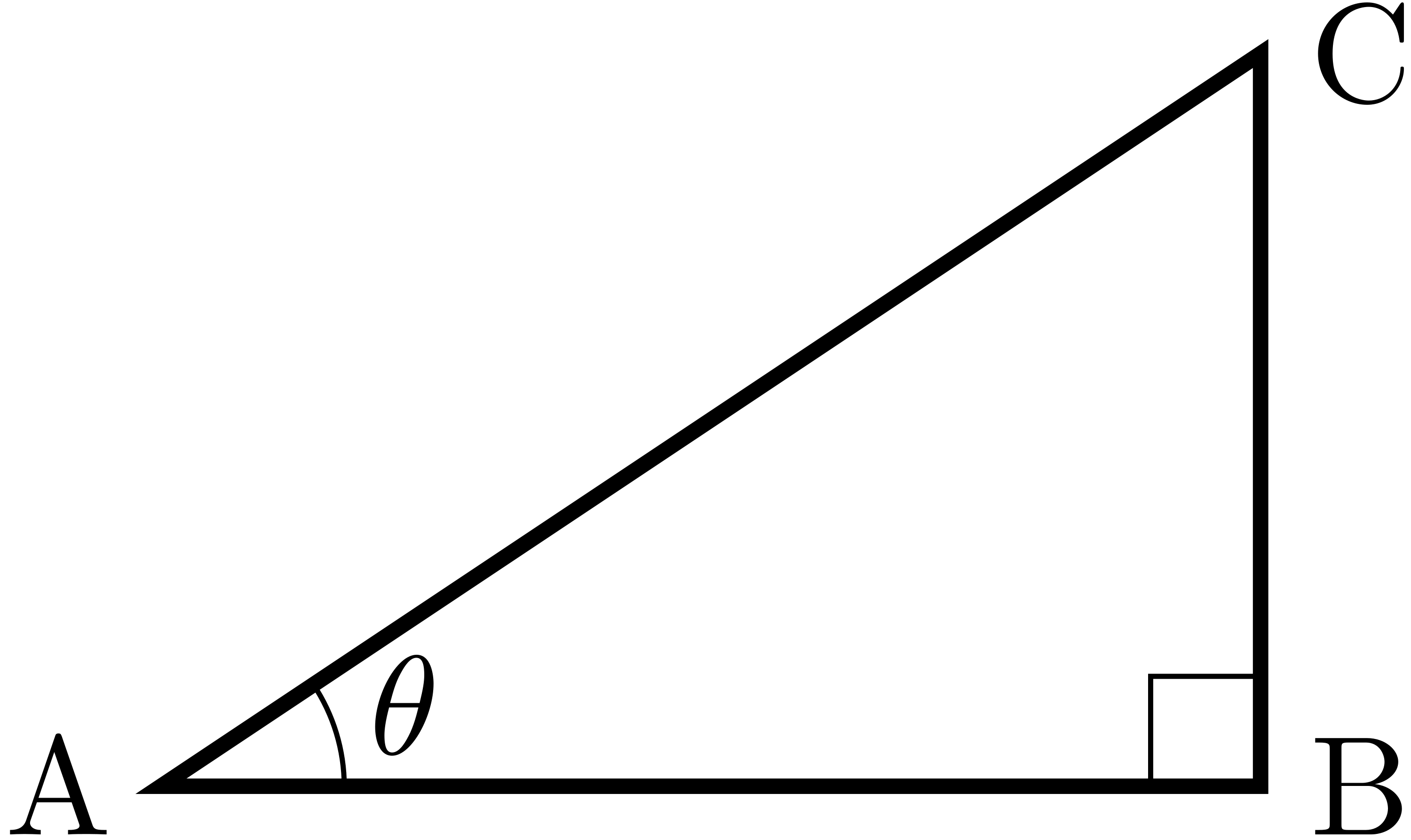
$\ang{B}=90^{\circ}$を満たす直角三角形ABCを考える．$\theta=\ang{A}$とする．

Rendered by QuickLaTeX.com

このとき，実数$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を

   \begin{align*} \sin{\theta}=\frac{\mrm{BC}}{\mrm{AC}},\quad \cos{\theta}=\frac{\mrm{AB}}{\mrm{AC}},\quad \tan{\theta}=\frac{\mrm{CB}}{\mrm{AB}} \end{align*}

と定める．

「$\ang{B}=90^{\circ}$を満たす直角三角形ABC」はもちろん存在するので，well-definedの１つ目の条件「定義が機能する場合がある」は満たしていますね．

よって，あとは２つ目の条件「定義が矛盾しない」を確かめればよいですね．

この定義における「$\ang{B}=90^{\circ}$を満たす直角三角形ABC」は１つに決まるわけではなく，様々な大きさのものが考えられます．

Rendered by QuickLaTeX.com

よって，

  • 大きい直角三角形ABCにおける$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$
  • 小さい直角三角形ABCにおける$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$

が違っていては定義が矛盾することになります．

しかし，それは２つの直角三角形

  • $\ang{B}=90^\circ$, $\theta=\ang{A}$を満たす$\tri{ABC}$
  • $\ang{B’}=90^\circ$, $\theta=\ang{A’}$を満たす$\tri{A’B’C’}$

は二角相等(２つの角がそれぞれ等しい)により相似なので

   \begin{align*} \dfrac{\mrm{BC}}{\mrm{AC}}=\dfrac{\mrm{B'C'}}{\mrm{A'C'}},\quad \dfrac{\mrm{AB}}{\mrm{AC}}=\dfrac{\mrm{A'B'}}{\mrm{A'C'}},\quad \dfrac{\mrm{CB}}{\mrm{AB}}=\dfrac{\mrm{C'B'}}{\mrm{A'B'}} \end{align*}

が成り立つため，「大きい直角三角形ABC」だろうが「小さい直角三角形ABC」だろうが$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$は等しく矛盾しないことが分かります．

つまり，どんな大きさの三角形ABCで考えても$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$は$\theta$のみによって決まることが分かりました．

以上より，三角比はwell-definedといえますね．

コメント