$f(x)=ax$ ($a\in\R$)の形の関数$f:\R\to\R$は,任意の$x,y\in\R$に対して
\begin{align*}f(x+y)=f(x)+f(y)\end{align*}
を満たしますね.そこで,この記事では次の問題を考えましょう.
任意の$x,y\in\R$に対して等式
\begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\R)\end{align*}
をみたす関数$f:\R\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限るか?
実はハメル(Hamel)基底というものを用いれば,$f(x+y)=f(x)+f(y)$を満たすが$f(x)=ax$の形をしていない関数$f:\R\to\R$の存在を示すことができます.
なお,この関数方程式$f(x+y)=f(x)+f(y)$はコーシー(Cauchy)の関数方程式と呼ばれており,$f$が連続なら$f(x)=ax$の形のものに限ることが証明できます(この記事の最後に証明しています).
この記事では
- ハメル基底
- コーシーの関数方程式の解
を順に説明します.
ただし,ハメル基底の存在を示すには選択公理を必要とするため,この記事では選択公理を仮定します.
なお,コーシーの関数方程式を満たす関数$f$に連続性を課せば$f(x)=ax$に限ることが証明できます.これについては以下の記事を参照してください.
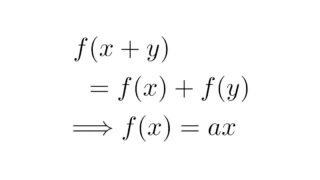
ハメル基底
まずはハメル基底を説明します.
次の[1], [2]を満たす$B\subset\R$をハメル基底という:
[1] 任意の有限個の$b_1,\dots,b_n\in B$に対して,
\begin{align*}r_1b_1+\dots+r_nb_n=0\quad (r_1,\dots,r_n\in\Q)\end{align*}
が成り立つなら$r_1=\dots=r_n=0$である.
[2] 任意の$x\in\R$に対して,$b_1,\dots,b_n\in B$と$r_1,\dots,r_n\in\Q$が存在して
\begin{align*}x=r_1b_1+\dots+r_nb_n\end{align*}
と表せる.
ハメル基底は体$\Q$上のベクトル空間$\R$の基底であるということができますね.
つまり,どんな実数も$B$の有限個の元の線形結合で表せる(かつ表し方が一通り)となる集合$B$をハメル基底というわけですね.
次の集合はハメル基底か?
- $\{1,\sqrt{2}\}$
- $\{1,\sqrt{2},\sqrt{3}\}$
(1)$\{1,\sqrt{2}\}$を基底とする有理数体$\Q$上(すなわち$\Q$係数)の線形空間を考える:
\begin{align*}\spn_{\Q}{(1,\sqrt{2})}=\set{x_1+x_2\sqrt{2}}{x_1,x_2\in\Q}.\end{align*}
このとき,例えば$\sqrt{3}$は$\spn_{\Q}{(1,\sqrt{2})}$に属さないので,$\{1,\sqrt{2}\}$はハメル基底ではない.
(2)$\{1,\sqrt{2},\sqrt{3}\}$を基底とする有理数体$\Q$上の線形空間を考える:
\begin{align*}\spn_{\Q}{(1,\sqrt{2},\sqrt{3})}:=\set{x_1+x_2\sqrt{2}+x_3\sqrt{3}}{x_1,x_2,x_3\in\Q}.\end{align*}
このとき,例えば$\log_{2}{3}$は$\spn_{\Q}{(1,\sqrt{2},\sqrt{3})}$に属さないので,$\{1,\sqrt{2},\sqrt{3}\}$はハメル基底ではない.
これら2つの例で考えたように$\{1,\sqrt{2}\}$や$\{1,\sqrt{2},\sqrt{3}\}$はハメル基底ではありませんが,基底をなす実数をどんどん増やして「$B$を基底とする$\Q$上のベクトル空間が$\R$となるようにうまく$B\subset\R$をとる」ことができれば,この$B$をハメル基底というわけですね.
このように考えると,具体的にハメル基底を構成するのは難しそうなことは感じて頂けると思います.
実際,ハメル基底の存在の証明にはツォルン(Zorn)の補題(選択公理)を用いるため,存在することは証明できるものの具体的にハメル基底をとってくることは困難です.
選択公理を仮定すれば,ハメル基底は存在する.
ハメル基底の存在の証明について詳しくは以下の記事を参照してください.

$f(x+y)=f(x)+f(y)$をみたす関数
冒頭の問題の反例を挙げる前に,2つ考察しましょう.
考察1
実は関数$f$の定義域を$\R$ではなく$\Q$とすれば,$f(x)=ax$の形のものに限ることが証明できます.
つまり,次が成り立ちます.
任意の$x,y\in\Q$に対してコーシーの関数方程式
\begin{align*}f(x+y)=f(x)+f(y)\end{align*}
をみたす関数$f:\Q\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限る.
関数$f$の定義域が$\R$から$\Q$に変わっただけですが,この場合には$f(x)=ax$ ($a\in\R$)に限ります.
- 任意の$p\in\Z$に対して,$f(p)=pf(1)$が成り立つことを示す
- 任意の$p\in\Z$, $q\in\Z\setminus\{0\}$に対して,$f(\frac{p}{q})=\frac{1}{q}f(p)$が成り立つことを示す
という2ステップで証明することができます.
この詳しい証明は冒頭でも紹介した以下の記事を参照してください.
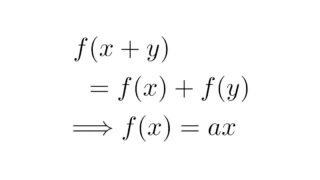
考察2
次の[問]を考えます.
[問] 任意の$x,y\in\spn_{\Q}{(1,\sqrt{2})}$に対して,$f(x+y)=f(x)+f(y)$をみたす関数$f:\spn_{\Q}{(1,\sqrt{2})}\to\R$は$f(x)=ax$ ($a\in\R$)に限るか.
この[問]では関数$f$の定義域が$\spn_{\Q}{(1,\sqrt{2})}$ですが,こうなると反例が存在します.
反例を挙げる.$f:\spn_{\Q}{(1,\sqrt{2})}\to\R$を
\begin{align*}f(x_1+x_2\sqrt{2})=x_1\quad(x_1,x_2\in\Q)\end{align*}
で定める.
このとき,$f(1)=1$, $f(\sqrt{2})=0$だから,$f$は$f(x)=ax$の形をしていない.
さらに,任意の$x,y\in\spn_{\Q}{(1,\sqrt{2})}$に対して,$x=x_1+x_2\sqrt{2}$, $y=y_1+y_2\sqrt{2}$ ($x_1,x_2,y_1,y_2\in\Q$)と表すと,
\begin{align*}f(x+y)
=&f((x_1+y_1)+(x_2+y_2)\sqrt{2})
\\=&x_1+y_1
\\=&f(x_1+x_2\sqrt{2})+f(y_1+y_2\sqrt{2})
\\=&f(x)+f(y)\end{align*}
となる.よって,この$f$が反例である.
上の補題から,ある$a_1\in\R$が存在して,任意の$x\in\Q$に対しては$f(x)=a_1x$が成り立ちます.
補題の証明と同様にすれば,ある$a_2\in\R$が存在して,任意の$x\in\Q$に対しては$f(\sqrt{2}x)=a_2(\sqrt{2}x)$が成り立つことも証明できます.
よって,この$a_1$と$a_2$が異なるようにとれば反例が構成できるわけですね.
上の解答例では$a_1=1$, $a_2=0$ととって反例になっています.
解答
それではこの記事の本題の次の問題を解きましょう.
任意の$x,y\in\R$に対してコーシーの関数方程式
\begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\R)\end{align*}
をみたす関数$f:\R\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限るか?
上の[問]の反例の構成を参考にすると,ハメル基底を用いることでには次のように反例が構成できることが分かります.
ハメル基底$B$を用いて反例を挙げる.$f:\R\to\R$を
\begin{align*}f\bra{x=\sum_i b_ix_i}=x_1\end{align*}
で定める.ただし,$b_1,b_2,\dots\in B$, $x_1,x_2,\dots\in\Q$である.
このとき,$f(b_1)=1$, $f(b_2)=0$だから,$f$は$f(x)=ax$の形をしていない.
また,任意の$x,y\in\R$に対して,有限和で$x=\sum_i b_ix_i$, $y=\sum_i b_iy_i$ ($x_i,y_i\in\Q$)と表すと,
\begin{align*}f(x+y)
=&f\bra{\sum_i b_i(x_i+y_i)}
\\=&x_1+y_1
\\=&f\bra{\sum_i b_ix_i}+f\bra{\sum_i b_iy_i}
\\=&f(x)+f(y)\end{align*}
となる.よって,この$f$が反例である.
先ほどの[問]と同じく,$a_1,a_2,\dots\in\R$とし,$f:\R\to\R$を
\begin{align*}f\bra{\sum_i b_ix_i}=\sum_i a_i(b_ix_i)\end{align*}
で定めるとき,$f$が$f(x)=ax$の形になるためには$a_1=a_2=a_3=\dots$となることが必要十分なので,やはり反例が無数に存在することが分かります.
上の反例は$a_1=1$, $a_2=a_3=\dots=0$ととったものになっていますね.
類似の関数方程式
コーシーの関数方程式に類似の関数方程式として以下のものを考えることもよくあります.
- $f_1(x+y)=f_1(x)f_1(y)$
- $f_2(xy)=f_2(x)+f_2(y)$
- $f_2(xy)=f_3(x)f_3(y)$
ただし,$f_1:\R\to\R$, $f_2,f_3:\R_{+}\to\R$で,$\R_{+}$は正の実数全部の集合です.
これらの関数$f_1,f_2,f_3$が連続なら,ある$a\in\R$が存在して
- $f_1(x)=a^x$
- $f_2(x)=a\log{x}$
- $f_3(x)=x^a$
となることが証明できますが,連続と限らなければコーシーの関数方程式と同様に他の解が存在します.
実際,ハメル基底$B$を用いて
- $f_1(x)=2^{x_1}$ ($x=\sum_i b_ix_i$)
- $f_2(x’)=x_1$ ($x’=e^{x}$, $x=\sum_i b_ix_i$)
- $f_3(x’)=2^{x_1}$ ($x’=e^{x}$, $x=\sum_i b_ix_i$)
で定める($b_1,b_2,\dots\in B, x_1,x_2,\dots\in\Q$)と,上で挙げたものと異なる解となります.

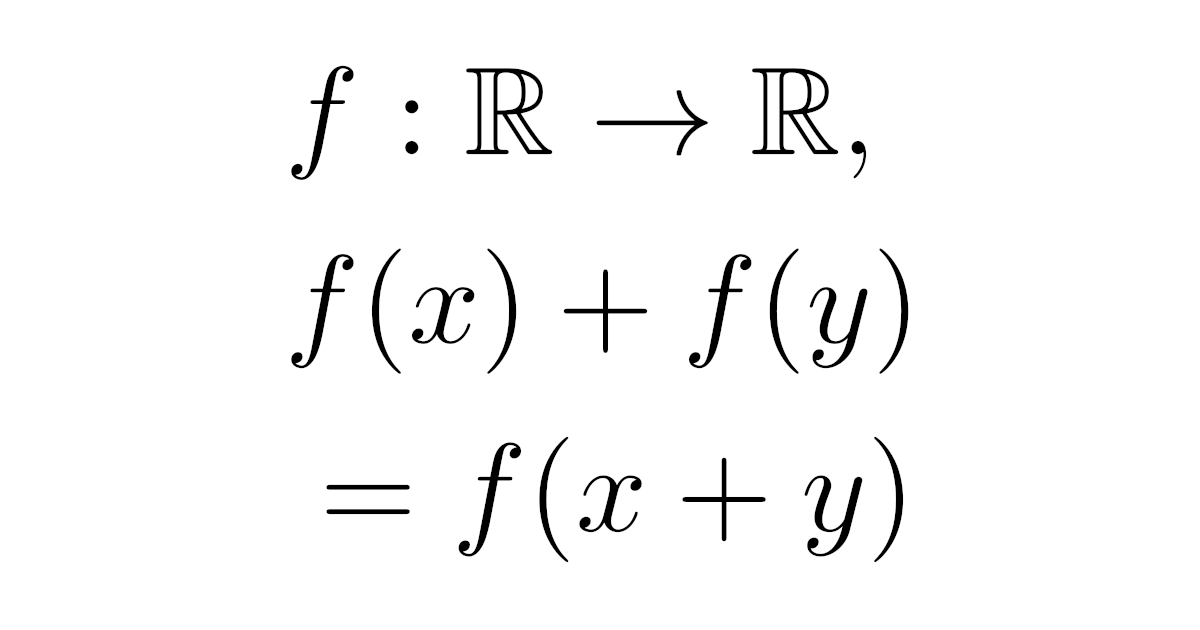
コメント