高校数学では「微分の逆演算」として積分を導入することが多いです.しかし,この方法では積分できる関数が限られるなどの不具合があります.
そこで微分積分学では,微分と無関係に定義されるリーマン積分$\dint_{a}^{b}f(x)\,dx$を学びます.リーマン積分は微分を全く用いずに定義されるものの,結局「連続関数に対しては微分と積分がある意味で逆演算になっている」という微分積分学の基本定理が成り立ちます.
この微分積分学の基本定理を用いると,リーマン積分を簡単に計算することができます.
この記事では
- 準備(不定積分と原始関数)
- 微分積分学の基本定理の主張と証明
- 参考文献
を順に解説します.
準備(不定積分と原始関数)
微分積分学の基本定理を説明するために,不定積分と原始関数が必要なので,まずはこれらの定義を確認しておきましょう.
リーマン積分は微分に無関係に定義される
不定積分の定義のために,まずはリーマン積分の定義を確認しておきましょう.
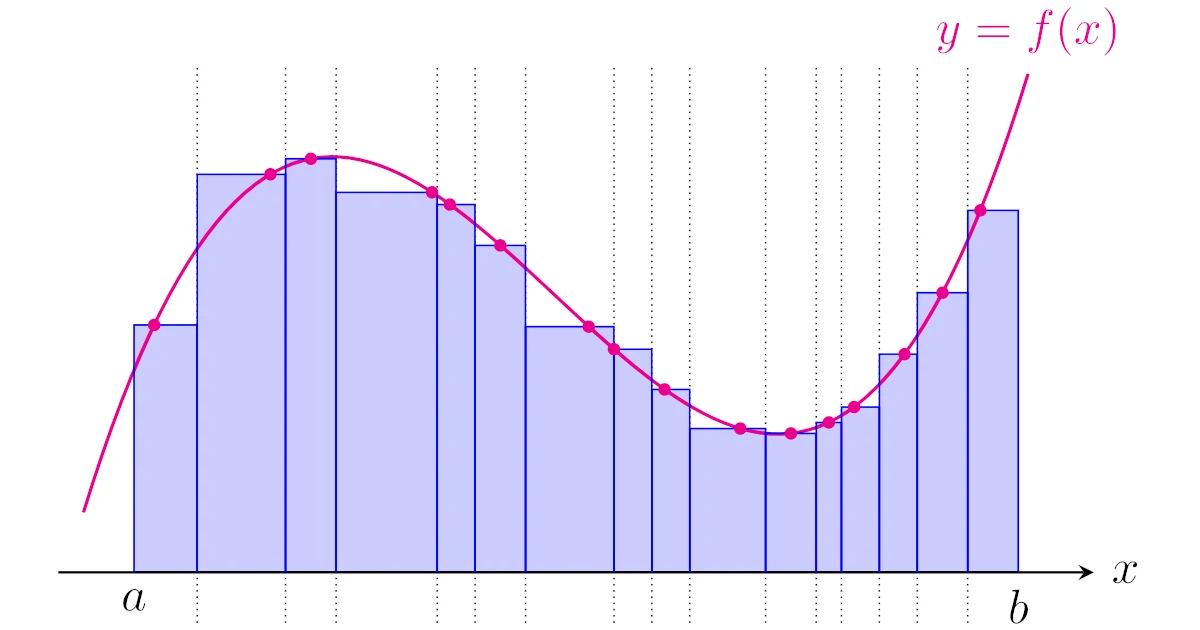
直観的には,$[a,b]$上で0以上の値を取る関数$f$のリーマン積分は
\begin{align*}y=f(x),\quad x=a,\quad x=b,\quad y=0\end{align*}
で囲まれた部分を長方形で近似する積分なのでした.
$M_n=\{1,2,\dots,n\}$とおく.関数$f:[a,b]\to\R$を考える.分割
\begin{align*}\Delta:a=x_0<x_1<\dots<x_n=b\end{align*}
に対して,$|\Delta|:=\max\limits_{i\in M_n}(x_i-x_{i-1})$とおく.また,$\xi_i\in[x_{i-1},x_i]$をとる($i\in M_n$).このとき,$f$が$[a,b]$上でリーマン積分可能であるとは,極限
\begin{align*}\lim_{|\Delta|\to0}\sum_{i=1}^{n}f(\xi_i)(x_i-x_{i-1})\end{align*}
が$\Delta$と$\xi_i$によらず一定の値に収束することをいい,このときのこの極限を$f$の$[a,b]$上のリーマン積分(Riemann integral)といい$\dint_{a}^{b}f(x)\,dx$と表す.
このリーマン積分の定義では微分が全く使われていないことが大切です.
なお,この定義での和$\sum\limits_{i=1}^{n}f(\xi_i)(x_i-x_{i-1})$をリーマン和というのでした.
不定積分も微分に関係なく定義される
リーマン積分が微分に無関係に定義されているので,リーマン積分から定義される次の不定積分も微分に関係なく定義されますね.
関数$f:[a,b]\to\R$は$[a,b]$上リーマン積分可能であるとし,$c\in[a,b]$とする.このとき,
\begin{align*}F(x)=\int_{c}^{x}f(t)\,dt\end{align*}
で定まる関数$F:[a,b]\to\R$を$f$の($c$から$x$までの)不定積分(indefinite integral)という.
定数$c\in[a,b]$のとり方によって不定積分$F$は異なりますが,$c$のとり方を変えても不定積分は定数差になります.実際,
- $c\in[a,b]$に対する$f$の不定積分を$F_{c}$
- $c’\in[a,b]$に対する$f$の不定積分を$F_{c’}$
とすると,定義から
\begin{align*}F_c(x)-F_{c’}(x)
=&\int_{c}^{x}f(t)\,dt-\int_{c’}^{x}f(t)\,dt
\\=&\int_{c}^{c’}f(t)\,dt\end{align*}
なので,$F_c(x)$と$F_{c’}(x)$の差は定数$\dint_{c}^{c’}f(t)\,dt$と分かりますね.
原始関数は微分を用いて定義される
関数$F$を微分して関数$f$になるとき,$F$を$f$の原始関数といいます.
$I\subset\R$を区間とする.関数$f:I\to\R$に対して,関数$F:I\to\R$が$F’=f$を満たすとき,$F$を$f$の原始関数という.
定義域の区間$I$が端点を含むとき,端点での微分係数は片側微分で考えています.
$f$の任意の原始関数に定数を加えてできる関数も$f$の原始関数です.実際,定数関数の導関数は恒等的に0な関数なので,$F$が$f$の原始関数であれば
\begin{align*}(F+C)’=f+0=f\end{align*}
となるので,$F+C$も$f$の原始関数ですね.
微分積分学の基本定理の主張と証明
それでは微分積分学の基本定理の説明に移ります.
微分積分学の基本定理は微分と積分の関係に関する定理
不定積分と原始関数の定義において
- 不定積分の定義には微分を用いない
- 原始関数の定義には積分を用いない
のでした.そのため,不定積分と原始関数の関係を述べることができれば,別々に定義されたはずの積分と微分に関係があることになりますね.
この関係を述べた定理が微分積分学の基本定理で,次の通りです.
[微分積分学の基本定理]$f$を区間$I=[a,b]\subset\R$上の実数値連続関数とする.このとき,次が成り立つ.
- $f$の不定積分は,$f$の原始関数である.
- $f$の原始関数$G$は,$f$の不定積分$F$と定数$C\in\R$を用いて$G(x)=F(x)+C$($x\in I$)と表せる.
- $f$の原始関数$G$に対して,$\dint_{a}^{b}f(t)\,dt=G(b)-G(a)$が成り立つ.
微分積分学の基本定理は「微積分の基本定理」「微分積分の基本定理」などと呼ぶことも多いです.
微分積分学の基本定理は連続関数に対して成り立つ定理です.高校数学で扱う関数はほとんどが連続関数であるため,高校数学では最初から積分を微分の逆演算として定義していても問題が生じないわけですね.
さて,この微分積分学の基本定理の3つのうち,
- 定理の(1)では不定積分は原始関数であること
- 定理の(2)では原始関数は不定積分の定数差のものだけであること
を保証しています.
また,本来の定義に従ってリーマン積分を求めようとすると,リーマン和の極限を計算しなくてはならず一般にはとても大変です.一方,原始関数は比較的簡単に得られることも多いです.定理の(3)はリーマン積分を定義から直接計算しなくても,比較的簡単に得られる原始関数から計算できるということを主張しているわけですね.
微分積分学の基本定理の証明
(1)不定積分が原始関数であることの証明
$I$上の不定積分$F$を$F(x)=\int_{c}^{x}f(t)\,dt$とする($c\in I$).
$f$は$I$上で連続だから,任意の$x\in I$と$\epsilon>0$に対して,ある$\delta>0$が存在して,$|t-x|<\delta$なら$|f(t)-f(x)|<\epsilon$を満たす.
よって,$x+h\in I$なる任意の$h\in(-\delta,\delta)\setminus\{0\}$に対して
\begin{align}&\abs{\frac{F(x+h)-F(x)}{h}-f(x)}\notag
\\&=\frac{1}{|h|}\abs{\bra{\int_{c}^{x+h}f(t)\,dt-\int_{c}^{x}f(t)\,dt}-hf(x)}\notag
\\&=\frac{1}{|h|}\abs{\int_{x}^{x+h}f(t)\,dt-\int_{x}^{x+h}f(x)\,dt}\notag
\\&=\frac{1}{|h|}\abs{\int_{x}^{x+h}(f(t)-f(x))\,dt}\label{eq:1/h}\tag{$*$}
\end{align}
となる.$h>0$のとき
\begin{align*}\eqref{eq:1/h}\le\frac{1}{h}\int_{x}^{x+h}|f(t)-f(x)|\,dt
<\frac{1}{h}\int_{x}^{x+h}\epsilon\,dt
=\frac{h\epsilon}{h}=\epsilon\end{align*}
$h<0$のとき
\begin{align*}\eqref{eq:1/h}\le\frac{1}{-h}\int_{x+h}^{x}|f(t)-f(x)|\,dt
<\frac{1}{-h}\int_{x+h}^{x}\epsilon\,dt
=\frac{-h\epsilon}{-h}=\epsilon\end{align*}
が成り立つから,$\lim\limits_{h\to0}\frac{F(x+h)-F(x)}{h}=f(x)$が得られた.すなわち,$I$上で$F$は微分可能で$F’=f$となるから,$F$は$I$上の$f$の原始関数である.
(2)原始関数が不定積分の定数差で表せることの証明
$G$は$f$の原始関数だから定義より$G’=f$であり,$F$は$f$の不定積分だから(1)より$F’=f$である.よって,
\begin{align*}F’=G’\iff (F-G)’=0\end{align*}
となるから$F-G$は定数なので,$G$は不定積分の定数差のものに限る.
(3)積分が原始関数で表せることの証明
(2)の記号を用いる.$F(x)=\dint_{a}^{x}f(t)\,dt$により不定積分$F$を定める.(2)より$F-G$は定数関数だったから
\begin{align*}F(x)-G(x)=F(a)-G(a)=-G(a)\end{align*}
である.ただし,最後の等式では$F(a)=\int_{a}^{a}f(t)\,dt=0$であることを用いた.よって
\begin{align*}\int_{a}^{b}f(t)\,dt=F(b)=G(b)-G(a)\end{align*}
が成り立つ.
証明に関する補足
(1)の証明について,いくつか簡単な補足をします.
補足1($x$は$t$の積分では定数扱い)
$f(x)$は$t$に無関係なので,$t$で積分すると
\begin{align*}hf(x)=\int_{x}^{x+h}f(x)\,dt\end{align*}
となります.$x$は積分変数$t$に無関係なので,$t$の積分において$x$は定数として扱ってもよいですね.
補足2(積分の絶対値の評価)
リーマン積分$\dint_{a}^{b}f(t)\,dt$の定義式は
\begin{align*}\lim_{|\Delta|\to0}\sum_{i=1}^{n}f(\xi_i)(x_i-x_{i-1})\end{align*}
という形でしたが,$x_i-x_{i-1}$の部分を$|x_i-x_{i-1}|$に置き換えたものを
\begin{align*}\int_{a}^{b}f(t)\,|dt|
:=\lim_{|\Delta|\to0}\sum_{i=1}^{n}f(\xi_i)|x_i-x_{i-1}|\end{align*}
とする記法があります.
この記法のもとでは$a,b\in\R$の大小関係が不明でも,
\begin{align*}\abs{\int_{a}^{b}f(t)\,dt}
\le\int_{a}^{b}|f(t)|\,|dt|\end{align*}
が成り立ちます.このことを用いると,(1)の証明では$h$の正負の場合分けをしなくても
\begin{align*}\abs{\frac{F(x+h)-F(x)}{h}-f(x)}
&\le\frac{1}{|h|}\int_{x}^{x+h}|f(t)-f(x)|\,|dt|
\\&<\frac{1}{|h|}\int_{x}^{x+h}\epsilon\,|dt|
=\frac{|h|\epsilon}{|h|}
=\epsilon\end{align*}
と評価できます.
参考文献
以下は参考文献です.
解析入門
[杉浦光男 著/東京大学出版会]
解析学の教科書としては非常に有名で,理論系で解析がしっかり必要となる人は持っておいてよいテキストです.
- 第1巻で1変数の微分積分学
- 第2巻で多変数の微分積分学
を扱っています.本書に対応した演習書「解析演習」も出版されています.
本書の特徴としては
- 数学的に厳密に書かれている
- 基本的な微分積分学の知識体系は網羅されている
の2点が挙げられます.
このため,辞書的に使う教科書という位置付けて持っている人も多いようです.
なお,この記事の内容は第1巻に載っています.
微分積分学
[笠原晧司 著/サイエンス社]
微分積分学の教科書として有名な名著です.
具体例を多く扱いイメージを掴むことに重点を置きつつ,議論もきっちりしているため,大学1年生の微分積分学をしっかり学びたい人には心強い味方になると思います.
具体例のレベルは基本的なものに加えて少々難しいものも含まれているので,いろいろな具体例に触れたい人は持っておいてもよいでしょう.
このため,しっかり数学をやりたい人の微分積分学の導入としてオススメできる一冊です.



コメント