関数$f$によっては
- 重積分$\dint_{\R^m\times\R^n}f(x,y)\,d(x,y)$
- 逐次積分$\dint_{\R^m}\bra{\dint_{\R^n}f(x,y)\,dy}\,dx$
が一致しないことがあります．
そこで，これら重積分と逐次積分が一致するための条件があれば嬉しいわけですが，ルベーグ積分においてこの十分条件を述べた定理としてフビニ（Fubini）の定理・トネリ（Tonelli）の定理があります．
また，フビニの定理とトネリの定理を組み合わせたフビニ-トネリの定理と呼ばれる定理もあります．
また，フビニの定理・トネリの定理・フビニ-トネリの定理を総称して「フビニの定理」と呼ぶことも多く，これらは解析学において非常に重要な定理です．
この記事では，フビニの定理・トネリの定理・フビニ-トネリの定理を概説します．
これらの定理は$\R^m$と$\R^n$より一般に$\sigma$-有限測度空間上の積分でも成り立ちますが，これについてはこの記事の最後に簡単に紹介するに留めます．
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
フビニの定理とトネリの定理
まずは$\R^m\times\R^n$上のルベーグ積分に関するフビニの定理とトネリの定理について解説します．
フビニの定理
フビニの定理は重積分可能なら重積分と逐次積分が一致するという定理です．
［フビニの定理１］関数$f:\R^m\times\R^n\to\overline{\R}$が$\R^m\times\R^n$上可積分であれば，$\R^m$上ほとんど至るところで$f(x,\cdot)$は$\R^n$上可積分で
\begin{align*}\int_{\R^m\times\R^n}f(x,y)\,d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}f(x,y)\,dy}\,dx\end{align*}
が成り立つ．ただし，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
「$\R^m\times\R^n$上の関数$f$が$\R^m\times\R^n$上可積分である」というのは，$f$が$\R^m\times\R^n$上可測であって
\begin{align*}\int_{\R^m\times\R^n}f(x,y)\,d(x,y)<\infty\end{align*}
が成り立つと言うことができます．
また，主張の中の
「$\R^m$上ほとんど至るところで$f(x,\cdot)$は$\R^n$上可積分」……$(*)$
は「$x\in\R^m$を固定するごとに$\R^n$の関数$f(x,\cdot)$が定まるが，$\R^m$上ほとんど至るところでこの$\R^n$の関数$f(x,\cdot)$を$\R^n$で積分した$\dint_{\R^n}f(x,y)\,dy$が存在する」という意味です．
定理の等式の右辺で$\dint_{\R^n}f(x,y)\,dy$を$\R^m$で積分する以上，$\dint_{\R^n}f(x,y)\,dy$が$\R^m$上ほとんど至るところで定義されている必要があるために，主張の中にこの$(*)$の記述があるわけですね．
以上をまとめると，フビニの定理は「$f$が$\R^m\times\R^n$上可積分であれば，累次積分$\dint_{\R^m}\bra{\int_{\R^n}f(x,y)\,dy}\,dx$が存在して，重積分$\dint_{\R^m\times \R^n}f(x,y)\,d(x,y)$と一致する」とも表現できますね．
また，以上で$\R^m$と$\R^n$の立場を入れ替えてもよく，結局次が成り立ちます．
［フビニの定理２］関数$f:\R^m\times\R^n\to\overline{\R}$が$\R^m\times\R^n$上可積分であれば，$\R^m$上ほとんど至るところで$f(x,\cdot)$は$\R^n$上可積分，かつ$\R^n$上ほとんど至るところで$f(\cdot,y)$は$\R^m$上可積分で
\begin{align*}\int_{\R^m\times\R^n}f(x,y)\,d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}f(x,y)\,dy}\,dx
=\int_{\R^n}\bra{\int_{\R^m}f(x,y)\,dx}\,dy\end{align*}
が成り立つ．ただし，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
トネリの定理
トネリの定理は非負なら重積分と逐次積分が一致するという定理です．
［トネリの定理］関数$f:\R^m\times\R^n\to\overline{\R}$が$\R^m\times\R^n$上可測かつ非負値であれば
\begin{align*}\int_{\R^m\times\R^n}f(x,y)\,d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}f(x,y)\,dy}\,dx
=\int_{\R^n}\bra{\int_{\R^m}f(x,y)\,dx}\,dy\end{align*}
が成り立つ．ただし，この等式は$\infty$をとる場合にも成り立ち，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
トネリの定理ではフビニの定理のような可積分性の条件を必要とせず，ただ$f$が可測かつ非負でさえあれば重積分と累次積分が一致することを主張しています．
先ほどのフビニの定理の説明における$(*)$に相当する記述がない理由は，非負可測関数の積分は$\infty$を許せば必ず存在することが理由です．
すなわち，$\dint_{\R^n}f(x,y)\,dy$は$\R^m$上至るところで($\infty$を許して)存在しますし，$\dint_{\R^m}f(x,y)\,dx$は$\R^n$上至るところで($\infty$を許して)存在します．
フビニ-トネリの定理
フビニの定理の欠点は重積分$\dint_{\R^m\times\R^n}|f(x,y)|\,d(x,y)$が有限であることを先に示さなければならないことにあります．しかし，多くの場合で重積分の計算は簡単でないため，この点でフビニの定理単体では使いにくいことがよくあります．
一方でトネリの定理の欠点は非負値関数に対してのみ有効であることにあります．
「これらのいいとこどりをしよう」というのがフビニ-トネリの定理です．
［フビニ-トネリの定理］関数$f:\R^m\times\R^n\to\overline{\R}$が$\R^m\times\R^n$上可測であれば
\begin{align*}\int_{\R^m\times\R^n}|f(x,y)|d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}|f(x,y)|dx}dx
=\int_{\R^n}\bra{\int_{\R^m}|f(x,y)|dx}dy\end{align*}
が成り立ち，この値が有限であれば
\begin{align*}\int_{\R^m\times\R^n}f(x,y)d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}f(x,y)dy}dx
=\int_{\R^n}\bra{\int_{\R^m}f(x,y)dx}dy\end{align*}
が有限の値で成り立つ．ただし，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
フビニ-トネリの定理はフビニの定理・トネリの定理から，次のようにして簡単に導くことができます．
$f$が可測関数なら，$|f|$は非負可測関数だから，トネリの定理より
\begin{align*}\int_{\R^m\times\R^n}|f(x,y)|d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}|f(x,y)|dy}dx
=\int_{\R^n}\bra{\int_{\R^m}|f(x,y)|dx}dy\end{align*}
が成り立つ．
また，この値が有限であるとすると，$|f|$が$\R^m\times\R^n$上可積分だから$f$は$\R^m\times\R^n$上可積分である．よって，フビニの定理より
\begin{align*}\int_{\R^m\times\R^n}f(x,y)d(x,y)
=\int_{\R^m}\bra{\int_{\R^n}f(x,y)dy}dx
=\int_{\R^n}\bra{\int_{\R^m}f(x,y)dx}dy\end{align*}
が成り立つ．
可測関数$f$に対しては$f$が可積分であることと$|f|$が可積分であることが同値なので，トネリの定理からフビニの定理が使えるようになるわけですね．
応用上，フビニ-トネリの定理は累次積分
- $\dint_{\R^m}\bra{\int_{\R^n}|f(x,y)|\,dy}\,dx$
- $\dint_{\R^n}\bra{\int_{\R^m}|f(x,y)|\,dx}\,dy$
のどちらかが計算でき，有限の値を持てば$f$の重積分と累次積分は一致する」として用いることが多いです．
直積測度空間
冒頭でも説明したように，フビニの定理・トネリの定理・フビニ-トネリの定理は\R^m\times\R^n上のみならず，$\sigma$-有限測度空間上で成り立ちます．
そこで，最後に$\sigma$-有限測度空間について簡単に説明します．
$\sigma$-有限測度空間と直積測度
$\sigma$-有限測度空間の定義は次の通りです．
［$\sigma$-有限測度空間］測度空間$(X,\mathcal{A},\mu)$が$\sigma$-有限であるとは，$\mathcal{A}$の列$\{X_k\}_{k=1}^{\infty}$が存在して，２条件
- 任意の$k\in\{1,2,\dots\}$に対して$\mu(X_k)<\infty$
- $X=\bigcup\limits_{k=1}^{\infty}X_k$
を満たすことをいう．
ルベーグ測度空間$(\R^n,\mathcal{L},\mu)$が$\sigma$-有限であることは
\begin{align*}Q_k:=[-k,k]^n\quad(k=1,2,\dots)\end{align*}
によって原点中心の一辺の長さが$2k$の超立方体$Q_k$を定めると，
- 任意の$k\in\{1,2,\dots\}$に対して$\mu(Q_k)=(2k)^n<\infty$
- $X=\bigcup\limits_{k=1}^{\infty}Q_k$
が成り立つことから分かります．
測度空間$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$に対して，$X$の可測部分集合$A$と$Y$の可測部分集合$B$の直積で生成される$\Omega:=X\times Y$の完全加法族を$\mathcal{F}$とします．
このとき，可測空間$(\Omega,\mathcal{F})$上の測度$P$で，任意の$A\in\mathcal{A}$, $B\in\mathcal{B}$に対して，$P(A\times B)=\mu(A)\nu(B)$となるものが存在します．
この$\mathcal{F}$, $P$をそれぞれ直積完全加法族，直積測度といい，測度空間$(\Omega,\mathcal{F},P)$を$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$の直積測度空間といいます
一般の測度空間に対してこの直積測度$P$が一意であるとは限りませんが，$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$がともに$\sigma$-有限測度空間であれば，$P$は一意に定まり，この$P$を$P=\mu\times\nu$と表します．
$\sigma$-有限測度空間を用いたフビニの定理たち
フビニの定理・トネリの定理・フビニ-トネリの定理を$\sigma$-有限測度空間$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$のもとで述べると以下のようになります．
［フビニの定理］測度空間$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$を$\sigma$-有限とする．関数$f:X\times Y\to\overline{\R}$が$X\times Y$上可積分であれば，$X$上ほとんど至るところで$f(x,\cdot)$は$Y$上可積分，かつ$Y$上ほとんど至るところで$f(\cdot,y)$は$X$上可積分で
\begin{align*}\int_{X\times Y}f(x,y)\,d(\mu\times\nu)
=\int_{X}\bra{\int_{Y}f(x,y)\,d\nu}\,d\mu
=\int_{Y}\bra{\int_{X}f(x,y)\,d\mu}\,d\nu\end{align*}
が成り立つ．ただし，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
［トネリの定理］測度空間$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$を$\sigma$-有限とする．関数$f:X\times Y\to\overline{\R}$が$X\times Y$上可測かつ非負であれば
\begin{align*}\int_{X\times Y}f(x,y)\,d(\mu\times\nu)
=\int_{X}\bra{\int_{Y}f(x,y)\,d\nu}\,d\mu
=\int_{Y}\bra{\int_{X}f(x,y)\,d\mu}\,d\nu\end{align*}
が成り立つ．ただし，この等式は$\infty$をとる場合にも成り立ち，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
［フビニ-トネリの定理］測度空間$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$を$\sigma$-有限とする．関数$f:X\times Y\to\overline{\R}$が$X\times Y$上可測であれば
\begin{align*}\int_{X\times Y}|f(x,y)|d(\mu\times\nu)
=\int_{X}\bra{\int_{Y}|f(x,y)|d\nu}d\mu
=\int_{Y}\bra{\int_{X}|f(x,y)|d\mu}d\nu\end{align*}
が成り立ち，この値が有限であれば
\begin{align*}\int_{X\times Y}f(x,y)\,d(\mu\times\nu)
=\int_{X}\bra{\int_{Y}f(x,y)\,d\nu}\,d\mu
=\int_{Y}\bra{\int_{X}f(x,y)\,d\mu}\,d\nu\end{align*}
が有限の値で成り立つ．ただし，$\overline{\R}$は拡大実数$\R\cup\{\pm\infty\}$である．
これらのうちフビニの定理は$\sigma$-有限測度空間上でなくとも成り立つことも知られていますが，ここでは以上の説明に留めます．
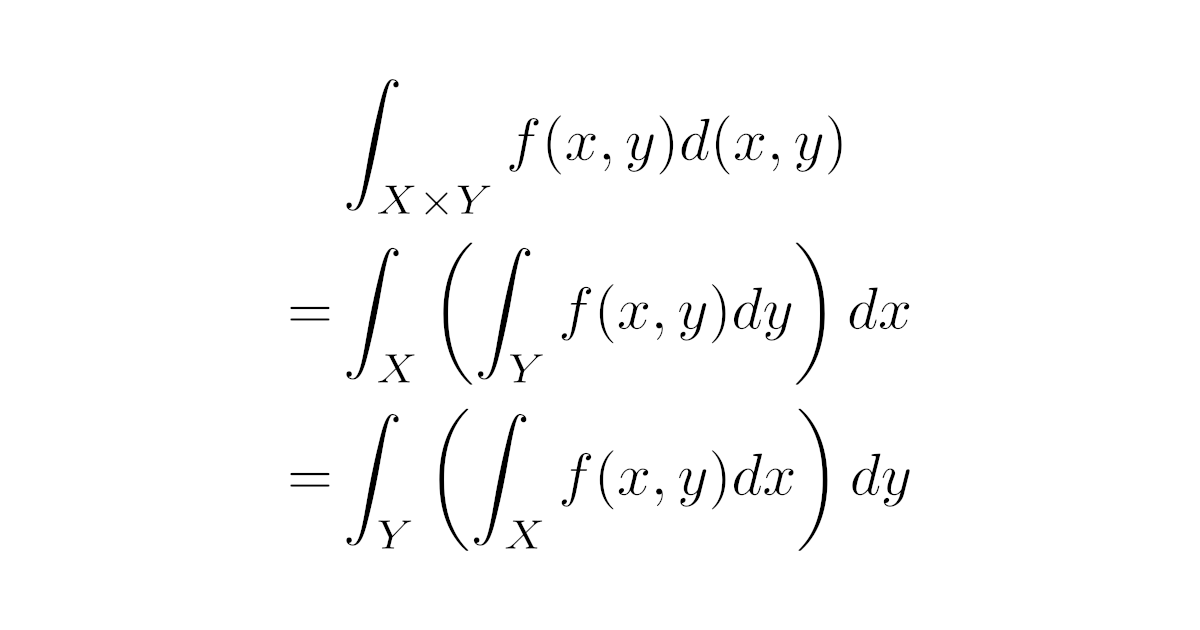
コメント