交項級数の定義と性質｜正負の項が交互に並ぶ級数の収束性

例えば，級数

$\begin{align*}1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\dots\end{align*}$

は正の項と負の項が交互に足されており，項の絶対値が（広義）単調減少して０に収束しています．

このような級数を交項級数（または交代級数）といい，交項級数は必ず収束することが知られています．

この記事では

交項級数の定義と性質
交項級数の性質の証明

を順に解説します．

交項級数の定義・具体例と性質
交項級数の性質の証明

交項級数の定義・具体例と性質

交項級数の定義を与え，具体例をいくつか考えましょう．そのあと，交項級数の基本的な性質についても解説します．

交項級数の定義・具体例

この記事の冒頭で述べたことをきちんと定義として書くと次のようになります．

正の項と負の項が交互に並んだ実数列$\{a_n\}$は，２つの条件

$|a_1|\ge|a_2|\ge|a_3|\ge|a_4|\ge\dots$
$\lim\limits_{n\to\infty}a_n=0$

をいずれも満たすとする．このとき，級数$\sum\limits_{n=1}^{\infty}a_n$は交項級数（alternating series）であるという．

正の項と負の項が交互に並ぶということは，任意の$n$に対して$a_na_{n+1}<0$が成り立つと言ってもいいですね．

全く同じことなので，次のように定義することもあります．

正項級数$\{a_n\}$は，２つの条件

$a_1\ge a_2\ge a_3\ge a_4\ge\dots$
$\lim\limits_{n\to\infty}a_n=0$

をいずれも満たすとする．このとき，級数$\sum\limits_{n=1}^{\infty}(-1)^{n}a_n$は交項級数（alternating series）であるという．

例えば，次の級数はいずれも交項級数です．

$1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dots$
$1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}-\dfrac{1}{\sqrt{4}}+\dfrac{1}{\sqrt{5}}-\dots$
$1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{9}-\dots$
$-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{8}-\dfrac{1}{10}+\dots$

いずれも正の項と負の項が交互に足されており，項の絶対値が（広義）単調減少して０に収束していることに注目してください．

性質１（交項級数の収束性）

級数が収束することの基本的な判定法として，次の定理を思い出しておきましょう．

絶対収束する級数は収束する．すなわち，実数列$\{a_n\}$が$\sum\limits_{n=1}^{\infty}|a_n|<\infty$を満たすとき，$\sum\limits_{n=1}^{\infty}a_n$は収束する．

しかし，絶対収束しない級数は収束することも収束しないこともあるため，絶対収束しない級数に対しては別の判定法が必要です．

そこで，交項級数の次の性質が役に立つことがあります．

交項級数は収束する．

絶対収束していなくても，交項級数であれば必ず収束するというわけですね．

たとえば，上で挙げた４つの交項級数

$1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dots$
$1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}-\dfrac{1}{\sqrt{4}}+\dfrac{1}{\sqrt{5}}-\dots$
$1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{9}-\dots$
$-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{8}-\dfrac{1}{10}+\dots$

はいずれも絶対収束しませんが，交項級数なので収束することが分かります．

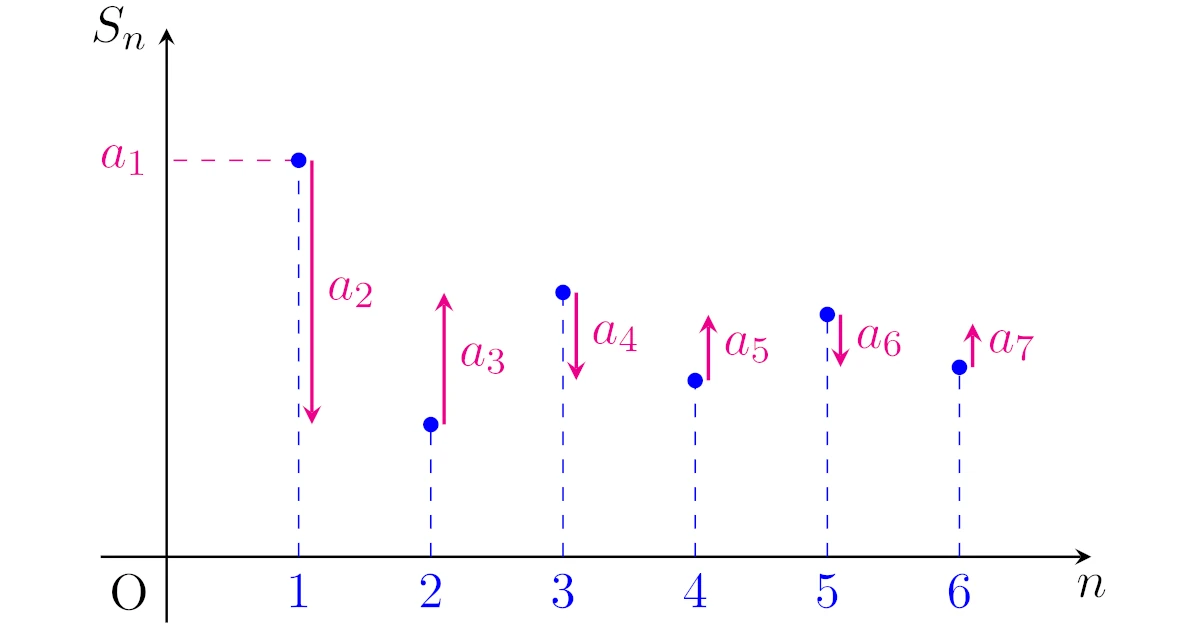
性質２（交項級数の部分和）

交項級数の極限と部分和について，次の不等式が成り立ちます．

$a_1>0$なる交項級数$S:=\sum\limits_{n=1}^{\infty}a_n$に対して，第$N$項までの部分和を$S_N$とおく：$S_n=\sum\limits_{n=1}^{N}a_n$．このとき

$\begin{align*}S_1\ge S_3\ge S_5\ge \dots\ge S\ge \dots\ge S_6\ge S_4\ge S_2\end{align*}$

が成り立つ．

一方，$a_1<0$なら不等式は全て逆向きとなります．

$a_1>0$（初項が正）なら，$S_1,S_3,S_5,\dots$は正の項までの和，$S_2,S_4,S_6,\dots$は負の項までの和なので，この命題の不等式は

正の項までの和は級数$S$より大きく，単調に減少する（$S_1\ge S_3\ge S_5\ge \dots\ge S$）
正の項までの和は級数$S$より小さく，単調に増加する（$S\ge \dots\ge S_6\ge S_4\ge S_2$）

ということを述べているわけですね．

交項級数では項が進むにつれ絶対値$|a_n|$が小さくなっていくので，部分和$S_n=\sum\limits_{k=1}^{n}a_k$の変化は小さくなっていきます．これにより，上記の不等式が成り立つわけですね．

交項級数の性質の証明

上で紹介した性質１と性質２は同時に証明することができます．

交項級数は収束する．$a_1>0$なる交項級数$S:=\dsum_{n=1}^{\infty}a_n$に対して，第$N$項までの部分和を$S_N$とおくと

$\begin{align*}S_1\ge S_3\ge S_5\ge \dots\ge S\ge \dots\ge S_6\ge S_4\ge S_2\end{align*}$

が成り立つ．

奇数番目の項は正で，偶数番目の項は負であることに注意する．

部分和の単調性を示す

正の整数$n$に対して，

$\begin{align*}|a_{2n}|\ge|a_{2n+1}|,\quad |a_{2n+1}|\ge|a_{2n+2}|\end{align*}$

なので，項の正負に注意すると

$\begin{align*}-a_{2n}\ge a_{2n+1},\quad a_{2n+1}\ge -a_{2n+2}\end{align*}$

となり，移項して

$\begin{align*}a_{2n}+a_{2n+1}\le 0,\quad a_{2n+1}+a_{2n+2}\ge 0\end{align*}$

が成り立つ．正の整数$n$に対して，

$\begin{align*}&S_{2n+1}-S_{2n-1}=a_{2n}+a_{2n+1}\le 0, \\&S_{2n+2}-S_{2n}=a_{2n+1}+a_{2n+2}\ge 0\end{align*}$

なので，$S_{2n+1}\le S_{2n-1}$, $S_{2n+2}\ge S_{2n}$が成り立つ．

$\{S_{2n-1}\}$と$\{S_{2n}\}$が収束することを示す

正の整数$n$に対して，

$\begin{align*}S_{2n-1}&=(a_1+a_2)+\dots+(a_{2n-3}+a_{2n-2})+a_{2n-1} \\&\ge a_{2n-1}>0, \\S_{2n}&=a_1+(a_2+a_3)+\dots++(a_{2n-2}+a_{2n-1})+a_{2n} \\&\le a_1+a_{2n}<a_1\end{align*}$

なので，$\{S_{2n-1}\}$は下に有界，$\{S_{2n-1}\}$は上に有界である．

先に示していた$\{S_{2n-1}\}$, $\{S_{2n}\}$の単調性と併せて，単調有界実数列の収束定理より極限

$\begin{align*}S_{+}:=\lim_{n\to\infty}S_{2n-1},\quad S_{-}:=\lim_{n\to\infty}S_{2n}\end{align*}$

が存在する．

ここで，$S_{2n}=S_{2n-1}+a_{2n}$の両辺で極限$n\to\infty$をとれば，交項級数の仮定$\lim\limits_{n\to\infty}a_n=0$と併せて$S_{-}=S_{+}$を得る．

交項級数が収束し，不等式を満たすことを示す

$S:=S_{-}(=S_{+})$とし，この$S$がもとの級数の極限であることを示す．

任意に$\epsilon>0$をとる．ある$N_1, N_2\in\N$が存在して，

$\begin{align*}&2n-1>N_1\Ra|S-S_{2n-1}|<\epsilon, \\&2n>N_2\Ra|S-S_{2n}|<\epsilon\end{align*}$

が成り立つから，$N_0:=\max\{N_1,N_2\}$とおくと，$n>N_0$のとき

$\begin{align*}|S-S_n|=\begin{cases}|S_{+}-S_{n}|&(n=1,3,5,\dots)\\|S_{-}-S_{n}|&(n=2,4,6,\dots)\end{cases}<\epsilon\end{align*}$

となる．よって，ε-N論法による極限の定義により，$\lim\limits_{n\to\infty}S_n=S$が成り立つ．

$\{S_{2n-1}\}$は単調減少だから$S_{2n-1}>S_{+}=S$が成り立ち，$\{S_{2n}\}$は単調増加だから$S_{2n}<S_{-}=S$が成り立つので，極限$S$は不等式も満たす．