2実変数$x,y$の実数値関数$f$の偏導関数のうち,
\begin{align*}f_{xy}\bra{=\frac{\partial^2 f}{\partial y\partial x}},\quad
f_{yx}\bra{=\frac{\partial^2 f}{\partial x\partial y}}\end{align*}
はいつでも等しいわけではありませんが,実用上の多くの場合で等しくなります.
この記事では
- 偏微分の順序交換が可能な条件
- 偏微分の順序交換が不可能な具体例
を順に解説します.
偏微分の順序交換が可能な条件
まずは2変数関数の場合を考えて,それをもとに3変数以上の場合を説明します.
2変数関数の場合の定理
$(a,b)\in\R^2$を内部に含む集合$U$を考える.2変数関数$f:U\to\R$が
- 点$(a,b)$の近くで$f_{xy}$, $f_{yx}$が存在
- $f_{xy}$, $f_{yx}$が点$(a,b)$で連続
をみたすとき,点$(a,b)$で偏微分の順序交換が可能である.すなわち,$f_{xy}(a,b)=f_{yx}(a,b)$が成り立つ.
いまの定理は点$(a,b)$での偏微分の順序交換が可能であるための条件を述べたものになっていますが,実用上は次のように集合上で用いることが多いです.
開集合$U\subset\R^2$を考える.2変数関数$f:U\to\R$が$U$上で$C^2$級であれば,$U$上の任意の点で偏微分の順序交換が可能である.すなわち,$f_{xy}=f_{yx}$が成り立つ.
多変数関数$f$が集合$U$上で$C^2$級であるとは「全ての2階偏導関数が存在して,それらが全て連続であること」でしたから,上の定理を$U$上の全ての点で考えれば,この系はすぐに得られますね.
具体例1(多項式)
2実変数$x,y$の多項式関数は全て$C^{\infty}$級ですから,上の系からいつでも偏微分の順序交換が可能となっているはずです.
このことを具体例で確かめてみましょう.
2実変数関数$f(x,y)=x+x^2y^3+y^4$について,計算により$f_{xy}=f_{yx}$を確かめよ.
偏微分の順番$f_{xy}=(f_x)_y$, $f_{yx}=(f_y)_x$に注意しましょう.
計算により
\begin{align*}f_x(x,y)=1+2xy^3,\quad
f_y(x,y)=3x^2y^2+4y^3\end{align*}
なので,
\begin{align*}f_{xy}(x,y)=6xy^2,\quad
f_{yx}(x,y)=6xy^2\end{align*}
である.確かに$f_{xy}=f_{yx}$が成り立つ.
具体例2($C^{\infty}$級関数)
他の関数でも考えてみましょう.
2変数関数$f:\R^2\to\R$を
\begin{align*}f(x,y)=x\cos{x}\sin{y}+y\sin{xy}\end{align*}
で定める.計算により$f_{xy}=f_{yx}$を確かめよ.
関数$f$は$C^{\infty}$級ですから,上の系からいつでも偏微分の順序交換が可能となっているはずです.このことを確かめる問題ですね.
計算により
\begin{align*}&f_x(x,y)=\cos{x}\sin{y}-x\sin{x}\sin{y}+y^2\cos{xy},
\\&f_y(x,y)=x\cos{x}\cos{y}+\sin{xy}+xy\cos{xy}\end{align*}
なので,
\begin{align*}f_{xy}(x,y)&=\cos{x}\cos{y}-x\sin{x}\cos{y}+2y\cos{xy}-xy^2\sin{xy},
\\f_{yx}(x,y)&=\cos{x}\cos{y}-x\sin{x}\cos{y}+y\cos{xy}+y\cos{xy}-xy^2\sin{xy}
\\&=\cos{x}\cos{y}-x\sin{x}\cos{y}+2y\cos{xy}-xy^2\sin{xy}\end{align*}
である.確かに$f_{xy}=f_{yx}$が成り立つ.
2変数関数の場合の証明
それでは上の定理を証明しておきましょう.
(再掲)$(a,b)\in\R$を内部に含む集合$U$を考える.2変数関数$f:U\to\R$が
- 点$(a,b)$の近くで$f_{xy}$, $f_{yx}$が存在
- $f_{xy}$, $f_{yx}$が点$(a,b)$で連続
をみたすとき,点$(a,b)$で偏微分の順序交換が可能である.すなわち,$f_{xy}(a,b)=f_{yx}(a,b)$が成り立つ.
十分0に近い実数$h_1,h_2\neq0$と十分$(a,b)$に近い実数の組$(x,y)$に対して,
\begin{align*}&p(x):=f(x,b+h_2)-f(x,b),
\\&q(x):=f(a+h_1,y)-f(a,y)\end{align*}
とおく.このとき,平均値の定理より,ある$\theta_1,\theta_2\in(0,1)$が存在して
\begin{align*}\frac{p(a+h_1)-p(a)}{h_1h_2}
&=\frac{p_x(a+\theta_1 h_1)}{h_2}
\\&=\frac{f_x(a+\theta_1 h_1,b+h_2)-f_x(a+\theta_1 h_1,b)}{h_2}
\\&=(f_x)_y(a+\theta_1 h_1,b+\theta_2 h_2)\end{align*}
が成り立つ.同様に,ある$\phi_1,\phi_2\in(0,1)$が存在して
\begin{align*}\frac{q(b+h_2)-q(b)}{h_1h_2}
=(f_y)_x(a+\phi_1 h_1,b+\phi_2 h_2)\end{align*}
が成り立つ.いま$p(a+h_1)-p(a)=q(b+h_2)-q(b)$なので,
\begin{align*}f_{xy}(a+\theta_1 h_1,b+\theta_2 h_2)
=f_{yx}(a+\phi_1 h_1,b+\phi_2 h_2)\end{align*}
が成り立ち,両辺で$h_1,h_2\to0$とすると,$f_{xy}$, $f_{yx}$の点$(a,b)$での連続性より
\begin{align*}f_{xy}(a,b)=f_{yx}(a,b)\end{align*}
が成り立つ.
3変数以上の関数の場合の定理
3変数以上の場合も2変数と同様に証明できるので,上で紹介した2変数の場合に対応する定理と系を紹介します.
$\m{a}\in\R^n$を内部に含む集合$U$を考え,異なる$k,\ell\in\{1,2,\dots,n\}$をとる.$n$変数関数$f:U\to\R$が
- 点$\m{a}$の近くで$\dfrac{\partial^2 f}{\partial x_k \partial x_\ell}$, $\dfrac{\partial^2 f}{\partial x_\ell \partial x_k}$が存在
- $\dfrac{\partial^2 f}{\partial x_k \partial x_\ell}$, $\dfrac{\partial^2 f}{\partial x_\ell \partial x_k}$が点$\m{a}$で連続
をみたすとき,$\dfrac{\partial^2 f}{\partial x_k \partial x_\ell}(\m{a})=\dfrac{\partial^2 f}{\partial x_\ell \partial x_k}(\m{a})$が成り立つ.
開集合$U\subset\R^n$上の実数値関数$f$が$U$上で$C^2$級であれば,任意の異なる$k,\ell\in\{1,2,\dots,n\}$に対し,$U$上の任意の点で$\dfrac{\partial^2 f}{\partial x_k \partial x_\ell}=\dfrac{\partial^2 f}{\partial x_\ell \partial x_k}$が成り立つ.
偏微分の順序交換が不可能な具体例
ある程度滑らかな関数では偏微分の順序は気にしなくてもよいわけですが,裏返せば滑らかでない関数は偏微分の順序交換ができないことがあるということになりますね.
そのような例を紹介します.
関数数$f:\R^{2}\to\R$を
\begin{align*}f(x,y)=\begin{cases}\dfrac{x^{3}y}{x^{2}+y^{2}}&(x,y)\neq(0,0),\\0&(x,y)=(0,0)\end{cases}\end{align*}
で定めると,$f_{xy}(0,0)\neq f_{xy}(0,0)$であることを示せ.
点$(0,0)$では場合分けで関数$f$が定義されているので,1階導関数も場合分けで求める必要があることに注意しましょう.
計算により示す.
1階導関数の計算
$\R^2$上の1階導関数$f_{x}$, $f_{y}$を求める.$(x,y)\neq(0,0)$において,
\begin{align*}f_{x}(x,y)
=\frac{3x^{2}y(x^{2}+y^{2})-x^{3}y\cdot2x}{(x^{2}+y^{2})^{2}}
=\frac{x^{4}y+3x^{2}y^{3}}{(x^{2}+y^{2})^{2}}\end{align*}
である.また,定義より
\begin{align*}f_{x}(0,0)=\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h}=0\end{align*}
である.すなわち,
\begin{align*}f_{x}(x,y)=\begin{cases}\dfrac{x^{4}y+3x^{2}y^{3}}{(x^{2}+y^{2})^{2}}&(x,y)\neq(0,0),\\0&(x,y)=(0,0)\end{cases}\end{align*}
である.同様に
\begin{align*}f_{y}(x,y)=\begin{cases}\dfrac{x^{5}-x^{3}y^{2}}{(x^{2}+y^{2})^{2}}&(x,y)\neq(0,0),\\0&(x,y)=(0,0)\end{cases}\end{align*}
である.
2階偏導関係数の計算
次に2階偏導関係数$f_{xy}(0,0)$, $f_{yx}(0,0)$を求める.
\begin{align*}&f_{xy}(0,0)=\lim_{h\to0}\frac{\pd{f}{x}(0,h)-\pd{f}{x}(0,0)}{h}=0,
\\&f_{yx}(0,0)=\lim_{h\to0}\frac{f_{y}(h,0)-f_{y}(0,0)}{h}
=\lim_{h\to0}\frac{\frac{h^{5}}{h^{4}}}{h}=1\end{align*}
となるので,$f_{xy}(0,0)\neq f_{yx}(0,0)$が得られました.

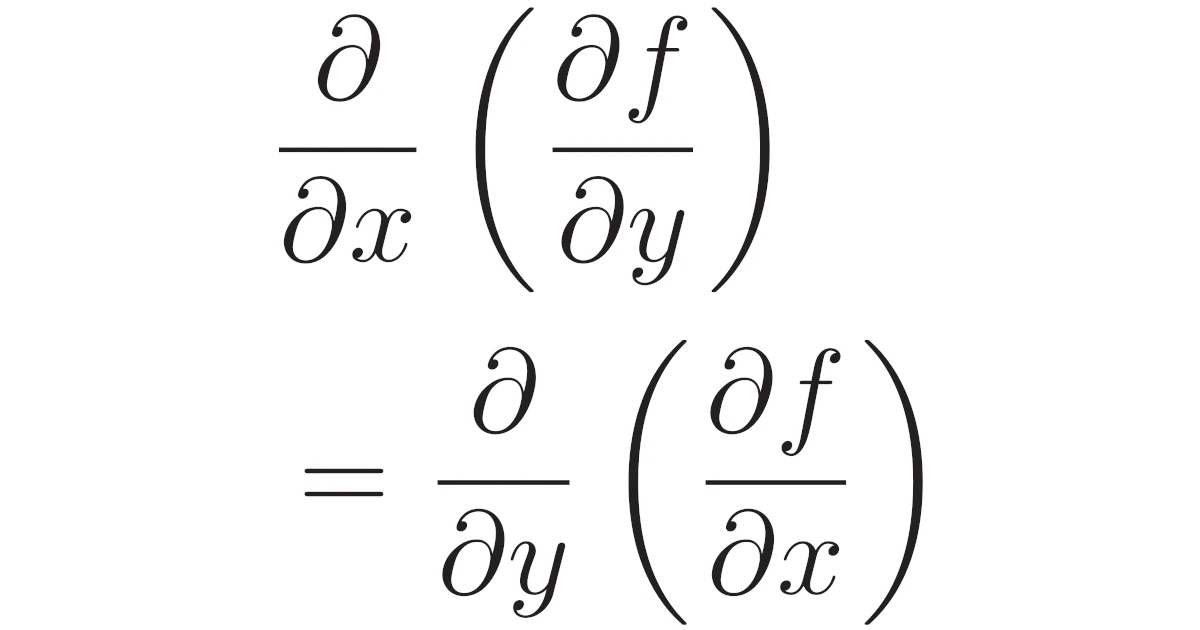
コメント