代数学で群論を学ぶと，そのうち剰余群を学ぶことになりますが，剰余群の定義で戸惑ってしまう人は多いように思います．
この戸惑う根底にあるのはwell-defined性と思われます．
剰余群の定義においてだけではなく数学全体においてwell-defined性は非常に重要ですが，高校ではともかく大学でもその意味を教えてもらったことがない人も多いように思います．
少なくとも私は教わったことがありません．
剰余群を定義する際にこのwell-defined性を理解していないと，「どうしてこんな議論が必要なのか」と思ってしまうことが多いようです．
本記事では，剰余群の定義を通してwell-defined性を理解することを目標とします．
目次
well-defined
まずは，well-defineについて説明します．
well-definedとは
定義がwell-definedであるとは，次の２つが成り立つことをいいます．
- その定義が機能する場合が存在する
- その定義が矛盾しない
また，well-definedでないことをill-defineといいます．
例えば，「１つの内角が$180^\circ$の三角形を超鈍角三角形という」という定義をしても，三角形の内角の和は$180^\circ$なのでこのような三角形は存在しません．
したがって，この定義はそもそも機能することがないので，ill-definedということになります．
well-definedの例
一方で，機能する場合があっても定義が矛盾するためにill-defindとなってしまうこともあります．
このことを，三角比の定義を例に考えます．
三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$は直角三角形を用いて以下のように定義されますね．
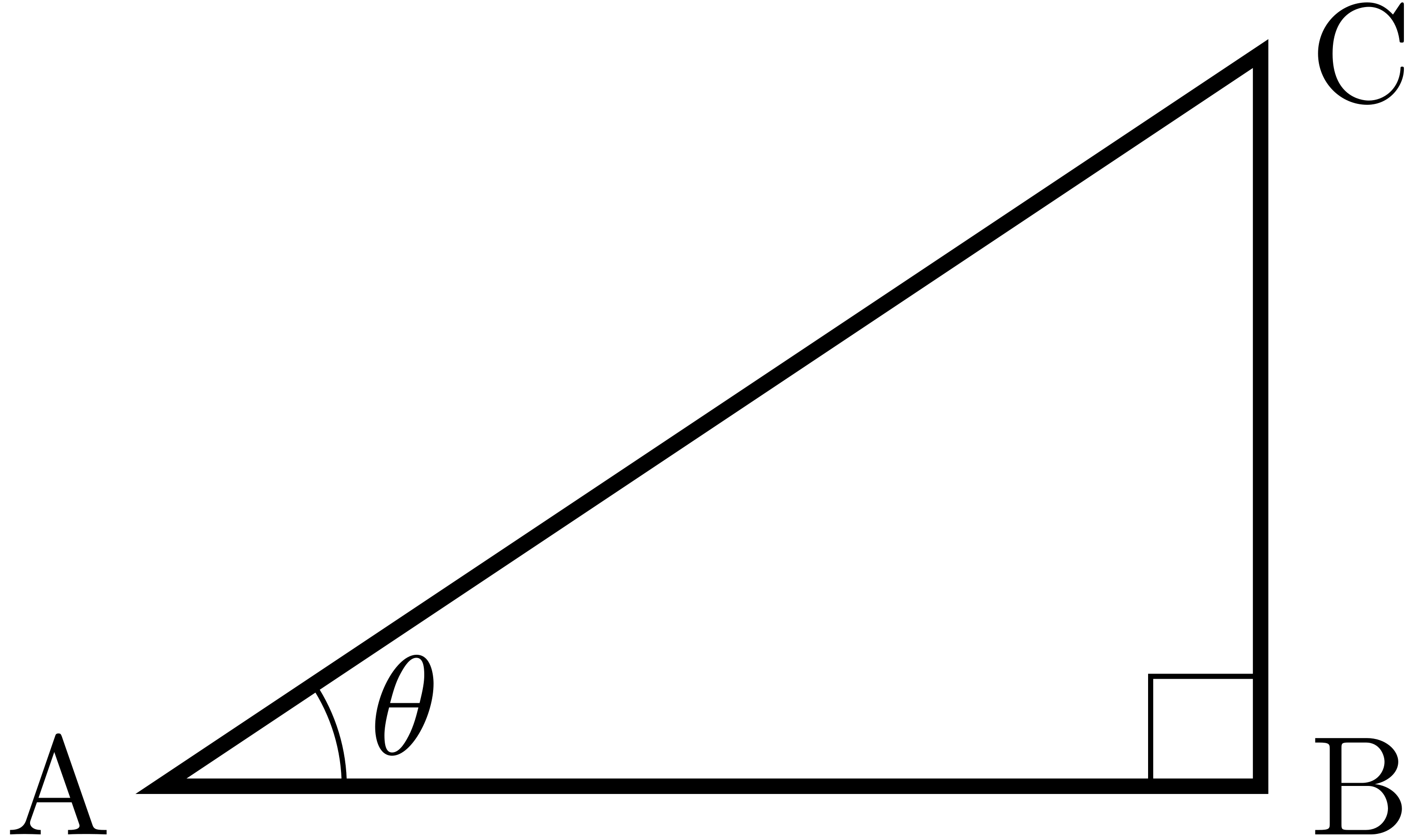
$\ang{B}=90^{\circ}$を満たす直角三角形ABCを考える．$\theta=\ang{A}$とする．
このとき，実数$\cos{\theta}$, $\sin{\theta}$, $\tan{\theta}$を
と定める．
この定義における「$\ang{B}=90^{\circ}$, $\theta=\ang{A}$を満たす直角三角形ABC」について，このような三角形は１つに決まるわけではなく，様々な大きさのものがあり得ます．
そのため
- 大きい直角三角形ABCにおける$\cos{\theta}$, $\sin{\theta}$, $\tan{\theta}$
- 小さい直角三角形ABCにおける$\cos{\theta}$, $\sin{\theta}$, $\tan{\theta}$
で値が変わってきては困ります．しかし，そんな心配はいりませんね．
それは２つの直角三角形
- $\ang{B}=90^\circ$, $\theta=\ang{A}$を満たす$\tri{ABC}$
- $\ang{B’}=90^\circ$, $\theta=\ang{A’}$を満たす$\tri{A’B’C’}$
は二角相等(２つの角がそれぞれ等しい)により相似なので
が成り立つからですね．
このように，上で見た三角比の定義では三角形ABCの大きさは自由ですが，どんな大きさの三角形ABCで考えても$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$は$\theta$のみによって$\cos{\theta}$, $\sin{\theta}$, $\tan{\theta}$の値が決まることになり矛盾しません．
このように，複数の対象(三角比の場合は様々な大きさの直角三角形)によって定義されうる場合には，どの対象で定義しても矛盾しないということが言えて初めてwell-definedと言えます．
このため，三角比はwell-definedと言えるわけですね．
可換群の剰余群
それでは，剰余群の定義の説明に移ります．
群は必ずしも可換ではありませんが，まずは比較的理解がしやすい可換群から説明します．
群の部分群による分解
$G:=\Z$は通常の和$+$により可換群となります．また，$N:=3\Z$ (３の倍数の集合)とすると，$N$は$G$の部分群となります．
このとき，集合として
となっていますね．ただし，$N$, $1+N$, $2+N$はそれぞれ
です．
このとき，群$N$からできた３つの集合$N$, $1+N$, $2+N$の集合を$G/N$と表します：
なお，$G/N=\{N,1+N,2+N\}$は集合の集合であるという点に注意してください．
さて，ここでのポイントは，$N$の集合の元全てに
- ３を足そうが
- ６を足そうが
- 12を足そうが
元がズレるだけで集合としては変わらないということです．つまり，
ということになります．同様に，
です．したがって，$G/N$は
などとも表すことができます．
なお，このときの$G/N=\{N,1+N,2+N\}$は商集合というものになっており，このとき元の１つ１つ$N$, $1+N$, $2+N$は同値類と呼ばれます．
これについては以下の記事を参照してください．
今の例で言えば，３で割ったあまりでグループ分けをしてできたものが$N$, $1+N$, $2+N$という見方ができます．このように数学的対象を「グループ分け」したいときには，集合論としては商集合を考えることになります．この記事では，「グループ分け」に相当する同値関係の考え方を説明し，商集合の考え方と具体例をみます．
可換群の剰余群の定義
ここで，いま見た例を少し一般化して，可換群についての剰余群の定義を確認しましょう．
[剰余群(可換群)] 演算$+$を備えた可換群$G$とその部分群$N$を考える．任意の$g_1,g_2\in G$に対して，$g_1+N,g_2+N\in G/N$の和$\dot{+}$を
で定めると，$G/N$は可換群となる．この群$G/N$を剰余群 (quotient group)という．
再び$G=\Z$, $N:=3\Z$として考えましょう．
この剰余群の定義は，例えば
のように，$G/N$の元の和を考えようということを述べています．
ここで，well-defined性が問題になります．
先ほど見たように，例えば$1+N=-2+N$と$3+N=9+N$が成り立つことから，$(1+N)+(3+N)$と$(-2+N)+(9+N)$は同じものの和なので，同じ結果になっているべきです．
実際に和を計算すると，
なので，これらは等しいですね．
このように，同じものについて複数の表し方ができてしまうので，異なる表し方でも結果が同じになっていることを確かめなければなりません．
この意味で，well-defined性が問題になっているわけです．
well-defined性の確認
それでは，可換群の剰余群の定義について，well-defined性を確認しましょう．
$G/N$の任意の２元$g_1+N$, $g_2+N$を考えます．
また，$g_1+N$, $g_2+N$はそれぞれ$h_1+N$, $h_2+N$とも書けるとしましょう．
このとき，$(g_1+N)\dot{+}(g_2+N)=(g_1+g_2)+N$と$(h_1+N)\dot{+}(h_2+N)=(h_1+h_2)+N$が同じ結果になることを示すことができれば，上の可換群の剰余群の定義がwell-definedであることが分かります．
$g_1+N=h_1+N$であることから$g_1-h_1\in N$が成り立ち，同様に$g_2-h_2\in N$が成り立ちます．
よって，$N$が群であることより，$(g_1-h_1)+(g_2-h_2)\in N$が成り立つので，$(g_1+g_2)-(h_1+h_2)\in N$が成り立ちます．
これにより$(g_1+g_2)+N=(h_1+h_2)+N$となり，確かに両者が等しいことが分かりました．
以上で，well-defined性が得られました．
一般の剰余群
最後に可換でない群に関して，剰余群を考えます．
正規部分群
可換でない剰余群を定義する際には，正規部分群の概念が不可欠です．
群$G$の部分群$N$が$G$の正規部分群 (normal subgroup)であるとは，任意の$g\in G$と$h\in N$に対して
が成り立つことをいう．
なお，$G$が可換なら，
となるので，$G$の任意の部分群$N$は正規部分群となります．
剰余群の定義
一般の群$G$とその部分群$N$に対して，$N$が正規部分群なら剰余類$G/H$は群となります．
[剰余群(一般)] 群$G$とその正規部分群$N$を考える．任意の$g_1,g_2\in G$に対して，$g_1N,g_2N\in G/N$の積を
で定めると，$G/N$は群となる．この群$G/N$を剰余群 (quotient group)という．
なお，可換群の剰余群を考えるときには単に「部分群」としていたのは，上述したように$G$が可換群であれば部分群$N$は必ず正規部分群になるからです．
可換とは限らない一般の群$G$の剰余群$G/N$を考える際には，必ず$N$は正規でなければなりません．
それでは，この一般の剰余群の定義について，well-defined性を証明して終わりにしましょう．
任意の$G/N$の２元$g_1N=h_1N$と$g_2N=h_2N$を考える．
なので，$n_1,n_2\in N$が存在して，$n_1=g_1{h_1}^{-1}$, $n_2=g_2{h_2}^{-1}$が成り立つ．よって，
が成り立つ．いま，$n_1\in N$であり，$N$は$G$の正規部分群だから$h_1n_2{h_1}^{-1}\in N$である．
よって，$n_1(h_1n_2{h_1}^{-1})\in N$だから$g_1g_2(h_1h_2)^{-1}\in N$が得られ，$(g_1g_2)N=(h_1h_2)N$が成り立つ．
以上より，$(g_1N)(g_2N)=(h_1N)(h_2N)$となって，well-defined性が従う．
また，剰余群を商集合を意識して考える場合には以下の記事のような説明もできます．
商集合は数学で分野を問わず様々な場面で用いられます．「商集合」を定義するには「同値関係」が必要で，同値関係とは「グループ分け」を数学的に定式化しただけで，発想自体は難しくありません．この記事では商集合の考え方を説明し，具体例として剰余群を挙げます．
参考文献
「代数学1 群論入門」(雪江明彦著，日本評論社)は群論の入門書である．
具体例が多く，行間が少ないため，初学者にも非常に読みやすい良著である．さらに，章末問題が豊富な上に解答の解説も非常に丁寧である．
章末問題のレベルもその賞で学んだ基本的な内容から，少し考える問題まで様々なので理解を深めるのに非常に便利である．
また，「群論入門」は予備知識をあまり仮定せず，必要事項を第1章にまとめてあり，1から独学で学ぶことができる点も嬉しい．
【参考記事：【書評】代数学1 群論入門(雪江明彦著，日本評論社)】
この本のレビューはこの記事を参照．代数学は抽象的な分野と言われるが，抽象を理解するためには具体の理解も大切なことは多い．本書は具体例が豊富なので，具体的なイメージから抽象化することができる．