[ローラン展開]はテイラー展開の進化形！留数定理の一歩前

$\alpha\in\C$に対して，複素関数$f$を

$\begin{align*} f(z)=c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots \end{align*}$

と表すとき，この右辺の級数を$f$の$\alpha$中心のテイラー(Taylor)展開というのでした．

前回の記事ではCauchyの積分公式を用いて$\alpha$の近くで正則な複素関数は$\alpha$中心でテイラー展開できることを説明しました．

一方，１点$\alpha$で複素関数$f$が微分可能でない場合には$f$を$\alpha$中心にテイラー展開することはできませんが，負冪の項$c_{-k}(z-\alpha)^{-k}$も用いて

$\begin{align*} f(z)=\dots+\frac{c_{-2}}{(z-\alpha)^2}+\frac{c_{-1}}{z-\alpha}+c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots. \end{align*}$

と表すことは可能で，この展開を$f$の$\alpha$中心のLaurent(ローラン)展開といいます．

また，上のLaurent展開の$-1$次の係数$c_{-1}$は$f$の$\alpha$での留数といい，この一連の記事の目標である留数定理に重要な役割を果たします．

この記事では

Laurent展開とは何か？
Laurent展開と留数
Laurent展開可能性と一意性の証明

を順に説明します．

「複素解析」の一連の記事はこちら

【複素解析１｜複素関数とは何か？図示の仕方も説明】
【複素解析２｜正則関数は超重要！複素関数の微分の考え方】
【複素解析３｜複素平面で積分しよう！複素積分の具体例も紹介】
【複素解析４｜超強力な[コーシーの積分定理]とその使い方】
【複素解析５｜縁の下の力持ち[コーシーの積分公式]を解説】
【複素解析６｜１回でも微分できれば[テイラー展開]できる！】
【複素解析７｜[ローラン展開]はテイラー展開の進化形！】←今の記事
【複素解析８｜[留数定理]を使って広義積分を計算する方法】

1 解説動画
2 テイラー展開
3 ローラン展開と留数
- 3.1 ローラン展開の定義と重要定理
- 3.2 留数
4 ローラン展開可能性と一意性の証明
- 4.1 ローラン展開可能性の証明
- 4.2 ローラン展開の一意性
5 留数定理
6 参考文献
- 6.1 [新装版]複素関数論の要諦

解説動画

この記事の解説動画をYouTubeにアップロードしています．

【複素解析⑦ローラン展開】テイラー展開の進化形！留数定理につながる重要な展開！

この動画が良かった方は是非チャンネル登録をお願いします！

テイラー展開

まずはTaylor展開について確認し，そのあとにTaylor展開と比較してLaurent展開を説明します．

領域$D\subset\C$上の正則関数は$D$上の任意の点を中心としてTaylor展開が可能で，詳しく述べると次のようになります．

[Taylor展開可能性]　複素平面上の領域$D$上の正則関数$f$と$\alpha\in D$を考え，周および内部が$D$に含まれる$\alpha$中心の円周$C$をとる．このとき，$f$は$C$の内部で

$\begin{align*} f(z)=c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots \end{align*}$

と表せる．すなわち，$f$は$\alpha$中心のTaylor展開が可能である．

領域$D$上の正則関数とは領域$D$上の全ての点で複素微分可能な複素関数のことでしたから，この定理から「領域$D$上で１回でも複素微分可能なら，$D$上の任意の点を中心としてTaylor展開可能」ということになります．

微分積分学のとき(実関数のとき)は少なくとも無限回微分可能でなければTaylor展開可能ではなかったことを思い出すと，複素解析のTaylor展開はとても簡単に成り立っていることが分かりますね．

複素解析のTaylor展開について詳しくは前回の記事を確認してください．

【前回の記事：複素解析６｜１回でも微分できれば[テイラー展開]できる！】

正則関数がTaylor展開可能であることはCauchyの積分公式から導くことができます．また，正則関数がTaylor展開可能であることを使えば，領域上で１回でも微分可能な複素関数は無限回微分可能であることも証明できます．

ローラン展開と留数

もし領域$D$上の１点$\alpha$での$f$の微分可能性が分からない場合はLaurent(ローラン)展開を考えることができます．

ローラン展開の定義と重要定理

$\alpha\in\C$に対して，複素平面上の領域$\alpha$を除くある領域上で関数$f$が

$\begin{align*} f(z)=&\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots \\\Bigl(=&\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^n\Bigr) \end{align*}$

と表せるとき，この右辺を$f$の$\alpha$中心のLaurent展開という．また，$f$が$\alpha$中心のLaurent展開で表せるとき，$f$は$\alpha$でLaurent展開可能であるという．

いつ複素関数がLaurent展開可能かについては次の定理が重要で，後でこの定理を証明します．

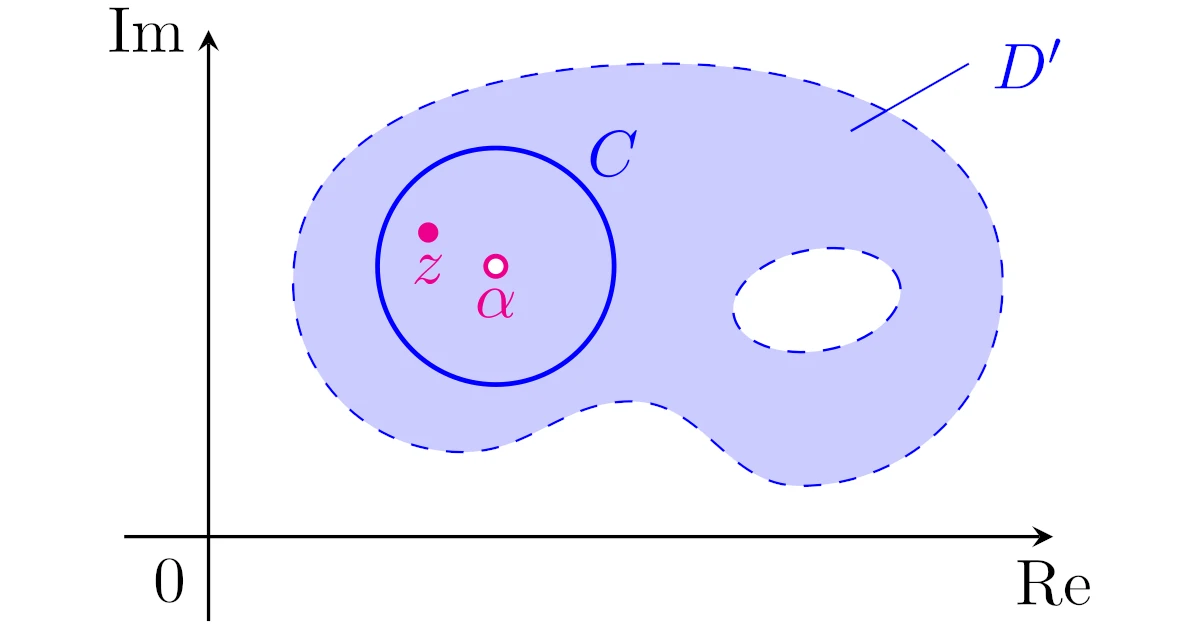
[ローラン展開可能性]　領域$D$から$\alpha\in D$を除いた領域$D’$上の正則関数$f$を考え，周および内部が$D$に含まれる$\alpha$中心の円周$C$をとる．このとき，$f$は$C$の内部から$\alpha$を除いた領域で

$\begin{align*} f(z)=&\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots \end{align*}$

と表せる．すなわち，$\alpha$中心でローラン展開可能である．

上で説明した[Taylor展開可能性]と比較すると，点$\alpha$で微分可能かどうかだけで

$\alpha$の近くで複素微分可能　→　$\alpha$でTaylor展開可能
$\alpha$を除く$\alpha$の近くで複素微分可能　→　$\alpha$でLaurent展開可能

という違いになります．

つまり，Laurent展開は$\alpha$で微分可能性が分からないときの展開で，$\alpha$で微分可能であることが分かれば$c_{-1}=c_{-2}=c_{-3}=\dots=0$となってTaylor展開可能であることになりますね．

留数

上の[ローラン展開]の定理において，係数$c_{k}$はのちに説明するように

$\begin{align*} c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta \end{align*}$

となります．このうち，$c_{-1}$に注目すると

$\begin{align*} c_{-1}=\frac{1}{2\pi i}\int_{C}f(\zeta)\,d\zeta \iff \int_{C}f(\zeta)\,d\zeta=2\pi i c_{-1} \end{align*}$

となっています．このように，この$c_{-1}$は複素積分に密接に関わるものとして以下のように定義されます．

[留数]　上のローラン展開の$c_{-1}$を$f$の$\alpha$における留数(residue)といい，$\mrm{Res}(f,\alpha)$や$\mrm{Res}_{\alpha}f$などと表す．

のちに説明するようにローラン展開は１通りしかないため，この留数は１つに定まります．

つまり，留数$\mrm{Res}(f,\alpha)$を$2\pi i$倍することで$\alpha$周りでの$f$の複素積分が求まるわけですね．

Laurent展開$f(z)=\dsum_{n=-\infty}^{\infty}c_n(z-\alpha)^n$に対して，

$\begin{align*} \int_{C}f(z)\,dz=2\pi ic_{-1} \end{align*}$

なので，$c_{-1}$は積分しても「留まる数」ということで留数と名付けられているわけですね．なお，英語の”residue”は「残り物」という意味です．

ローラン展開可能性と一意性の証明

最後に先ほど述べた[ローラン展開可能性]の定理と，ローラン展開の一意性を証明しましょう．

ローラン展開可能性の証明

正則関数のTaylor展開もそうでしたが，Laurent展開も次のCauchyの積分公式を用いて導かれます．

[Cauchyの積分公式]　領域$D$上で正則な複素関数$f$を考える．任意の$z\in D$に対して，$z$を内部に含む$D$内の閉曲線$C_z$を考え，$C_z$の内部でも$f$が正則なら

$\begin{align*} f(z)=\frac{1}{2\pi i}\int_{C_z}\frac{f(\zeta)}{\zeta-z}\,d\zeta \end{align*}$

が成り立つ．ただし，$C_z$の向きは正方向とする．

【前々回の記事：複素解析５｜縁の下の力持ち[コーシーの積分公式]を解説】

この記事ではCauchyの積分公式を直感的に理解する考え方を説明しています．

[ローラン展開可能性(再掲)]　領域$D$から$\alpha\in D$を除いた領域$D’$上の正則関数$f$を考え，周および内部が$D$に含まれる$\alpha$中心の円周$C$をとる．このとき，$f$は$C$の内部から$\alpha$を除いた領域で

$\begin{align*} f(z)=\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots \end{align*}$

と表せる．すなわち，$\alpha$中心でローラン展開可能である．

証明を表示

$C$の内部の任意の点$z$をとる．また，$C_{z}$, $C’$はそれぞれ$C$の内部の$z$, $\alpha$中心の円周で，互いに外部にあるようにとる．

$f$は点$\alpha$で微分不可能であり，$\frac{1}{\zeta-z}$が点$z$で微分不可能であることに注意すると，$\frac{f(\zeta)}{\zeta-z}$は２点$\alpha$, $z$で微分不可能だから，Cauchyの積分定理より

$\begin{align*} &\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta =\int_{C_{z}}\frac{f(\zeta)}{\zeta-z}\,d\zeta+\int_{C'}\frac{f(\zeta)}{\zeta-z}\,d\zeta \end{align*}$

が成り立つ．ただし，$C$, $C_z$, $C’$はいずれも正の向きがついているとする．

【複素解析４｜超強力な[コーシーの積分定理]とその使い方】

Cauchyの積分定理は「領域$D$上の正則関数$f$を，周も内部も$D$に含まれる閉曲線$C$上で積分すると０である」という非常に美しい定理です．その応用として「正則領域内で閉積分曲線を連続的に変形させても複素積分の値が変化しない」が成り立ちます．

また，Cauchyの積分公式より

$\begin{align*} f(z)=\frac{1}{2\pi i}\int_{C_{z}}\frac{f(\zeta)}{\zeta-z}\,d\zeta\quad\dots(**) \end{align*}$

が成り立つので，これらを併せて

$\begin{align*} f(z)&=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta-\frac{1}{2\pi i}\int_{C'}\frac{f(\zeta)}{\zeta-z}\,d\zeta \\&=:I+I\!I \end{align*}$

が成り立つ．前回の記事の[Taylor展開可能性]の証明では$I$のみで

$\begin{align*} &I=a_{0}+a_{1}(z-\alpha)+a_{2}(z-\alpha)^{2}+\dots, \\&c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta \end{align*}$

とTaylor展開できたから，あとは$I\!I$を

$\begin{align*} I\!I=\frac{c_{-1}}{z-\alpha}+\frac{c_{-2}}{(z-\alpha)^{2}}+\dots \end{align*}$

と展開できることを示せば良い．

$I\!I$の積分の中身は

$\begin{align*} \frac{f(\zeta)}{\zeta-z} =&\frac{f(\zeta)}{z-\alpha}\cdot\frac{1}{\frac{\zeta-z}{z-\alpha}} \\=&-\frac{f(\zeta)}{z-\alpha}\cdot\frac{1}{1-\frac{\zeta-\alpha}{z-\alpha}} \\=&-\frac{f(\zeta)}{z-\alpha}\sum_{k=1}^{\infty}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1} \end{align*}$

ただし，$|\zeta-\alpha|<|z-\alpha|$より$|\frac{\zeta-\alpha}{z-\alpha}|<1$だから，$\frac{1}{1-\frac{\zeta-\alpha}{z-\alpha}}$は初項１，公比$\frac{\zeta-\alpha}{z-\alpha}$の等比級数であることを用いた．よって，

$\begin{align*} I\!I=&-\frac{1}{2\pi i}\int_{C'}\frac{f(\zeta)}{z-\alpha}\sum_{k=1}^{\infty}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1}\,d\zeta\quad\dots(*) \end{align*}$

が成り立つ．

ここで，$(*)$の極限(級数)と積分の順序交換をするため，$\int_{C}$の中の$C$上の複素関数を

$\begin{align*} g_n(\zeta):=\sum_{k=1}^{n}\frac{f(\zeta)}{z-\alpha}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1} \end{align*}$

と定め，関数列$\{g_n\}_{n=0}^{\infty}$が$n\to\infty$で$C’$上一様収束することをWeierstrass(ワイエルシュトラス)のM判定法を用いて示す．

$C’$の半径を$R$とする．円周$C’$は有界閉集合(コンパクト集合)なので，$C’$上で連続な$f$は最大値$M$をもつから，任意の$\zeta\in C’$に対して

$\begin{align*} \abs{\frac{f(\zeta)}{z-\alpha}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1}} \le\frac{M}{|z-\alpha|}\bra{\frac{R}{|z-\alpha|}}^{k-1} \end{align*}$

が成り立つ．$\frac{R}{|z-\alpha|}<1$だから級数$\sum_{k=0}^{\infty}\frac{M}{|z-\alpha|}\bra{\frac{R}{|z-\alpha|}}^{k-1}$は収束するので，WeierstrassのM判定法より関数列$\{g_n\}$は一様収束する．

よって，$(*)$で極限(級数)と積分の順序交換ができて

$\begin{align*} I\!I =&-\frac{1}{2\pi i}\sum_{k=1}^{\infty}\frac{1}{(z-\alpha)^k}\int_{C'}f(\zeta)(\zeta-\alpha)^{k-1}\,d\zeta \\=&\frac{c_{-1}}{z-\alpha}+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-3}}{(z-\alpha)^{3}}+\dots \end{align*}$

を得る．ただし，$c_{-k}=\dfrac{1}{2\pi i}\dint_{C’}f(\zeta)(\zeta-\alpha)^{k-1}\,d\zeta$ ($k=1,2,\dots$)とおいた．

この係数$c_k$は$z$によらないから示された．

なお，最後の$c_{-k}=\dfrac{1}{2\pi i}\dint_{C}f(\zeta)(\zeta-\alpha)^{k-1}\,d\zeta$は$-k$を$k$に換え，また被積分関数$\dfrac{f(\zeta)}{(\zeta-\alpha)^{k+1}}$が正則な領域内で積分経路$C’$は$C$に変形できるから

$\begin{align*} c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta \end{align*}$

となり，$I$の$k\ge0$のときも$I\!I$の$k<0$のときも同じ形であることが分かりますね．

ローラン展開の一意性

最後にローラン展開の一意性，つまり係数$c_k$が１通りしかないことを示します．

[Laurent展開の一意性]　領域$D$から$\alpha\in D$を除いた領域$D’$上の正則関数$f$を考え，周および内部が$D$に含まれる$\alpha$中心の円周$C$をとる．このとき，$f$は$C$の内部から$\alpha$を除いた領域でのローラン展開は一意である．すなわち，

$\begin{align*} f(z)=\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^n=\sum_{n=-\infty}^{\infty}d_n(z-\alpha)^n \end{align*}$

と表せたとすると，$c_n=d_n$ ($n\in\Z$)が成り立つ．

証明を表示

任意に円周$C$の半径を$R$とし，任意に$k\in\Z$をとる．また，任意に$r\in(0,R)$をとる．

$C$上の点で整級数

$\begin{align*} \sum_{n=0}^{\infty}c_n(z-\alpha)^{n-k-1},\quad \sum_{n=0}^{\infty}d_n(z-\alpha)^{n-k-1} \end{align*}$

が収束するから，微分積分学の整級数と同様に中心$\alpha$，半径$r$の円内部$A_2=\set{z\in\C}{|z-\alpha|<r}$でいずれの整級数も一様収束する．

同様に，

$\begin{align*} \sum_{n=-\infty}^{-1}c_n(z-\alpha)^{n-k-1},\quad \sum_{n=-\infty}^{-1}d_n(z-\alpha)^{n-k-1} \end{align*}$

は中心$\alpha$，半径$r$の円外部$A_2=\set{z\in\C}{r<|z-\alpha|}$で一様収束する．

$r\in(0,R)$は任意だったから，領域$A_1\cap A_2=\set{z\in\C}{0<|z-\alpha|<R}$で

$\begin{align*} \sum_{n=-\infty}^{\infty}c_n(z-\alpha)^{n-k-1},\quad \sum_{n=-\infty}^{\infty}d_n(z-\alpha)^{n-k-1} \end{align*}$

はいずれも一様収束する．

よって，$\dsum_{n=-\infty}^{\infty}c_n(z-\alpha)^n=\dsum_{n=-\infty}^{\infty}d_n(z-\alpha)^n$の両辺に$(z-\alpha)^{-k-1}$をかけて，両辺を$C’$上で積分すると

$\begin{align*} &\int_{C_r}\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^{n-k-1}\,dz=\int_{C_r}\sum_{n=-\infty}^{\infty}d_n(z-\alpha)^{n-k-1}\,dz \\\iff&\sum_{n=-\infty}^{\infty}\int_{C_r}c_n(z-\alpha)^{n-k-1}\,dz=\sum_{n=-\infty}^{\infty}\int_{C_r}d_n(z-\alpha)^{n-k-1}\,dz \end{align*}$

が成り立つ．ただし，$C_r$は中心$\alpha$，半径$r$の円周である．計算により

$\begin{align*} \int_{C_r}c_n(z-\alpha)^{n-k-1}\,dz =\begin{cases}0&(n\neq k)\\2\pi i&(n\neq k)\end{cases} \end{align*}$

だから，$2\pi ic_{k}=2\pi id_{k}\iff c_{k}=d_{k}$となってLaurent展開の一意性が成り立つ．

最後の複素積分$\dint_{C_r}c_n(z-\alpha)^{n-k-1}\,dz$の計算については以前の記事で実際に計算しているので，詳しくはそちらを参照してください．

【複素解析３｜複素平面で積分しよう！複素積分の具体例も紹介】

複素積分を直接計算する方法としては，積分経路上の積分変数$z$を実変数$t$で表して実数のリーマン積分$t$に持ち込む方法です．

また，Laurent展開が一意であることから

とくにTaylor展開も一意
留数も一意

であることが分かりますね．

留数定理

次の記事では，この一連の記事の目標である留数定理を説明し，次の問題に応用します．

次の広義積分を計算せよ．

$\begin{align*} \int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx. \end{align*}$

留数定理を用いるには龍数を求める必要があるためLaurent展開をする必要があります．

そのため，具体的にLaurent展開を求める方法を知りたい方は次の記事を参照してください．

「複素解析」の一連の記事はこちら

【複素解析１｜複素関数とは何か？図示の仕方も説明】
【複素解析２｜正則関数は超重要！複素関数の微分の考え方】
【複素解析３｜複素平面で積分しよう！複素積分の具体例も紹介】
【複素解析４｜超強力な[コーシーの積分定理]とその使い方】
【複素解析５｜縁の下の力持ち[コーシーの積分公式]を解説】
【複素解析６｜１回でも微分できれば[テイラー展開]できる！】
【複素解析７｜[ローラン展開]はテイラー展開の進化形！】
【複素解析８｜[留数定理]を使って広義積分を計算する方法】←次の記事

参考文献

[新装版]複素関数論の要諦

[堀川穎二著/日本評論社]

本書は著者が実際に大学の授業で行った授業をもとに書かれており，説明も丁寧で分かりやすいです．

まえがきに「大学１年生の微分・積分の概要を理解している人を想定している」と書いてあるように，初めて複素解析を学ぶ人が基礎を理解するにはちょうど良いレベル感で書かれています．

式変形も丁寧になされており行間が少ないので，これは初学者にとって嬉しいポイントですね．

内容も留数定理，偏角の原理までフォローされているので，ひとまず複素解析が実数の定積分への応用まで学ぶことができます．

また，巻末に実際に授業を行った際のアンケートなどが載っており，学生から見て本書の内容(の授業)がどのようであったかを感じられるのは本書の面白いところです．

Amazon 楽天市場