ハーディの不等式はソボレフの不等式のように,ソボレフ空間の埋め込みを示す次の不等式のことをいいます:
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^q}\,dx
\lesssim\bra{\int_{\R^d}|f(x)|^p\,dx}^{\frac{p-q}{p}}\bra{\int_{\R^d}|\nabla{f}(x)|\,dx}^{\frac{q}{p}}\end{align*}
ハーディの不等式は偏微分方程式論などで空間の重みが付いた積分を評価する際に用いられ,通常のソボレフの不等式と同様に重要な不等式となっています.
なお,ハーディの不等式は極座標変換,部分積分,ヘルダーの不等式を用いれば,(通常のソボレフの不等式と比べて)比較的容易に示すことができます.
この記事では
- ハーディの不等式の主張
- ハーディの不等式の証明
を順に証明します.
ハーディの不等式
次の不等式をハーディの不等式(Hardy’s inequality)といいます.
$d\ge2$は次元とし,$p,q\in\R$は$1\le p<\infty$, $q<d$, $0\le q\le p$を満たすとする.このとき,任意の$f\in W^{1,p}(\R^d)$に対して,
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^q}\,dx
\le\bra{\frac{p}{d-q}}^{q}\|f\|_{p}^{p-q}\|\nabla{f}\|_{p}^{q}\end{align*}
が成り立つ.ただし,$W^{1,p}(\R^d)$は非斉次ソボレフ空間であり,$\|\cdot\|_p$は$L^p(\R^d)$ノルムである.
ハーディの不等式における定数$\bra{\frac{p}{d-q}}^{q}$は最良であることも証明できます.
よく知られているように$0<q<d$なら$\frac{1}{|x|^q}$は$|x|\to\infty$で減衰が弱く可積分ではありません.
実際,極座標変換$x=r\omega$ ($r=|x|$, $\omega\in\mathbb{S}^{d-1}$)に関してヤコビ行列式の絶対値が$r^{d-1}$で上から評価できることから
\begin{align*}\int_{\R^d}\frac{1}{|x|^q}\,dx
&\le\int_{\mathbb{S}^{d-1}}\int_{0}^{\infty}\frac{1}{r^q}r^{d-1}\,dr\,d\omega
\\&=|\mathbb{S}^{d-1}|\brc{\frac{r^{d-q}}{d-q}}_{0}^{\infty}\end{align*}
ですから,$q<d$なら$r\to\infty$で可積分ではありませんね.
つまり,ハーディの不等式は「$f\in W^{1,p}(\R^d)$に対して,$|f|^p$は$\frac{1}{|x|^q}$をかけても可積分であるくらいの特異性・減衰をもつ」という意味になっているわけですね.
ハーディの不等式の証明
補題を示してから,ハーディの不等式を示します.
補題
$d\ge2$は次元とし,$p\in\R$は$1\le p<\infty$を満たすとする.このとき,任意の$f\in \dot{W}^{1,p}(\R^d)$に対して,
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^p}\,dx
\le\bra{\frac{p}{d-p}}^{p}\|\nabla{f}\|_{p}^{p}\end{align*}
が成り立つ.ただし,$\dot{W}^{1,p}(\R^d)$は斉次ソボレフ空間であり,$\|\cdot\|_p$は$L^p(\R^d)$ノルムである.
この補題の不等式をハーディの不等式ということもあります.
$f\in C^{\infty}_{0}(\R^d)$の場合を示す.極座標変換$x=r\omega$ ($r=|x|$, $\omega\in\mathbb{S}^{d-1}$)を用いると
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^p}\,dx
\le&\int_{\mathbb{S}^{d-1}}\int_{0}^{\infty}\frac{|f(r\omega)|^p}{r^p}\cdot r^{d-1}\,dr\,d\omega
\\=&\int_{\mathbb{S}^{d-1}}\int_{0}^{\infty}|f(r\omega)|^pr^{d-p-1}\,dr\,d\omega\end{align*}
である.$r^{d-q-1}=\pd{}{r}\bra{\frac{r^{d-q}}{d-q}}$だから,$r$について部分積分を用いると
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^p}\,dx
\le\frac{1}{d-q}\int_{\mathbb{S}^{d-1}}\int_{0}^{\infty}\pd{}{r}\bra{|f(r\omega)|^p}r^{d-p}\,dr\,d\omega\end{align*}
である.一般に$\pd{g}{r}(x)=\frac{x}{r}\cdot\nabla{g}(x)$だから,
\begin{align*}\pd{}{r}\bra{|f(r\omega)|^p}
=&\frac{x}{r}\cdot\nabla\bra{|f(x)|^p}
\\=&\frac{x}{r}\cdot\bra{p|f(x)|^{p-1}\nabla{f}(x)}
\\=&p|f(x)|^{p-1}\pd{f}{r}(x)\end{align*}
であり,極座標変換を元に戻して
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^p}\,dx
\le&\frac{1}{d-p}\int_{\mathbb{S}^{d-1}}\int_{0}^{\infty}p|f(x)|^{p-1}\pd{f}{r}(x)r^{d-p}\,dr\,d\omega
\\=&\frac{p}{d-p}\int_{\R^d}\frac{|f(x)|^{p-1}}{|x|^{p-1}}\pd{f}{r}(x)\,dx\end{align*}
を得る.よって,$1=\frac{p-1}{p}+\frac{1}{p}$に関するヘルダーの不等式より
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^p}\,dx
\le&\frac{p}{d-p}\bra{\int_{\R^d}\frac{|f(x)|^{p}}{|x|^{p}}\,dx}^{\frac{p-1}{p}}\bra{\int_{\R^d}\abs{\pd{f}{r}(x)}^{p}\,dx}^{1/p}\end{align*}
となる.両辺を$\bigl(\int_{\R^d}\bigl|\frac{f(x)}{x}\bigr|^{p}\,dx\bigl)^{\frac{p-1}{p}}$で割って$|\pd{f}{r}|=|\nabla{f}|$を用いると,
\begin{align*}&\bra{\int_{\R^d}\frac{|f(x)|^p}{|x|^p}\,dx}^{1/p}
\le\frac{p}{d-p}\bra{\int_{\R^d}|\nabla{f}(x)|^p\,dx}^{1/p}\end{align*}
が従う.$\dot{W}^{1,p}(\R^d)$における$C^{\infty}_{0}(\R^d)$の稠密性と併せて,$f\in \dot{W}^{1,p}(\R^d)$にも成り立つことが分かる.
ハーディの不等式の証明
この補題を$|f|^{p/q}$に適用すれば,次のように直ちにハーディの不等式が従います.
(再掲)$d\ge2$は次元とし,$p,q\in\R$は$1\le p<\infty$, $q<d$, $0\le q\le p$を満たすとする.このとき,任意の$f\in W^{1,p}(\R^d)$に対して,
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^q}\,dx
\le\bra{\frac{p}{d-q}}^{q}\|f\|_{p}^{p-q}\|\nabla{f}\|_{p}^{q}\end{align*}
が成り立つ.ただし,$W^{1,p}(\R^d)$は非斉次ソボレフ空間であり,$\|\cdot\|_p$は$L^p(\R^d)$ノルムである.
$p=q$のとき,定理は補題そのものなので示されている.
$q<p$のとき,$f\in W^{1,p}(\R^d)$に対して$g=|f|^{p/q}$とおく.このとき,$g\in\dot{W}^{1,q}(\R^d)$だから補題を適用できて
\begin{align*}&\int_{\R^d}\frac{|g(x)|^q}{|x|^q}\,dx
\le\bra{\frac{q}{d-q}}^{q}\|\nabla{g}\|_{q}^{q}
\\\iff&\int_{\R^d}\frac{|f(x)|^p}{|x|^q}\,dx
\le\bra{\frac{q}{d-q}}^{q}\|\nabla{|f|^{p/q}}\|_{q}^{q}\end{align*}
が成り立つ.また,$\frac{1}{q}=\frac{p-q}{pq}+\frac{1}{p}$に関するヘルダーの不等式より
\begin{align*}\|\nabla{|f|^{p/q}}\|_{q}
=&\nor{\frac{p}{q}|f|^{\frac{p}{q}-1}\nabla{f}}_{q}
\\\le&\frac{p}{q}\|f\|_{p}^{\frac{p-q}{q}}\|\nabla{f}\|_{p}\end{align*}
だから,ハーディの不等式
\begin{align*}\int_{\R^d}\frac{|f(x)|^p}{|x|^q}\,dx
\le\bra{\frac{p}{d-q}}^{q}\|f\|_{p}^{p-q}\|\nabla{f}\|_{p}^q\end{align*}
が従う.

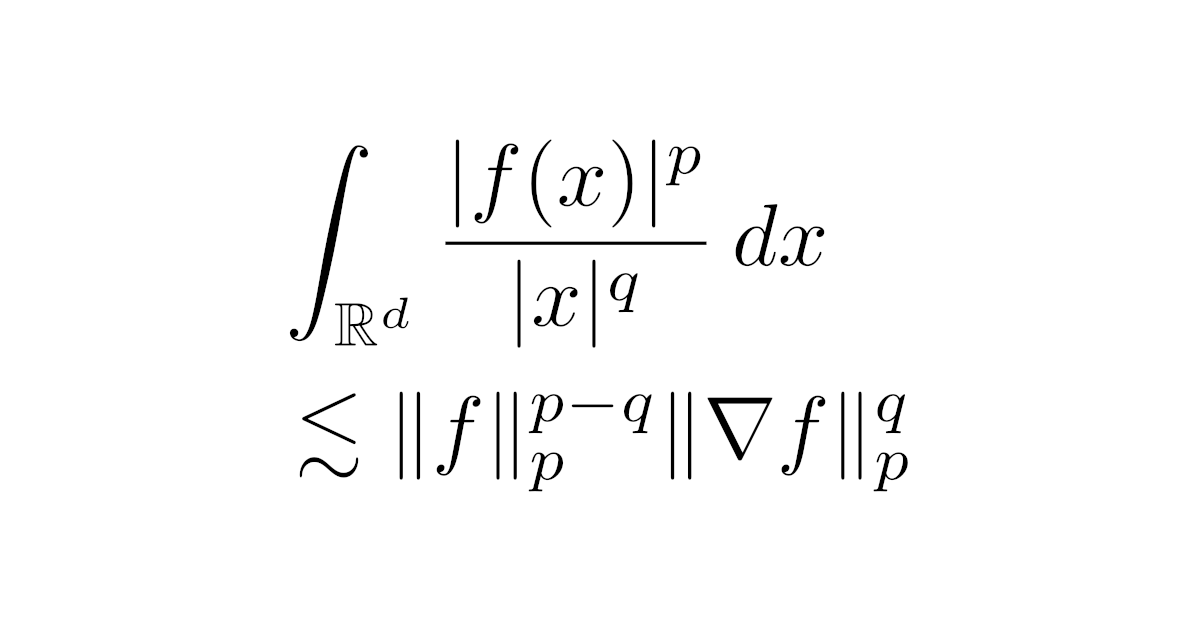
コメント