ルベーグ空間（Lᵖ空間）の共役空間｜リースの定理を添えて

関数空間
2021.03.23
関数空間

体$\R$上の有限次元線形空間$V$に対して，線形写像$V\to\R$全部の集合は$V$の双対空間とよばれ，$V^*$と表されることは線形代数学で学びますね：

$V^{*}=\set{f:V\to\R}{\text{$f$は線形写像}}$．

$V$が無限次元ノルム空間の場合には，線形写像$V\to\R$のうち（汎関数として）有界なもの全部の空間を共役空間と呼び，やはり$V^*$と表します．

無限次元の線形空間を扱う分野として関数解析学がありますが，関数解析学ではこの共役空間が重要な役割を果たします．

さて，$p\in[1,\infty)$に対して，$p$乗ルベーグ可積分関数の集合は$L^p$と表され，$L^p$ノルム$\|\cdot\|_{L^p}$によってノルム空間となります．

$L^p$は正確には$p$乗ルベーグ可積分関数の集合で，ほとんど至るところで等しい関数を同一視してできる集合です．

実は$\frac{1}{p}+\frac{1}{q}=1$で$q$を定めるとき，$L^p$の共役空間$(L^p)^*$は$L^q$と同一視できることが知られています．

この記事では，（証明まではしませんが）この同型$(L^p)^*\cong L^q$の考え方をリース (Riesz)の表現定理と併せて説明します．

なお，複素数体$\C$上の線形空間に対しても同様に成り立ちますが，本記事での線形空間は全て実数体$\R$上の線形空間とします．

共役空間

まずは一般の共役空間を定義しましょう．

線形汎関数の定義

先に共役空間の元である有界線形汎関数を定義しましょう．

線形空間$V$から$\R$への写像を$V$上の汎関数 (functional)という．とくに汎関数が線形のときには線形汎関数 (linear functional)という．

ノルム空間$(V,\|\cdot\|_V)$を考える．$V$上の線形汎関数$f$が

   \begin{align*}\|f\|_{*}:=\sup_{u\in V\setminus\{0\}}\frac{|f(u)|}{\|u\|_V}<\infty\end{align*}

を満たすとき，$f$は有界 (bounded)であるという．

$V$上の線形汎関数$f$と$u\in V$に対して

  • $\|u\|_{V}$は$u$の$V$での長さ
  • $|f(u)|$は$f(u)$の$\R$での長さ

ですから，$\frac{|f(u)|}{\|u\|_V}$は線形汎関数$f:V\to\R$を施す前の長さに対する後の長さの比ということになります．

$u\in V$を自由に動かしたときの上限が$\|f\|_{*}$ですから，線形汎関数$f$が有界であるとは$f$を施す前後の長さの比が有界であることということができますね．

ノルム空間$V$が有限次元なら，任意の線形汎関数は有界となることが証明できます．よって，有界でない線形汎関数が存在するのは，無限次元の場合に限ります．

共役空間の定義

それでは共役空間を定義しましょう．

ノルム空間$(V,\|\cdot\|_V)$上の有界線形汎関数全部の集合を$V^*$と表す．

このとき，$\|\cdot\|_{*}$は$V^*$のノルムとなり，こうしてできるノルム空間$(V^*,\|\cdot\|_{*})$を$V$の共役空間 (conjugate space)または双対空間 (dual space)という．

以降，この記事では$V^*$上のノルム$\|\cdot\|_{*}$を$\|\cdot\|_{V^{*}}$と表すことにします．

リースの表現定理

次にリース(Riesz)の表現定理とよばれる内積空間の$\|\cdot\|_{V^*}$ノルムに関する定理を説明します．

重要な命題

リースの表現定理のベースとなるのは次の命題です．

内積空間$(V,\anb{\cdot,\cdot}_{V})$を考える．$v\in V$に対して$f_{v}:V\to\R$を

   \begin{align*}f_{v}(u):=\anb{u,v}_{V}\end{align*}

で定める．このとき，$f_{v}\in V^{*}$と$\|f_{v}\|_{V^{*}}=\|v\|_{V}$が成り立つ．

例えば，標準内積を備えた$\R^3$で$v:=\bmat{1\\2\\3}$とすると，$f_v$は

   \begin{align*}&f_v\bra{\bmat{0\\1\\0}}=\anb{\bmat{0\\1\\0},\bmat{1\\2\\3}}=2, \\&f_v\bra{\bmat{2\\0\\-1}}=\anb{\bmat{2\\0\\-1},\bmat{1\\2\\3}}=-1\end{align*}

という汎関数ですね．

内積の第１成分に関する線形性から$f\in V^{*}$が成り立つ．

任意の$u\in V\setminus\{0\}$に対して，コーシー-シュワルツ(Cauchy-Schwarz)の不等式より

   \begin{align*}|f_{v}(u)|=|\anb{u,v}_{V}|\le\|u\|_{V}\|v\|_{V}\end{align*}

なので，両辺を$\|u\|_{V}$で割って$u\in V\setminus\{0\}$で上限をとれば$\|f_{v}\|_{V*}\le\|v\|_{V}$が成り立つ．

一方，

   \begin{align*}|f_{v}(v)|=|\anb{v,v}_{V}|=\|v\|_{V}^{2}\end{align*}

なので，両辺を$\|v\|_{V}$で割って

   \begin{align*}\|f_{v}\|_{V^{*}}\ge\frac{|f_{v}(v)|}{\|v\|_{V}}=\|v\|_{V}\end{align*}

が成り立つ．

リース表現

いまの命題は内積から線形汎関数を作りましたが，逆に$V$がヒルベルト空間（完備な内積空間）なら任意の線形汎関数は内積を使って表せることが証明できます．

すなわち，次の定理が成り立ち，この定理をリースの表現定理といいます．

[リースの表現定理] 任意の$f\in V^{*}$に対して，ある$v\in V$が一意に存在して

   \begin{align*}f=f_{v}=\anb{\cdot,v}_{V}\end{align*}

かつ$\|f\|_{V^*}=\|v\|_V$が成り立つ．

このように$f\in V^{*}$の内積で表すことをリース表現といいます．

このリースの表現定理から次のようにヒルベルト空間は自分の共役空間と同型であることが分かりますね．

ヒルベルト空間$V$に対して，写像

   \begin{align*}\tau:V\to V^{*};v\mapsto f_{v}\end{align*}

は同型である：$\tau:V\stackrel{\sim}{\to}V^{*}$．

$\tau$は内積の性質から単射，リースの表現定理から全射かつリースの表現定理から等長である．

よって，$\tau$はユニタリ作用素だから，$V\cong V^{*}$である．

ルベーグ空間（$L^p$空間）の共役空間

最後にルベーグ空間（$L^p$空間）を定義し，この共役空間について説明します．

ルベーグ空間の定義

$\Omega\subset\R^{d}$を可測集合とします．

$\Omega$上のルベーグ可測関数$f$に対して，

   \begin{align*}&\|f\|_{L^{p}}:=\bra{\int_{\Omega}|f(x)|^{p}}^{1/p}, \\&\|f\|_{L^{\infty}}:=\inf\set{\lambda>0}{|f|\le\lambda\ \mrm{a.e.}}\end{align*}

とおく．$p\in[1,\infty)$に対して，$\Omega$上で$p$乗ルベーグ可積分関数の集合を$L^{p}(\Omega)$と表す：

$L^{p}(\Omega)=\set{f:\Omega\to\R:\text{可測}}{\|f\|_{L^{p}}<\infty}$．

また，$\Omega$上で本質的有界なルベーグ可測関数の集合を$L^{\infty}(\Omega)$と表す：

$L^{\infty}(\Omega)=\set{f:\Omega\to\R:\text{可測}}{\|f\|_{L^{\infty}}<\infty}$．

このとき，任意の$p\in[1,\infty]$に対して，$\|\cdot\|_{L^p}$は$L^p$のノルムとなり，この空間をルベーグ (Lebesgue)空間という．

正確には$L^p$は上記の集合をさらにほとんど至るところで等しい関数たちを同一視してできる商集合です．

ルベーグ空間$L^p$はバナッハ空間（完備なノルム空間）となります．とくに$p=2$の場合は中線定理を満たしヒルベルト空間となり，内積は

   \begin{align*}\anb{u,v}_{L^{2}}=\int_{\Omega}u(x)v(x)\,dx\end{align*}

となります．

ヘルダーの不等式

リースの表現定理のところで考えたように

   \begin{align*}f_v:L^2\to\R;u\mapsto\anb{u,v}_{L^2}\end{align*}

で線形汎関数を定めると，コーシー-シュワルツの不等式から

   \begin{align*}|f_{v}(u)|=\abs{\int_{\Omega}u(x)v(x)\,dx}\le\|u\|_{L^{2}}\|v\|_{L^{2}}\end{align*}

が成り立ちます．

コーシー-シュワルツの不等式は$L^2$上での不等式でしたが，$p\neq2$の場合の$L^p$上への一般化である次のヘルダー (Hölder)の不等式があります．

[ヘルダーの不等式] $p\in[1,\infty)$に対して$\frac{1}{p}+\frac{1}{q}=1$で$q\in(1,\infty]$を定める．このとき，$u\in L^p$, $v\in L^q$に対して，$uv\in L^1$となり，次の不等式が成り立つ：

   \begin{align*}\abs{\int_{\Omega}u(x)v(x)\,dx}\le\|u\|_{L^{p}}\|v\|_{L^{q}}.\end{align*}

$p=1$のときは$q=\infty$とします．

よって，$v\in L^q$に対して，$L^2$の場合と同様に線形汎関数

   \begin{align*}f_v:L^p(\Omega)\to\R;u\mapsto\int_{\Omega}u(x)v(x)\,dx\end{align*}

とすると，ヘルダーの不等式から$u\neq0$なら

   \begin{align*}|f_{v}(u)|\le\|u\|_{L^{p}}\|v\|_{L^{q}} \iff\|f\|_{(L^p)^{*}}\le\|v\|_{L^{q}}\end{align*}

が成り立ち，$f_v$は有界となります：$f_v\in(L^p)^{*}$．

共役空間$(L^p)^{*}$

実は逆向きの不等式$\|f\|_{(L^p)^{*}}\ge\|v\|_{L^{q}}$が成り立つことも証明することができ（証明略），したがって写像

   \begin{align*}\tau:L^q\to (L^p)^{*};v\mapsto f_{v}\end{align*}

は同型となります：$L^q\cong (L^p)^{*}$．

一般に$\frac{1}{p}+\frac{1}{q}=1$の関係にある$p,q\in(1,\infty]$をヘルダー共役といいますが，指数$p\in[1,\infty)$のルベーグ空間の共役空間は指数がヘルダー共役なルベーグ空間と同型になるわけですね．

そのため，$p\in(1,\infty)$に対して，$L^p$の共役空間の共役空間は

   \begin{align*}((L^p)^{*})^{*}=(L^q)^*=L^p\end{align*}

と元に戻りますね．

２回共役をとって元に戻る空間を回帰的共役空間といいます．任意の$p\in(1,\infty)$に対して$L^p$は回帰的です（$L^\infty$の共役空間は$L^1$とはならないことに注意）．

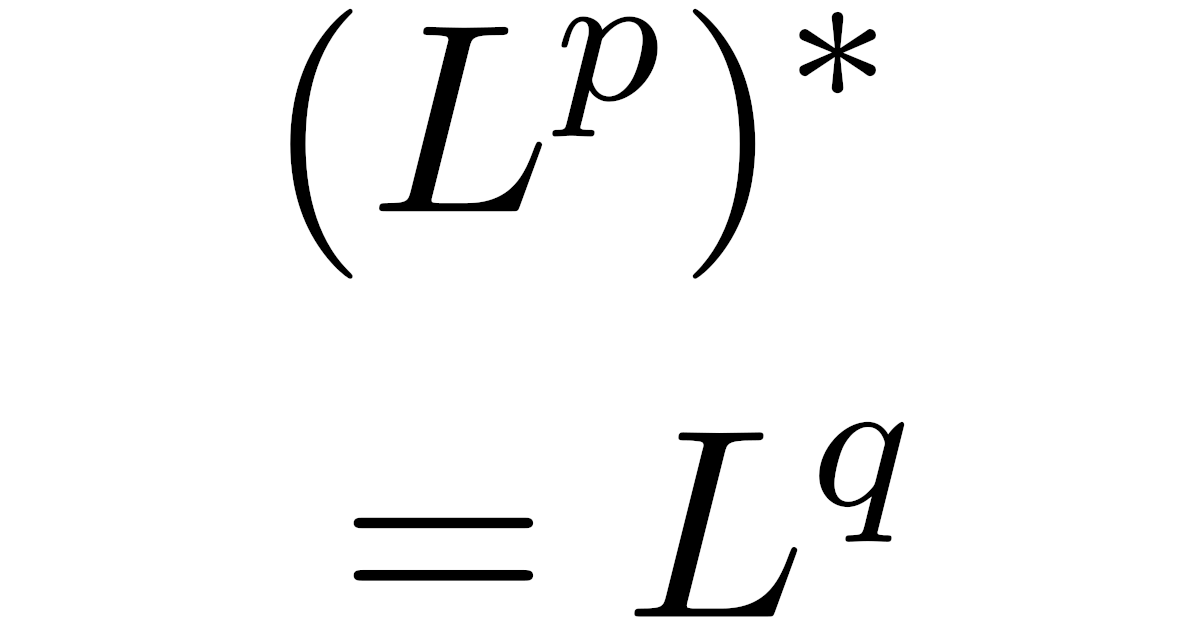
コメント