大学の微分積分学で学ぶリーマン積分は定義域を細かく分割して長方形近似によって面積を求める積分で，このことからリーマン積分は「縦切りの積分」ということができます．
一方，ルベーグ積分はリーマン積分とは対照的に値域に注目して分割する積分で，このことからルベーグ積分は「横切りの積分」と言われることもあります．
ルベーグ積分は定義までは少々道のりが長いものの，一度整備してしまえば非常に性質がよく扱い易い積分となっています．
さて，ルベーグ積分を考えるには「集合の『長さ』」が鍵となります．
例えば「区間$[0,1]$の長さ」はもちろん$1$ですが，それでは「区間$[0,1]$上の有理数の集合$\Q\cap[0,1]$の長さ」はどのように考えればよいでしょうか？
集合$\Q\cap[0,1]$は「まばら」な集合なので，我々がこれまで考えてきた「長さ」とは少し考え方を変える必要がありそうですね．
この記事では
- 外測度の定義
- 外測度の具体例
を順に解説します．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
外測度の定義
外測度とは集合の長さを「外側」から測るものと言うことができるため，そのように名前が付いています．
右半開区間$[a,b)$の長さを$b-a$と定める
外測度を定義するために，まずは区間の長さを定義しておきましょう．
$a,b\in\R$は$a<b$を満たすとする．このとき，右半開区間$[a,b)$の長さを
\begin{align*}|[b-a)|\end{align*}
と表し$b-a$と定める．
例えば，
\begin{align*}|[0,3)|=3-0=3,\quad
|[-3,1)|=1-(-3)=4\end{align*}
というわけですね．
「なぜ右半開区間を考えるのか」というと，例えば
\begin{align*}[0,1)\cup[1,3)=[0,3)\end{align*}
のように右半開区間であればピッタリと区間を繋げることができたりと扱いやすいことが理由です．
理論上は開区間でも，閉区間でも，左半開区間でも問題ないのですが，この一連の記事では右半開区間に対して長さを定義して話を進めます．
集合を右半開区間で覆って長さを考える
外測度の考え方を理解するために，まずは下図のような集合$A\subset\R$の長さを測る方法を考えましょう．
集合$A$は例えば下図のような右半開区間$I_1$, $I_2$によって覆うことができますね．
この$I_1$, $I_2$に対して，直感的には
(集合$A$の長さ)$\le|I_1|+|I_2|$
と言ってよさそうです．ただ，もっと「ゆとり」を小さく$A$を覆うこともできますね．
この$I’_1$, $I’_2$, $I’_3$に対しても，やはり
(集合$A$の長さ)$\le|I’_1|+|I’_2|+|I’_3|$
と言ってよさそうです．
これでもまだ$I’_2$には余裕がありますが，このように「ゆとり」を小さくしていけば，$A$を覆う区間たちの長さの和は集合$A$の「長さ」に近付いていくと言えそうですね．
外測度の定義
集合$A\subset\R$を右半開区間$I_1,I_2,I_3,\dots$で覆う方法は無数に考えられますが，
\begin{align*}\sum_{n=1}^{\infty}|I_n|=|I_1|+|I_2|+|I_3|+\dots\end{align*}
が小さくなるようにすると，これは集合$A$の「長さ」に近いと言えそうです．
この考え方で集合$A$の「長さ」を測るものを外測度といいます．
集合$A\subset\R$に対して，
$m^{*}(A)=\inf\set{\dsum_{n=1}^{\infty}|I_n|}{\begin{gathered}A\subset\textstyle\bigcup\limits_{n=1}^{\infty}I_n,\\\text{$I_n$は右半開区間}\end{gathered}}$
で定まる$m^{*}(A)$を$A$のルベーグ外測度または単に外測度という．
ただし，$A$を覆う右半開区間が有限個の場合，$\sum\limits_{n=1}^{\infty}|I_n|$は有限和とみなす．
実数の連続性公理より$\R$の部分集合の下限$\inf$は（$\pm\infty$を許して）必ず存在するので，$m^{*}$は任意の$A\subset\R$に対して定義できますね．
このことから，ルベーグ外測度$m^{*}$は$\R$の冪集合$\mathcal{P}(\R)$を定義域とする写像といえますね．
$\R$の部分集合全部の集合を冪集合といい，$\mathcal{P}(\R)$や$2^{\R}$などと表します．
また，ルベーグ外測度の定義の$\dsum_{n=1}^{\infty}|I_n|$は０以上なので，ルベーグ外測度は常に０以上ですね．
なお，「外測度」と呼ぶ理由は集合を右半開区間で「外側」から覆って「測る」ものだからですね．
外測度の具体例
いくつか簡単にルベーグ外測度が得られる具体例を考えてみましょう．
具体例１（空集合の外測度）
空集合$\emptyset$のルベーグ外測度が$0$であることを示せ．すなわち，$m^{*}(\emptyset)=0$を示せ．
任意に$\epsilon>0$をとる．空集合$\emptyset$は任意の集合の部分集合なので$\emptyset\subset[0,\epsilon)$だから，ルベーグ外測度の定義より
\begin{align*}m^{*}(\emptyset)\le|[0,\epsilon)|=\epsilon\end{align*}
が成り立つ．
$\epsilon$の任意性より$m^{*}(\emptyset)\le0$が成り立つから，もとより成り立つ$0\le m^{*}(\emptyset)$と併せて$m^{*}(\emptyset)=0$を得る．
具体例２（有限集合の外測度）
有限集合$\{a_1,a_2,\dots,a_n\}\subset\R$のルベーグ外測度が$0$であることを示せ．すなわち，$m^{*}(\{a_1,a_2,\dots,a_n\})=0$を示せ．
考え方は例１とほとんど同じです．
任意に$\epsilon>0$をとる．$I_k:=\left[a_k,a_k+\frac{\epsilon}{n}\right)$とおくと，
\begin{align*}\{a_1,a_2,\dots,a_n\}\subset\bigcup_{k=1}^{n}I_k\end{align*}
である．
よって，ルベーグ外測度の定義より
\begin{align*}m^{*}(\{a_1,a_2,\dots,a_n\})
&\le\sum_{k=1}^{n}\abs{\left[a_k,a_k+\frac{\epsilon}{n}\right)}
\\&=\sum_{k=1}^{n}\brb{\bra{a_k+\frac{\epsilon}{n}}-a_k}=\epsilon\end{align*}
が成り立つ．
$\epsilon$の任意性より$m^{*}(\{a_1,a_2,\dots,a_n\})\le0$が成り立つから，もとより成り立つ$0\le m^{*}(\{a_1,a_2,\dots,a_n\})$と併せて$m^{*}(\{a_1,a_2,\dots,a_n\})=0$を得る．
具体例３（可算無限集合の外測度）
可算無限集合$A\subset\R$のルベーグ外測度が$0$であることを示せ．すなわち，$m^{*}(A)=0$を示せ．
可算無限集合なので$A=\{a_1,a_2,\dots\}$と全ての元に番号をつけることができますね．
しかし，例２と同じように長さが一定の右半開区間で覆うのでは，区間の長さの和が正の無限大$\infty$に発散してうまくいきません．
このような場合は和が等比級数となるように，どんどん小さくなる右半開区間を設定するとうまくいきます．
任意に$\epsilon>0$をとる．$A=\{a_1,a_2,\dots\}$を可算無限集合とする．$I_n:=\left[a_n,a_n+\frac{\epsilon}{2^n}\right)$とおくと，
\begin{align*}A\subset\bigcup_{n=1}^{\infty}I_n\end{align*}
である．
よって，外測度の定義より
\begin{align*}m^{*}(A)\le\sum_{n=1}^{\infty}|I_n|=\sum_{n=1}^{\infty}\frac{\epsilon}{2^n}=\epsilon\end{align*}
が成り立つ．
$\epsilon$の任意性より$m^{*}(A)\le0$が成り立つから，もとより成り立つ$0\le m^{*}(\{a\})$と併せて$m^{*}(\{a\})=0$を得る．
等比級数$\sum\limits_{n=1}^{\infty}\frac{1}{2^n}=1$は当たり前にしておきたいですね．
例えば，整数全部の集合$\N$や有理数全部の集合$\Q$は可算無限集合なので
\begin{align*}m^{*}(\N)=0,\quad
m^{*}(\Q)=0\end{align*}
が従いますね．さらに，冒頭で問題提起した集合$\Q\cap[0,1]$も可算集合なので
\begin{align*}m^{*}(\Q\cap[0,1])=0\end{align*}
が成り立つことが分かりますね．
具体例４（区間の外測度）
右半開区間$I\subset\R$のルベーグ外測度が$|I|$であることを示せ．すなわち，$m^{*}(I)=|I|$を示せ．
直感的にはルベーグ外測度$m^{*}$が集合の「長さ」を測るものなので$|I|$となりそうです．
しかし，左辺の$I$の外測度$m^{*}(I)$の定義は「$I$を覆うあらゆる右半開区間の列$\{I_n\}$を考えたときの，$\sum\limits_{n=1}^{\infty}|I_n|$の集合の下限$\inf$」なので，右辺の区間の長さ$|I|$のような単純な定義ではありません．
そのため，これらが等しいことは直ちに成り立つわけではありませんが，このことを証明するのがこの問題ですね．
$I\subset I$が成り立つから，外測度の定義より$m^{*}(I)\le I$が成り立つ．
また，$I$の外測度$m^{*}(I)$の定義より，任意の$\epsilon>0$に対して，$I\subset\bigcup\limits_{n=1}^{\infty}$なる右半開区間の列$\{I_n\}$が存在し
\begin{align*}m^{*}(I)+\epsilon>\sum_{n=1}^{\infty}|I_n|\end{align*}
が成り立つ．
また，$I\subset\bigcup\limits_{n=1}^{\infty}$より$|I|\le\sum\limits_{n=1}^{\infty}|I_n|$が成り立つことと併せて
\begin{align*}m^{*}(I)+\epsilon>|I|\end{align*}
が成り立つから，$\epsilon$の任意性より$m^{*}(I)\ge|I|$を得る．よって，$m^{*}(I)=|I|$が従う．
証明中の「右半開区間$I\subset\bigcup_{n=1}^{\infty}$なら$|I|\le\sum_{n=1}^{\infty}|I_n|$が成り立つ」という部分は，直感的には捉え易いと思いますが本来は証明すべき箇所です．
しかし，この証明は少々厄介なので，この一連の記事では省略します．証明が知りたい方は例えば序盤に紹介した参考文献を参照してください．
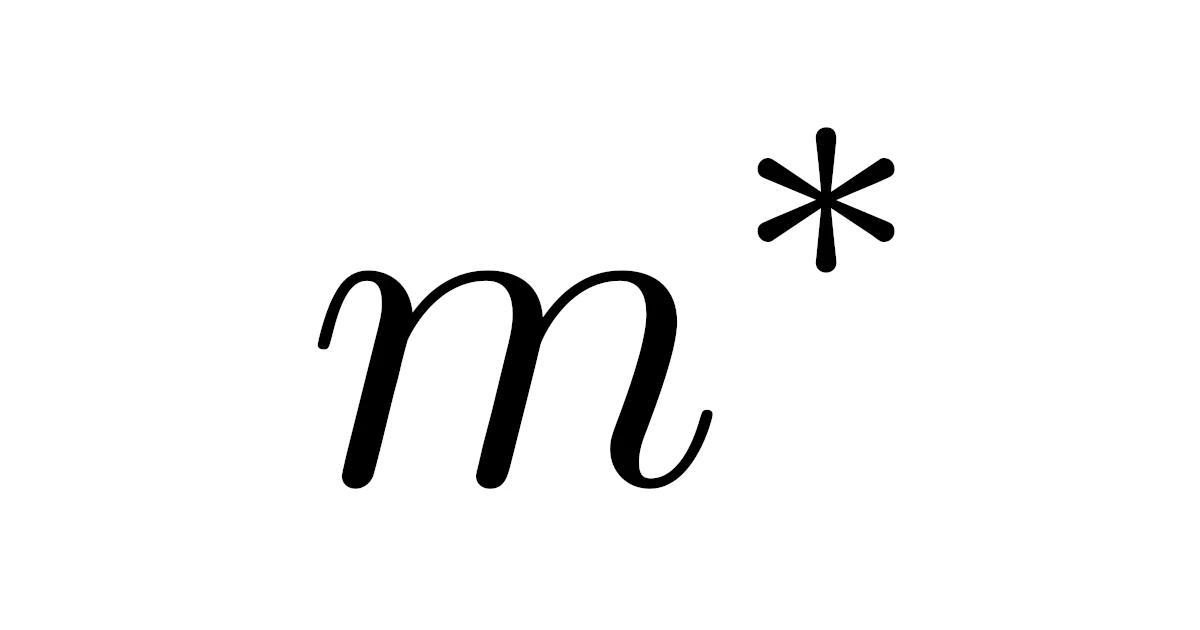
コメント