まずは，次の問題を考えましょう．
集合$A$, $B$をそれぞれ５以下の実数全部の集合，５未満の実数全部の集合とする：
\begin{align*}A=\set{x\in\R}{x\le5},\quad
B=\set{x\in\R}{x<5}.\end{align*}
このとき，集合$A$, $B$の最大値を答えよ．
数学では実数全部の集合を一般に$\R$で表します．そのため，たとえば「$a\in\R$に対して」は「実数$a$に対して」と同じ意味です．
最大値は集合に属していないといけないので，答えは「$A$の最大値は５であり，$B$の最大値は存在しない」となります．
このように５は集合$B$の最大値ではありませんが，$B$でも「５が最大っぽい値」になっているという気持ちはあります．
これら「最大値もしくは最大っぽい値」を上限といい，数学では頻繁に用いられます．同様に「最小値もしくは最小っぽい値」を下限といいます．
この記事では
- 上限と下限の定義
- 上限と下限の具体例
- 上限と下限の基本性質
- 上限と下限の存在性
を順に説明します．
「微分積分学の基本」の一連の記事
微分積分学の参考文献
以下は微分積分学に関するオススメの教科書です．
微分積分学（笠原晧司 著）
数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．
上限と下限
ここでは実数の集合の上限と下限の定義と具体例を説明します．
上限の定義
上限を定義するために必要な上界を定義しましょう．
集合$A\subset\R$を考える．$m\in\R$が$A$の上界 (upper bound)であるとは，任意の$a\in A$に対して$a\le m$を満たすことをいう．
また，$A$の上界が存在するとき，$A$は上に有界であるという．
つまり，集合$A$の任意の元以上となっている値$m$を集合$A$の上界というわけですね．
上限の具体例を考えましょう．
集合$A$, $B$を
\begin{align*}A=\set{x\in\R}{x\le5},\quad
B=\set{x\in\R}{x<5}\end{align*}
で定める．このとき，集合$A$, $B$の上界を全てを求めよ．
$A$の上界も$B$の上界も５以上の全ての実数である．
この例で大切なことは，５は集合$B$の最大値ではありませんが，集合$A$, $B$のどちらも５が上界の中で最小のものとなっている点です．
このことをもとに，次のように上限が定義されます．
$A$が上に有界であるとき，上界の最小値を$A$の上限（supremum）または最小上界といい$\sup{A}$と表す．一方，$A$が上に有界でないとき，$\sup{A}=\infty$と定める．
つまり，「『任意の$a\in A$に対して$a\le m$』を満たす$m\in\R$のうち最小のもの」を上限とよぶわけですね．
下限の定義
上限と同様に，下限も次のように定義されます．
$s\in\R$が$A\subset\R$の下界であるとは，任意の$a\in A$に対して$a\ge s$を満たすことをいい，$A$の下界が存在するとき$A$は下に有界であるという．
また，$A$が上に有界であるとき，$A$の下界の最大値を$A$の下限（infimum）または最大下界といい$\inf{A}$と表す．一方，$A$の下界が存在しないときは$\inf{A}=-\infty$と定める．
つまり，集合$A$の任意の元以下となっている値$s$を集合$A$の上界というわけですね．
上限と下限の具体例
具体例を考えてみましょう．
次の$\R$の部分集合それぞれの下限と上限を求めよ．
- $-2$以上３未満の実数上の区間$I$
- 正の整数全部の集合$\N$
- $0\le x\le 1$なる有理数$x$全部の集合$X$
(1) $\inf{I}=-2$, $\sup{I}=3$である．
(2) $\inf{\N}=1$, $\sup{I}=\infty$である．
(3) $\inf{X}=0$, $\sup{X}=1$である．
(3)は厳密にはアルキメデスの性質を必要としますが，この記事では省略します．
最大値が存在するときは最大値と上限は一致し，最小値が存在するときは最小値と下限は一致しますね．
上限と下限の基本性質
次に上限と下限に関する次の基本性質を示しておきましょう．
上に有界な$A\subset\R$に対して$\alpha=\sup{A}$とおく．このとき，任意の$\epsilon>0$に対して，ある$x\in A$が存在して
\begin{align*}\alpha-\epsilon<x\le\alpha\end{align*}
が成り立つ．
背理法により示す．すなわち，ある$\epsilon>0$が存在して，任意の$x\in A$に対しても
\begin{align*}\alpha-\epsilon<x\le\alpha\end{align*}
が成り立たないと仮定して矛盾を導く．
この仮定のもとでは，例えば$\alpha-\epsilon$が$A$の上界となっている．
一方，上限の定義から$\alpha$は最小の上界であるが，$\alpha-\epsilon<\alpha$なのでこれは矛盾である．
下限についても同様の定理が成り立ちますが，証明は上限の場合と同様なので省略します．
下に有界な$B\subset\R$に対して$\beta=\inf{B}$とおく．このとき，任意の$\epsilon>0$に対して，ある$x\in B$が存在して
\begin{align*}\beta\le x<\beta+\epsilon\end{align*}
が成り立つ．
上限と下限の存在
集合$A\subset\R$の上限$\sup{A}$は$A$の上界の最小のものとして定義されましたが，$A$が上に有界なら$A$の上界の最小のものはいつでも存在するのでしょうか？
実はこの答えは“Yes”で次が成り立ちます．
集合$A\subset\R$が上に有界なら，必ず$A$の上限$\sup{A}$が$\R$上に存在する．この性質を$\R$の上限性質という．
「公理」と書いたように，実は実数は「上限性質を満たす順序体を実数体$\R$といい，実数体の元を実数という」と定義されます．
そのため，この上限性質は$\R$がもともと満たす性質なので，$A\subset\R$が上に有界な集合であれば安心して上限$\sup{A}$があるとして良いわけですね．
実数の定義について詳しくは以下の記事を参照してください．
上限性質は上限についてしか述べていませんが，上限性質から次のように下限の存在も示すことができます．
集合$A\subset\R$が下に有界なら，必ず$A$の下限$\inf{A}$が$\R$上に存在する．
この上限性質は同値な別の述べ方をされることもあります．それら同値な述べ方も併せて実数の連続性公理といいます．
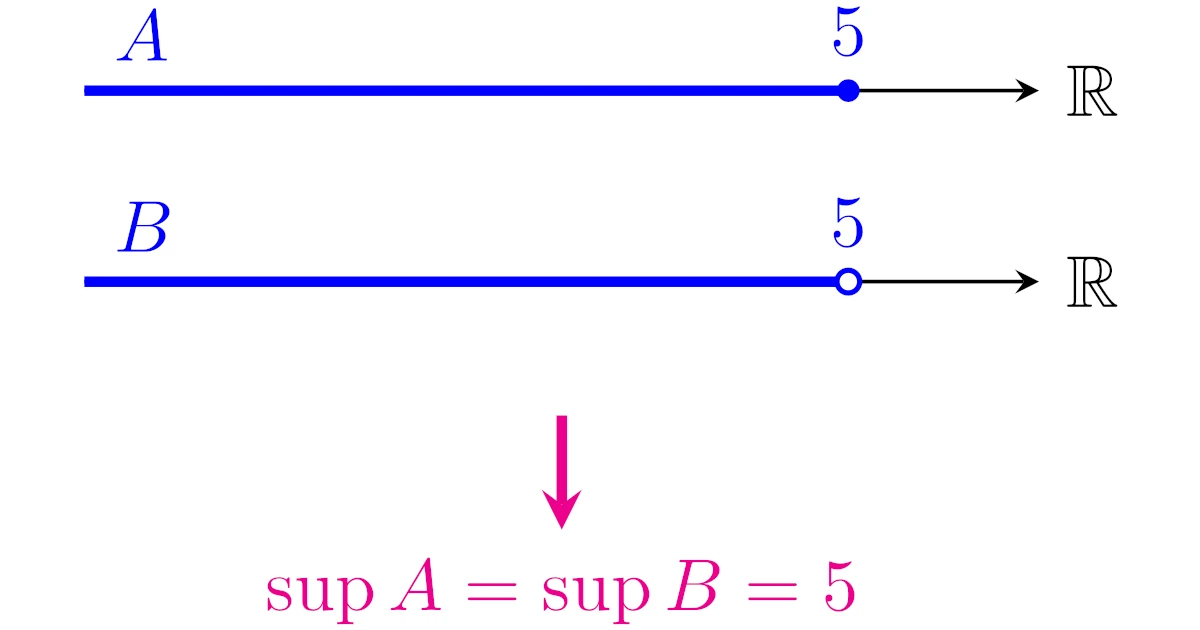
コメント