まずは,次の問題を考えましょう.
集合$A$, $B$をそれぞれ5以下の実数全部の集合,5未満の実数全部の集合とする:
\begin{align*}A=\set{x\in\R}{x\le5},\quad
B=\set{x\in\R}{x<5}.\end{align*}
このとき,集合$A$, $B$の最大値を答えよ.
数学では実数全部の集合を一般に$\R$で表します.そのため,たとえば「$a\in\R$に対して」は「実数$a$に対して」と同じ意味です.
最大値は集合に属していないといけないので,答えは「$A$の最大値は5であり,$B$の最大値は存在しない」となります.
このように5は集合$B$の最大値ではありませんが,$B$でも「5が最大っぽい値」になっているという気持ちはあります.
これら「最大値もしくは最大っぽい値」を上限といい,数学では頻繁に用いられます.同様に「最小値もしくは最小っぽい値」を下限といいます.
この記事では
- 上限と下限の定義
- 上限と下限の具体例
- 上限と下限の基本性質
- 上限と下限の存在性
を順に説明します.
「微分積分学の基本」の一連の記事
上限と下限
ここでは実数の集合の上限と下限の定義と具体例を説明します.
上限の定義
上限を定義するために必要な上界を定義しましょう.
集合$A\subset\R$を考える.$m\in\R$が$A$の上界 (upper bound)であるとは,任意の$a\in A$に対して$a\le m$を満たすことをいう.
また,$A$の上界が存在するとき,$A$は上に有界であるという.
つまり,集合$A$の任意の元以上となっている値$m$を集合$A$の上界というわけですね.
上限の具体例を考えましょう.
集合$A$, $B$を
\begin{align*}A=\set{x\in\R}{x\le5},\quad
B=\set{x\in\R}{x<5}\end{align*}
で定める.このとき,集合$A$, $B$の上界を全てを求めよ.
$A$の上界も$B$の上界も$5$以上の全ての実数である.
この例で大切なことは,$5$は集合$B$の最大値ではありませんが,集合$A$, $B$のどちらも$5$が上界の中で最小のものとなっている点です.
このことをもとに,次のように上限が定義されます.
$A$が上に有界であるとき,上界の最小値を$A$の上限(supremum)または最小上界といい$\sup{A}$と表す.一方,$A$が上に有界でないとき,$\sup{A}=\infty$と定める.
つまり,「『任意の$a\in A$に対して$a\le m$』を満たす$m\in\R$のうち最小のもの」を上限とよぶわけですね.
下限の定義
上限と同様に,下限も次のように定義されます.
$s\in\R$が$A\subset\R$の下界であるとは,任意の$a\in A$に対して$a\ge s$を満たすことをいい,$A$の下界が存在するとき$A$は下に有界であるという.
また,$A$が上に有界であるとき,$A$の下界の最大値を$A$の下限(infimum)または最大下界といい$\inf{A}$と表す.一方,$A$の下界が存在しないときは$\inf{A}=-\infty$と定める.
つまり,集合$A$の任意の元以下となっている値$s$を集合$A$の上界というわけですね.
上限と下限の具体例
具体例を考えてみましょう.
次の$\R$の部分集合それぞれの下限と上限を求めよ.
- $-2$以上$3$未満の実数上の区間$I$
- 正の整数全部の集合$\N$
- $0\le x\le 1$なる有理数$x$全部の集合$X$
(1) $\inf{I}=-2$, $\sup{I}=3$である.
(2) $\inf{\N}=1$, $\sup{I}=\infty$である.
(3) $\inf{X}=0$, $\sup{X}=1$である.
(3)は厳密にはアルキメデスの性質を必要としますが,この記事では省略します.
最大値が存在するときは最大値と上限は一致し,最小値が存在するときは最小値と下限は一致しますね.
上限と下限の基本性質
次に上限と下限に関する次の基本性質を示しておきましょう.
上に有界な$A\subset\R$に対して$\alpha=\sup{A}$とおく.このとき,任意の$\epsilon>0$に対して,ある$x\in A$が存在して
\begin{align*}\alpha-\epsilon<x\le\alpha\end{align*}
が成り立つ.
背理法により示す.すなわち,ある$\epsilon>0$が存在して,任意の$x\in A$に対しても
\begin{align*}\alpha-\epsilon<x\le\alpha\end{align*}
が成り立たないと仮定して矛盾を導く.
この仮定のもとでは,例えば$\alpha-\epsilon$が$A$の上界となっている.
一方,上限の定義から$\alpha$は最小の上界であるが,$\alpha-\epsilon<\alpha$なのでこれは矛盾である.
下限についても同様の定理が成り立ちますが,証明は上限の場合と同様なので省略します.
下に有界な$B\subset\R$に対して$\beta=\inf{B}$とおく.このとき,任意の$\epsilon>0$に対して,ある$x\in B$が存在して
\begin{align*}\beta\le x<\beta+\epsilon\end{align*}
が成り立つ.
上限と下限の存在
集合$A\subset\R$の上限$\sup{A}$は$A$の上界の最小のものとして定義されましたが,$A$が上に有界なら$A$の上界の最小のものはいつでも存在するのでしょうか?
実はこの答えは“Yes”で次が成り立ちます.
集合$A\subset\R$が上に有界なら,必ず$A$の上限$\sup{A}$が$\R$上に存在する.この性質を$\R$の上限性質という.
「公理」と書いたように,実は実数は「上限性質を満たす順序体を実数体$\R$といい,実数体の元を実数という」と定義されます.
そのため,この上限性質は$\R$がもともと満たす性質なので,$A\subset\R$が上に有界な集合であれば安心して上限$\sup{A}$があるとして良いわけですね.
実数の定義について詳しくは以下の記事を参照してください.

上限性質は上限についてしか述べていませんが,上限性質から次のように下限の存在も示すことができます.
集合$A\subset\R$が下に有界なら,必ず$A$の下限$\inf{A}$が$\R$上に存在する.
この上限性質は同値な別の述べ方をされることもあります.それら同値な述べ方も併せて実数の連続性公理といいます.

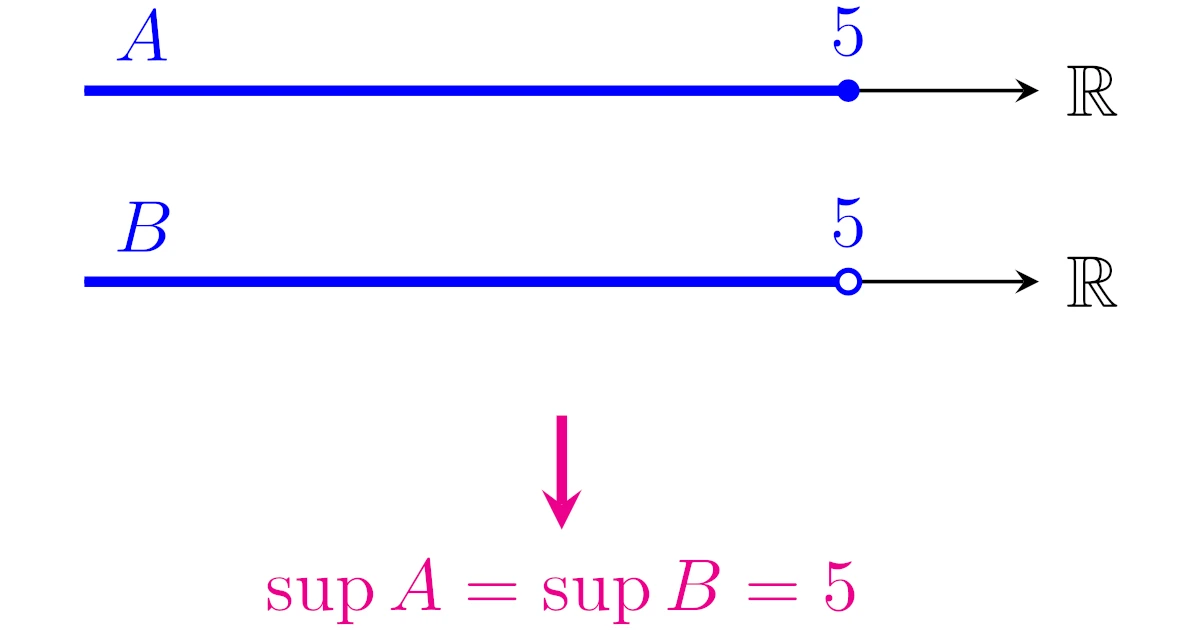

コメント