 複素解析
複素解析 ディリクレ積分を複素積分で計算する|sin(x)/xの広義積分
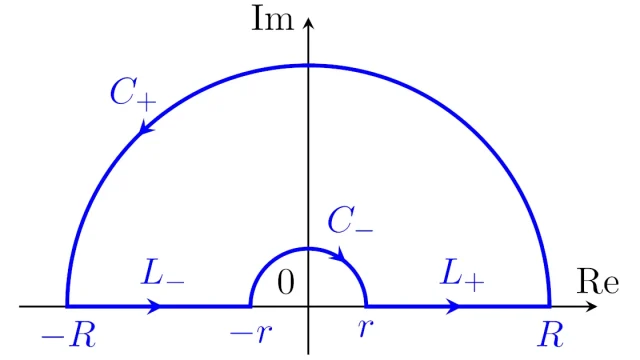
0≦xでのsin(x)/xの広義リーマン積分を「ディリクレ積分」といいます.この記事では,ディリクレ積分を複素積分に持ち込み,コーシーの積分定理を用いることにより,ディリクレ積分がπ/2に収束することを示します.
 複素解析
複素解析 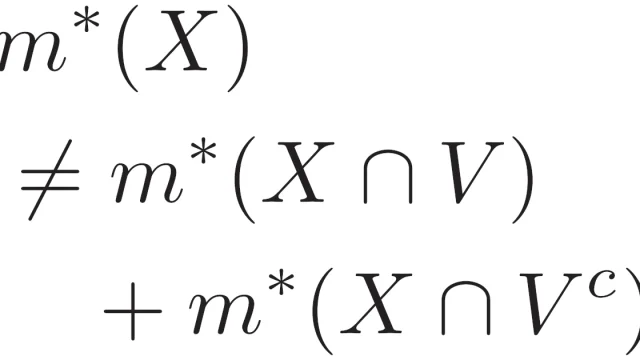 ルベーグ積分
ルベーグ積分 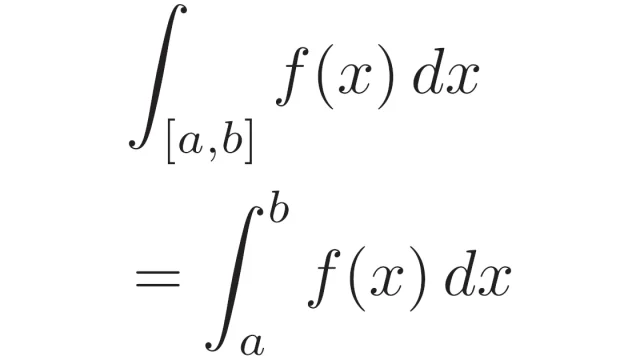 ルベーグ積分の基本
ルベーグ積分の基本 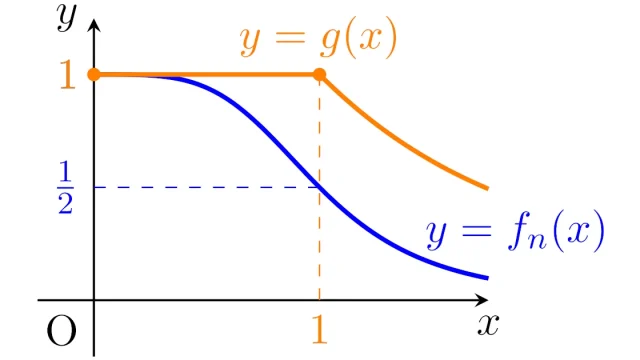 ルベーグ積分の基本
ルベーグ積分の基本 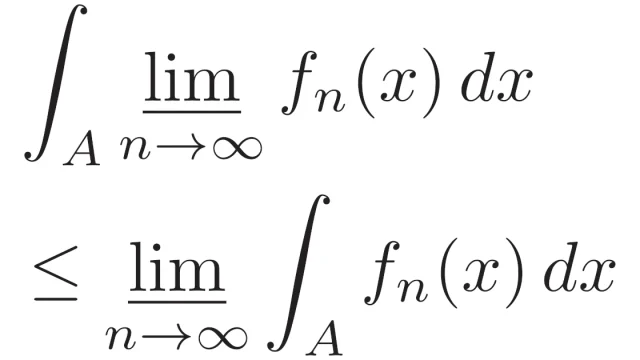 ルベーグ積分の基本
ルベーグ積分の基本 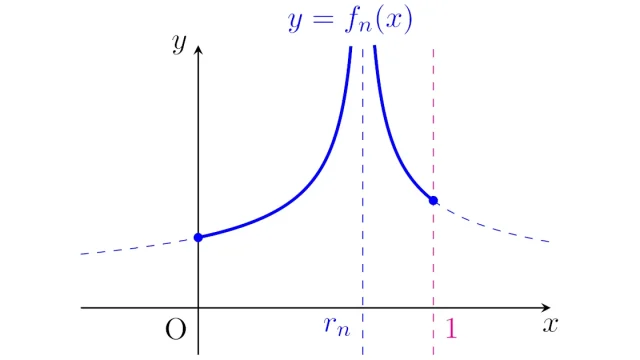 ルベーグ積分の基本
ルベーグ積分の基本 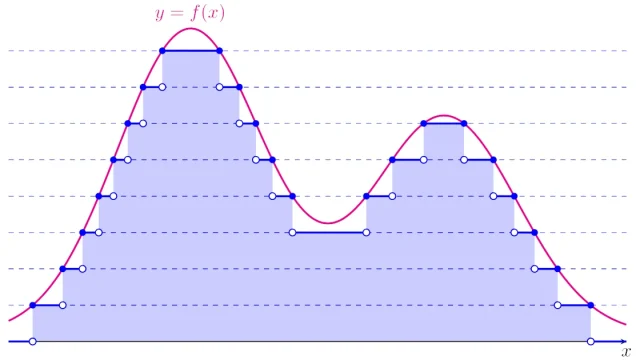 ルベーグ積分の基本
ルベーグ積分の基本 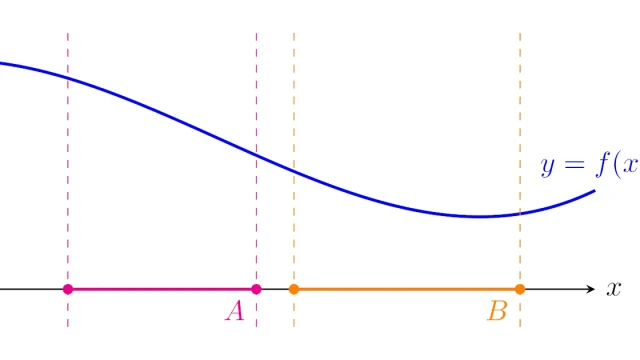 ルベーグ積分の基本
ルベーグ積分の基本 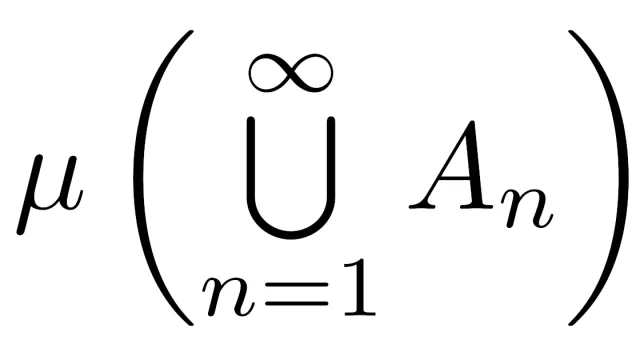 測度論
測度論  測度論
測度論