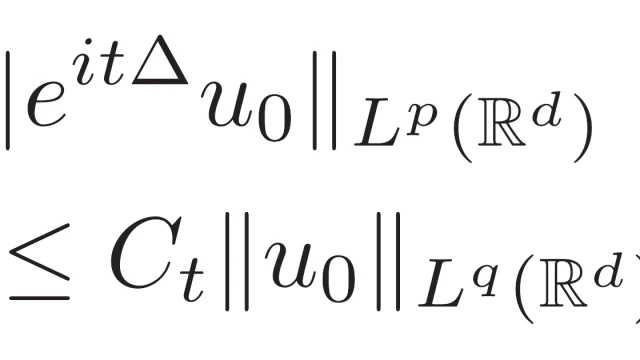 微分方程式
微分方程式 シュレディンガー方程式の分散性|基本解のLpLq評価の導出
シュレディンガー方程式の基本解に関してLpLq評価という基本的な不等式があります.LpLq評価はシュレディンガー方程式を考える上で重要なストリッカーツ評価のベースとなります.
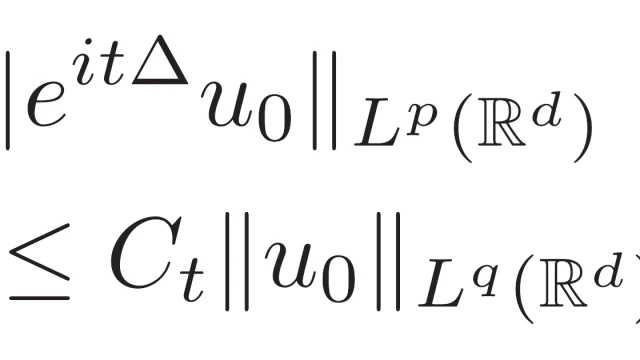 微分方程式
微分方程式 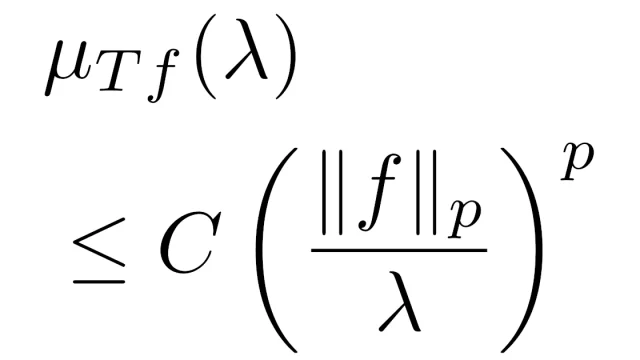 関数解析
関数解析 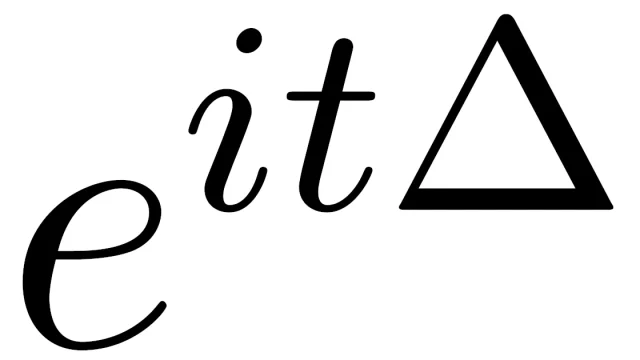 微分方程式
微分方程式  関数解析
関数解析 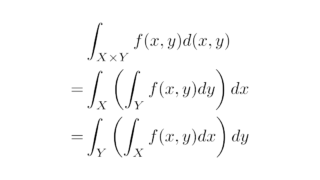 ルベーグ積分
ルベーグ積分 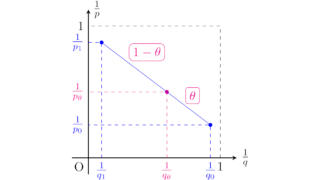 関数解析
関数解析  関数解析
関数解析 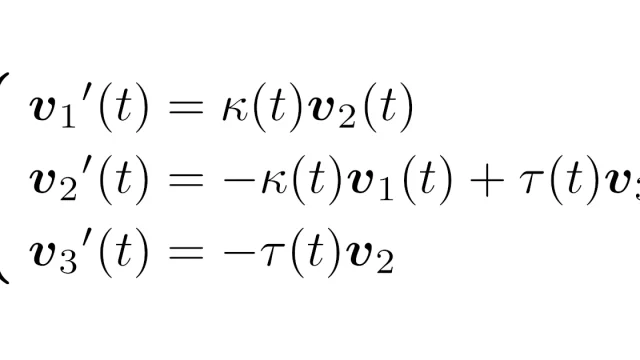 ベクトル解析
ベクトル解析