 位相空間論
位相空間論 連結だが弧状連結でない集合|ℝ²での具体例とその証明
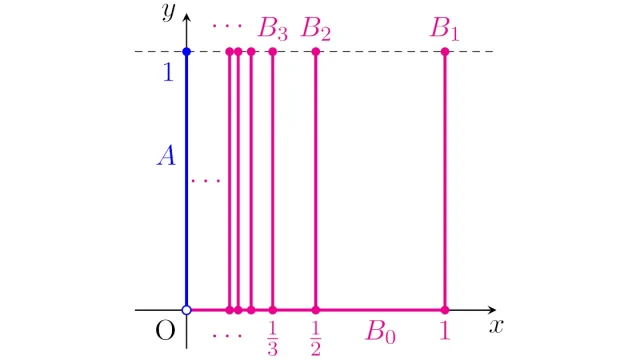
位相空間において,集合がひとまとまりになっていることを表す概念として弧状連結性・連結性があります.一般に弧状連結なら連結ですが,逆は成り立ちません.この記事では「連結だが弧状連結でない集合」の具体例を紹介します.
 位相空間論
位相空間論  位相空間論
位相空間論  位相空間論
位相空間論  位相空間論
位相空間論  位相空間論
位相空間論  位相空間論
位相空間論  位相空間論
位相空間論