そもそも「相関」とは？「共分散」で相関の正負を考える

前々回の記事ではデータを要約する代表値として平均値と中央値を説明し，前回の記事ではデータのばらつきを表す分散を説明しました．

これら前回，前々回の記事で扱った平均値，中央値，分散は，例えば「テストの成績」のように１種類のデータに関するものでした．

この記事では

勉強時間
テストの成績

のように２種類の関係するデータを扱います．

「勉強時間」が長いほど「テストの成績」は高いことは予想できますが，この関係を数値を用いて表すために共分散や相関係数といった統計量を用います．

また，２種類の関係するデータは$xy$平面上に点で表すことができ，このようにしてできる図を散布図といいます．

長くなってしまうので相関係数は次の記事に説明するとして，この記事では

「相関」とは何か？
「共分散」とは何か？

を説明します．

「統計学」の一連の記事

基本の統計量

回帰直線

推定
1. e1 不偏分散ってなに？｜不偏推定量を考え方から理解する
2. e2 尤度関数の考え方｜データから分布を推定する最尤推定法の例

相関
共分散
参考文献
1. 改訂版統計検定２級対応統計学基礎

相関

あるテストを受けた８人の生徒について

勉強時間$x$
テストの点数$y$

が以下の表のようになったとしましょう．

勉強時間$x$とテストの点数$y$
人	A	B	C	D	E	F	G	H
勉強時間$x$	2	6	8	3	13	10	5	9
テストの点数$y$	24	60	63	40	92	85	43	49

散布図

この勉強時間$x$とテストの点数$y$のデータは

横軸を勉強時間$x$
縦軸をテストの点数$y$

として，下図のように$xy$平面上に図示することができます．

このように，２つのデータの組$(x,y)$を$xy$平面上にプロットした図を散布図といい，原因となる$x$を説明変数，その結果となる$y$を目的変数などといいます．

相関

上の散布図を見たとき，点の集まりは右上がりの傾向があるように見えますね．

つまり，「勉強時間が長いほど，テストの点数が高い傾向がある」ということが見てとれます．

このように，２種類のデータ$x$, $y$があったとき，一方のデータが大きいときに他方のデータも大きい傾向があることを正の相関があるといいます．

一方で，２種類のデータ$x$, $y$があったとき，一方のデータが大きいときに他方のデータが小さい傾向があることを負の相関があるといいます．

これら正の相関と負の相関を併せて相関関係や単に相関といいます．

[正の相関]

Rendered by QuickLaTeX.com

[負の相関]

Rendered by QuickLaTeX.com

他にも，例えば

「プールの利用者数」と「アイスの売り上げ」は正の相関
「気温」と「インフルエンザの患者数」は負の相関

があることが予想できますね．

相関関係と因果関係

相関関係と因果関係はしっかり区別しておく必要があります．

例えば，１日の「プールの利用者数」と「アイスの売り上げ」のデータをとったとき

「気温」が高くなれば「プールの利用者数」と「アイスの売り上げ」の両方が上がる
「気温」が低くなれば「プールの利用者数」と「アイスの売り上げ」の両方が下がる

ので，これらには正の相関があることでしょう．

しかし，「プールの利用者数が多くなるからアイスの売り上げが上がる」わけではないし，この逆の「アイスの売り上げが上がるからプールの利用者数が多くなる」わけでもありません．

つまり，「プールの利用者数」と「アイスの売り上げ」の間に相関関係はあっても，因果関係はないことになります．

このように，相関関係があるからからといって，因果関係があるとは限らないことはとても大切です．

このように，相関関係があっても因果関係がないような相関を擬似相関や擬相関などといいます．

擬相関を見破る「偏相関係数」の考え方｜回帰直線から導出

２つの事象に相関があっても因果関係がないことを擬相関といいます．この記事では，相関関係があっても因果関係はないことを見破る指標である偏相関係数を定義し導出します．

共分散

それでは，２つの関係するデータの相関の正負を表す共分散の説明に移ります．

ここでも，先ほどの勉強時間$x$とテストの点数$y$のデータを考えましょう．

勉強時間$x$とテストの点数$y$
人	A	B	C	D	E	F	G	H
勉強時間$x$	2	6	8	3	13	10	5	9
テストの点数$y$	24	60	63	40	92	85	43	49

共分散を求めるためには，まず

$x$の平均$\overline{x}$
$y$の平均$\overline{y}$

を求めます．

$\begin{align*} &\overline{x}=\frac{2+6+8+3+13+10+5+9}{8}=7, \\&\overline{y}=\frac{24+60+63+40+92+85+43+49}{8}=57 \end{align*}$

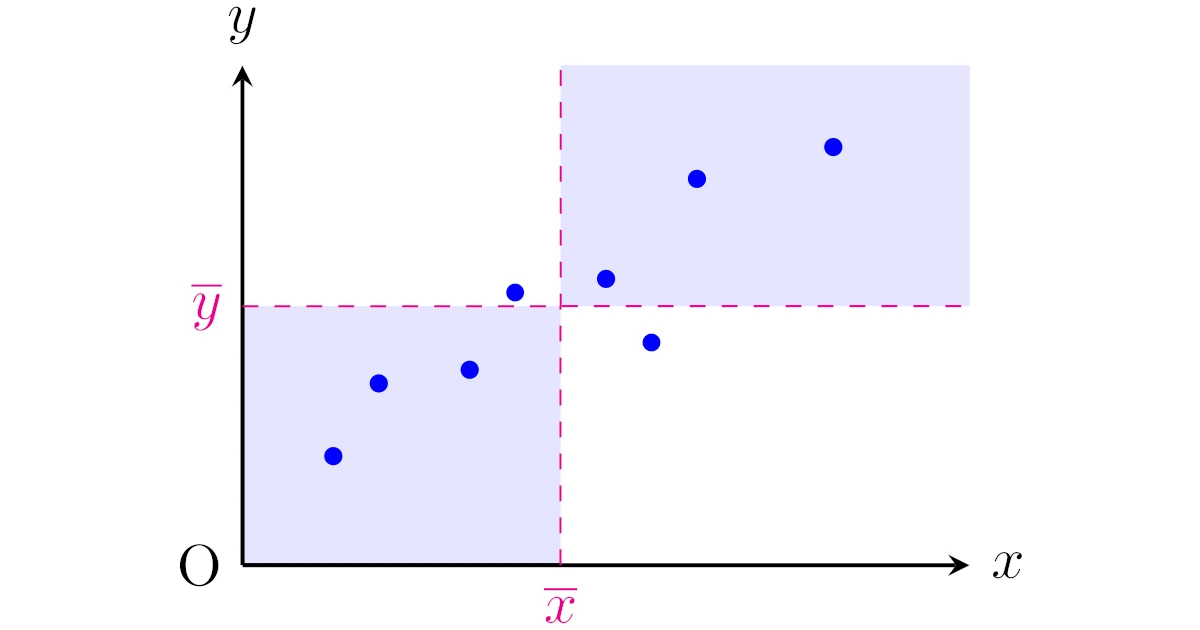
なので，下図のように散布図を４つの領域に分けることができます．

この４つの領域のうち

右上と左下の領域には点が多く
左上と右下の領域には点が少ない

ことが見て取れますが，この「勉強時間」と「テストの点数」の場合でなくとも$x$と$y$に正の相関があるなら右上と左下に点が集まりそうですね！

一方で，$x$と$y$に負の相関があるなら右下と左上に点が集まりそうですね！

[正の相関の場合]

Rendered by QuickLaTeX.com

[負の相関の場合]

Rendered by QuickLaTeX.com

さて，散布図の点$(x_i,y_i)$に対して$(x_i-\overline{x})(y_i-\overline{y})$は$(x_i,y_i)$が４つの領域のどこに入っているかで下図のように変わります．

つまり，

点$(x_i,y_i)$が右上の領域にあるとき，$x_i>\overline{x}$, $y_i>\overline{y}$より$(x_i-\overline{x})(y_i-\overline{y})>0$
点$(x_i,y_i)$が左上の領域にあるとき，$x_i<\overline{x}$, $y_i>\overline{y}$より$(x_i-\overline{x})(y_i-\overline{y})<0$
点$(x_i,y_i)$が左下の領域にあるとき，$x_i<\overline{x}$, $y_i<\overline{y}$より$(x_i-\overline{x})(y_i-\overline{y})<0$
点$(x_i,y_i)$が右下の領域にあるとき，$x_i<\overline{x}$, $y_i<\overline{y}$より$(x_i-\overline{x})(y_i-\overline{y})>0$

となっています．よって

$(x_i-\overline{x})(y_i-\overline{y})>0$となる点$(x_i,y_i)$が多いほど正の相関
$(x_i-\overline{x})(y_i-\overline{y})<0$となる点$(x_i,y_i)$が多いほど負の相関

と言えそうですね．このことから，共分散を次のように定義します．

[共分散]　２種類のデータ$x_1,x_2,\dots,x_n$と$,y_1,y_2,\dots,y_n$に対して，それぞれの平均を$\overline{x}$, $\overline{y}$とする．このとき，このデータの組$(x,y)$の共分散 (covariance)$C_{xy}$を

$\begin{align*} C_{xy} =&\frac{(x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+\dots+(x_n-\overline{x})(y_n-\overline{y})}{n} \\\biggl(=&\frac{1}{n}\sum_{k=1}^{n}(x_i-\overline{x})(y_i-\overline{y})\biggr) \end{align*}$

で定義する．

共分散$C_{xy}$は$Cov_{xy}$などと表すこともよくあります．この共分散$C_{xy}$の定義から

共分散$C_{xy}>0$が正なら$(x_i-\overline{x})(y_i-\overline{y})>0$となるデータの組$(x_i,y_i)$が多い
共分散$C_{xy}<0$が負なら$(x_i-\overline{x})(y_i-\overline{y})>0$となるデータの組$(x_i,y_i)$が多い

ということになるので

$C_{xy}>0$であれば２種類のデータは正の相関がある
$C_{xy}<0$であれば２種類のデータは負の相関がある

と解釈できますね．

具体的に上の勉強時間$x$とテストの点数$y$の共分散を求めましょう．

$\overline{x}=7$, $\overline{y}=57$であることから

$\begin{align*} C_{xy} =&\frac{1}{8}\{(2-7)(24-57)+(6-7)(60-57) \\&\qquad+(8-7)(63-57)+(3-7)(40-57)+(13-7)(92-57) \\&\qquad+(10-7)(85-57)+(5-7)(43-57)+(9-7)(49-57)\} \\=&\frac{165-3+6+68+210+84+28-16}{8} \\=&\frac{271}{4} =67.75 \end{align*}$