複素関数を複素積分で表す公式としてコーシー(Cauchy)の積分公式というものがあります.
このコーシーの積分公式は複素関数のテイラー展開とローラン展開のベースとなる非常に重要な公式です.
初見ではコーシーの積分公式はどうして成り立つのか分かりにくいですが,実はコーシーの積分定理を理解していると直感的に理解することができます.
この記事では
- コーシーの積分公式
- コーシーの積分公式と直感的な考え方
- コーシーの積分公式の証明
を順に説明します.
「複素解析の基本」の一連の記事
コーシーの積分公式と直感的な考え方
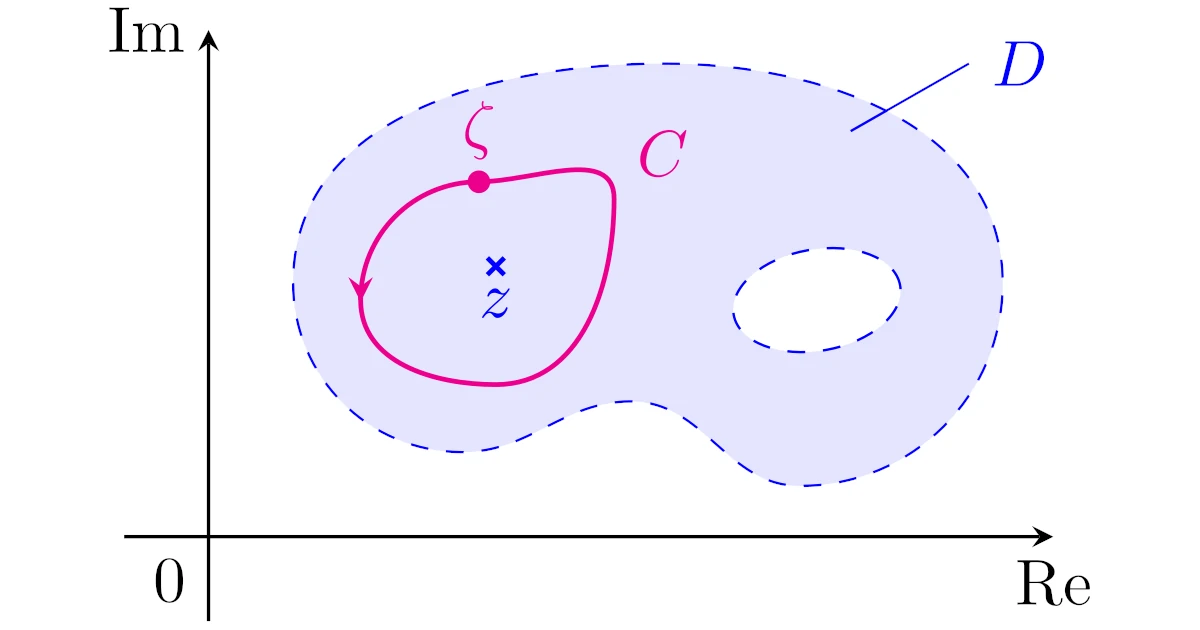
コーシーの積分公式は$D$上の正則関数$f$に対して,任意の点$z\in D$での値$f(z)$を$z$の周りの複素積分で表す公式です.
[コーシーの積分公式]領域$D$上の正則関数$f$を考える.任意の$z\in D$に対して,$z$を内部に含む$D$内の閉曲線$C$を考え,$C$の内部でも$f$が正則なら
\begin{align*}f(z)=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
が成り立つ.ただし,$C$の向きは正方向とする.
右辺の積分変数は$\zeta$なので,$\zeta$が$z$周りの閉曲線$C$上を動くことに注意してください.
分母$2\pi i$を払って
\begin{align*}2\pi if(z)=\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
とみれば,正則関数$f$の$z$での値$f(z)$の$2\pi i$が複素積分$\dint_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta$で求まるという言い方もできますね.
コーシーの積分公式の直感的な考え方
コーシーの積分公式を理解するためには,
- 複素積分の積分経路の変形
- $1/\zeta$の原点周りでの複素積分
が鍵となります.
複素積分の積分経路の変形
コーシーの積分定理を用いると積分経路を変形することができるのでした.
[コーシーの積分定理の応用]領域$D$上の正則関数$g$,$D$上の閉曲線$C$, $C’$を考える.$C$を$D$内部で連続的に変形させて$C’$となるとき,次の等式が成り立つ.
\begin{align*}\int_{C}g(z)\,dz=\int_{C’}g(z)\,dz.\end{align*}
標語的には「複素関数が正則な領域内では,閉積分経路$C$を連続的に変形させても複素積分の値は変化しない」と言えますね.
${1/\zeta}$の原点周りでの複素積分
次の複素積分はよく現れるので覚えておいてよいでしょう.
複素平面上の原点中心の正方向の円周$C$に対して,次が成り立つ.
\begin{align*}\int_{C}\frac{1}{\zeta}\,d\zeta=2\pi i.\end{align*}
円周$C$の半径を$r$とすると,$\zeta\in C$が$\zeta=r(\cos{\theta}+i\sin{\theta})$と表せることから複素積分が計算できますね.
コーシーの積分公式の直感的な理解
コーシーの積分公式はいまの2つの補題から直感的に理解することができます.
まず,$z$を囲む閉曲線$C$を領域$D$上を連続に$z$中心の円周$C’$に変形すると,[コーシーの積分定理の応用]の補題から
\begin{align*}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta=\int_{C’}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
ですね.
この円周$C’$の半径の大きさによらず成り立ちますから,円周$C’$の半径を非常に小さくとってもよいですね.
円周$C’$の半径が十分に小さいときは,任意の$\zeta\in C’$は中心$z$に十分近く$f(\zeta)\approx f(z)$と近似でき,
\begin{align*}\int_{C’}\frac{f(\zeta)}{\zeta-z}\,d\zeta
\approx\int_{C’}\frac{f(z)}{\zeta-z}\,d\zeta
=f(z)\int_{C’}\frac{1}{\zeta-z}\,d\zeta\end{align*}
となります.最後の複素積分$\dint_{C’}\dfrac{1}{\zeta-z}\,d\zeta$は,2つ目の補題で関数も積分経路も$z$平行移動したものなので
\begin{align*}\int_{C’}\frac{1}{\zeta-z}\,d\zeta=2\pi i\end{align*}
となりますから,まとめると
\begin{align*}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta\approx f(z)\cdot2\pi i
\iff f(z)\approx \dfrac{1}{2\pi i}\dint_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
となることが分かります.
途中の近似$\approx$では$C’$の半径を小さくすればするほど誤差が0に近付きますから,実は$\approx$ではなく$=$で成り立つというわけですね.
コーシーの積分公式の証明
コーシーの積分公式の証明は,いま説明した直感的な考え方の近似の部分をきちんと議論すれば完成です.
[コーシーの積分公式]領域$D$上の正則関数$f$を考える.任意の$z\in D$に対して,$z$を内部に含む$D$内の閉曲線$C$を考え,$C$の内部でも$f$が正則なら
\begin{align*}f(z)=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
が成り立つ.ただし,$C$の向きは正方向とする.
分母を払った
\begin{align*}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta=2\pi i f(z)\end{align*}
を示せばよい.左辺から右辺を引いて絶対値をとれば,
\begin{align*}\abs{\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta-2\pi if(z)}
=&\abs{\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta-\int_{C}\frac{f(z)}{\zeta-z}\,d\zeta}
\\=&\abs{\int_{C}\frac{f(\zeta)-f(z)}{\zeta-z}\,d\zeta}\end{align*}
なので$\abs{\dint_{C}\frac{f(\zeta)-f(z)}{\zeta-z}\,d\zeta}=0$を示せば良い.
ここで,任意に$\epsilon>0$をとる.$z$中心の円$C’$の半径$r>0$を十分小さくとれば,次の2つの条件を満たす:
- $C’$の周と内部が$D$に含まれる
- 一般に正則関数は連続なので,$f$は領域$D$上連続だから$C’$上の$\zeta$に対して$|f(\zeta)-f(z)|<\epsilon$である
$C’$は$z$中心,半径$r$の円周なので$\zeta\in C’$は極形式$\zeta-z=r(\cos{t}+i\sin{t})$で表せるから,コーシーの積分定理と併せると
\begin{align*}
\abs{\int_{C}\frac{f(\zeta)-f(z)}{\zeta-z}\,d\zeta}
=&\abs{\int_{C’}\frac{f(\zeta)-f(z)}{\zeta-z}\,d\zeta}
\\=&\abs{\int_{0}^{2\pi}\frac{f(\zeta)-f(z)}{r(\cos{t}+i\sin{t})}\cdot r(-\sin{t}+i\cos{t})\,dt}
\\\le&\int_{0}^{2\pi}\abs{\frac{f(\zeta)-f(z)}{r(\cos{t}+i\sin{t})}\cdot r(-\sin{t}+i\cos{t})}\,dt
\\=&\int_{0}^{2\pi}|f(\zeta)-f(z)|\,dt
<\int_{0}^{2\pi}\epsilon\,dt
=2\pi\epsilon
\end{align*}
が成り立つ.以上で$\epsilon>0$の任意性より$\abs{\dint_{C}\dfrac{f(\zeta)-f(z)}{\zeta-z}\,d\zeta}=0$を得る.


コメント