\begin{align*}f(z)=c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots\end{align*}
と級数の形で表すことができ,このように関数$f$を無限次の多項式のように表すことを$f$のテイラー展開といいます.
この記事では
- テイラー展開とは何か?
- 正則関数が無限回微分可能であること
- 正則関数がテイラー展開可能であることの証明
を順に説明します.
「複素解析の基本」の一連の記事
テイラー展開とは何か?
テイラー展開を説明する前に整級数を定義しておきましょう.
整級数
大雑把に言えば,整級数とは「無限次の多項式」のことで,詳しくは次のように定義されます.
$\alpha\in\C$に対して
\begin{align*}F(x)=c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots
\bra{=\sum_{n=1}^{\infty}c_n(z-\alpha)^n}\end{align*}
で表される複素関数$F$を$\alpha$中心の整級数(power series)という.ただし,$c_0,c_1,c_2,\dots\in\C$である.
この$\alpha$中心の整級数
\begin{align*}F(x)=c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots\end{align*}
に$z=\alpha$を代入すると,第2項以下は全て0なので収束して$F(\alpha)=c_0$となることが分かります.
また,$z\neq\alpha$であっても$z-\alpha$が0に近ければ,各項$c_n(z-\alpha)^n$は0に近いので$f(z)$は収束しやすそうですね.
どれくらい$z-\alpha$が0から離れても$F(z)$が収束してくれるか(収束半径)は係数$c_0,c_1,c_2,\dots$がどうなっているかで決まります.しかし,収束半径については,多くの場合で微分積分学の場合と同様のことが成り立ち,またこの記事のテーマとは少しズレるので,この記事ではこの程度の説明に留めます.
テイラー展開
テイラー(Taylor)展開は関数を整級数で表すことをいいます.
$\alpha\in\C$に対して,複素平面上のある領域上で関数$f$が
\begin{align*}f(z)=c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots\end{align*}
と整級数で表せるとき,この右辺を$f$の$\alpha$中心のテイラー展開という.また,$f$が$\alpha$中心のテイラー展開で表せるとき,$f$は$\alpha$でテイラー展開可能であるという.
微分積分学で学ぶテイラー展開と同様ですね.
ここで微分積分学のテイラー展開で成り立った次の[テイラーの定理]を思い出しておきましょう.
[テイラーの定理(微分積分学)]$a\in\R$の近くで定義された$n$回微分可能な実数値関数$f$は
\begin{align*}f(x)=a_{0}+a_{1}(x-a)+a_{2}(x-a)^{2}+\dots+a_{n-1}(x-a)^{n-1}+R_{n}(x)\end{align*}
と表せる.
この定理は「$f$の微分可能な回数が大きいほど,$f$を近似できる多項式の次数も大きくなる」と言えますが,ネガティヴに捉えれば「$n$回までしか微分できるか分からなければ,$(n-1)$次までしか近似できない」ということになります.
一方,複素関数では1回でも微分可能ならテイラー展開可能であることを証明できます.すなわち,次が成り立ちます.
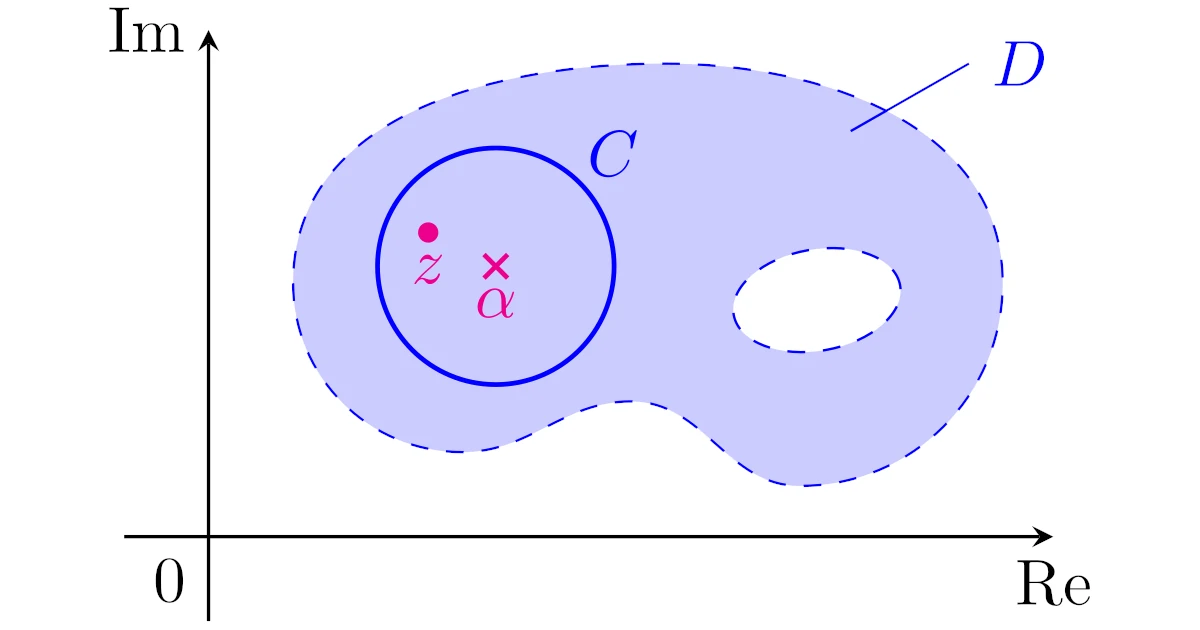
[テイラー展開可能性(複素解析)]領域$D$上の正則関数$f$と$\alpha\in D$を考える.$\alpha$中心の円周$C$の周および内部が$D$に含まれるとき,
\begin{align*}f(z)=c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots&
\\(c_0,c_1,c_2,\dots\in\C)&\end{align*}
と$\alpha$中心でテイラー展開可能である.ただし,$z$は円周$C$の内部の点である.
領域上で1回でも複素微分可能な複素関数を正則関数というのでしたから,「領域$D$上の正則関数は$D$上の任意の点$\alpha$を中心としてテイラー展開可能である」と言っても同じことですね.
このことは複素解析と微分積分学の大きな違いのひとつです.
また,点$z$は円$C$の内部の点なので,このテイラー展開は$C$の内部でのみテイラー展開できることにも注意しておきましょう.
証明はこの記事の最後に遺します.
正則関数が無限回微分可能であること
また,微分積分学では整級数について次が成り立つことも思い出しておきましょう.
[整級数と微分可能性(微分積分学)]$a\in\R$中心の整級数
\begin{align*}F(x)=a_{0}+a_{1}(x-a)+a_{2}(x-a)^{2}+\dots\end{align*}
に対して,ある$r>0$が存在して,$|x-a|<r$なる任意の$x$で$F(x)$が収束するなら,$F$は$a$で無限回微分可能で導関数は
\begin{align*}F'(x)=a_{1}+2a_{2}(x-a)+3a_{3}(x-a)^{2}+\dots\end{align*}
となる.
この補題は$F’$も$|x-a|<r$で収束する整級数となることから証明でき,このことは複素関数に対しても同様に成り立ちます.
領域$D$上の正則関数$f$が$a\in D$の近くでテイラー展開可能という上で示した定理と併せると,$f$はこの定理の$a$で無限回微分可能であることが分かります.すなわち,次の定理が成り立ちます.
微分積分学では「無限回微分可能→テイラー展開可能」の順に話を進めるしかありませんでしたが,複素解析では[整級数と微分可能性]の補題を用いることで「正則関数→テイラー展開可能→無限回微分可能」という順で話を進めることができるので,いま紹介した[正則関数の微分可能性]の定理が成り立つわけですね.
正則関数がテイラー展開可能であることの証明
先ほど述べた[テイラー展開可能性(複素解析)簡略版]を正確に書くと次の通りです.
[テイラー展開可能性(再掲)]領域$D$上の正則関数$f$と$\alpha\in D$を考える.$\alpha$中心の円周$C$の周および内部が$D$に含まれるとき,
\begin{align*}f(z)=c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots&
\\(c_0,c_1,c_2,\dots\in\C)&\end{align*}
と$\alpha$中心でテイラー展開可能である.ただし,$z$は円周$C$の内部の点である.
証明はコーシーの積分公式がベースになります.
$C$の内部の任意の点$z$をとる.コーシーの積分公式より
\begin{align*}f(z)=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
が成り立つ.ただし,$C$の向きは正方向である.右辺の積分の中身は
\begin{align*}\frac{f(\zeta)}{\zeta-z}
&=\frac{f(\zeta)}{\zeta-\alpha}\cdot\frac{1}{\frac{\zeta-z}{\zeta-\alpha}}
\\&=\frac{f(\zeta)}{\zeta-\alpha}\cdot\frac{1}{1-\frac{z-\alpha}{\zeta-\alpha}}\end{align*}
と変形できる.
$|z-\alpha|<|\zeta-\alpha|$より$|\frac{z-\alpha}{\zeta-\alpha}|<1$だから,$\frac{1}{1-\frac{z-\alpha}{\zeta-\alpha}}$は初項1,公比$\frac{z-\alpha}{\zeta-\alpha}$の等比級数である:
\begin{align*}\frac{1}{1-\frac{z-\alpha}{\zeta-\alpha}}=\sum_{k=0}^{\infty}\bra{\frac{z-\alpha}{\zeta-\alpha}}^{k}\end{align*}
よって,
\begin{align*}f(z)&=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-\alpha}\sum_{k=0}^{\infty}\bra{\frac{z-\alpha}{\zeta-\alpha}}^{k}\,d\zeta
\\&=\frac{1}{2\pi i}\int_{C}\sum_{k=0}^{\infty}\frac{f(\zeta)}{\zeta-\alpha}\bra{\frac{z-\alpha}{\zeta-\alpha}}^{k}\,d\zeta\quad\dots(*)\end{align*}
が成り立つ.
ここで,$(*)$の極限(級数)と積分の順序交換をするため,$C$上の複素関数を
\begin{align*}g_n(\zeta):=\sum_{k=0}^{n}\frac{f(\zeta)}{\zeta-\alpha}\bra{\frac{z-\alpha}{\zeta-\alpha}}^{k}\end{align*}
と定め,関数列$\{g_n\}_{n=0}^{\infty}$が$n\to\infty$で$C$上一様収束することをワイエルシュトラスのM判定法を用いて示す.
$C$の半径を$R$とする.円周$C$は有界閉集合(コンパクト集合)なので,$C$上で連続な$f$は最大値$M$をもつから,任意の$\zeta\in C$に対して
\begin{align*}\abs{\frac{f(\zeta)}{\zeta-\alpha}\bra{\frac{z-\alpha}{\zeta-\alpha}}^{k}}\le\frac{M}{R}\bra{\frac{|z-\alpha|}{R}}^{k}\end{align*}
が成り立つ.$\frac{|z-\alpha|}{R}<1$だから級数$\sum_{k=0}^{\infty}\frac{M}{R}(\frac{|z-\alpha|}{R})^{k}$は収束するので,WeierstrassのM判定法より関数列$\{g_n\}$は一様収束する.
よって,$(*)$で極限(級数)と積分の順序交換ができて
\begin{align*}f(z)=\frac{1}{2\pi i}\sum_{k=0}^{\infty}(z-\alpha)^{k}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta\end{align*}
を得る.$c_{k}=\dfrac{1}{2\pi i}\dint_{C}\dfrac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta$とおくと,
\begin{align*}f(z)&=\sum_{k=0}^{\infty}c_{k}(z-\alpha)^{k}
\\&=c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots\end{align*}
となる.係数$c_k$は$z$によらないから示された.
途中で
- ワイエルシュトラスのMテスト
- 一様収束すれば極限(級数)と積分の順序交換が可能
を用いましたが,これらはリーマン積分と同様に証明することができます.


コメント