バナッハの不動点定理（縮小写像の原理）｜証明と具体例も紹介

写像$f:X\to X$を施しても変化しない点，すなわち$f(x)=x$を満たす点$x\in X$を$f$の不動点といいます．

不動点に関する定理は様々なものがありバナッハ(Banach)の不動点定理もその１つで，簡単には次のように述べられます．

[バナッハの不動点定理（簡略版）]　空でない完備距離空間上の縮小写像は不動点を一意にもつ．

バナッハの不動点定理は縮小写像に関する不動点定理のため，縮小写像の定理とも呼ばれます．

常微分方程式の解の存在と一意性を証明する方法としてピカール(Picard)の逐次近似法がありますが，これは本質的にバナッハの不動点定理から理解することができます．

この記事では

完備距離空間の準備
縮小写像の準備
バナッハの不動点定理の内容と証明
バナッハの不動点定理の応用例

を順に説明します．

前提知識の準備
1. 完備距離空間
2. 縮小写像
バナッハの不動点定理
1. バナッハの不動点定理と証明
2. バナッハの不動点定理の応用例

前提知識の準備

バナッハの不動点定理を説明するために

完備距離空間
縮小写像

について定義を確認しておきます．

完備距離空間

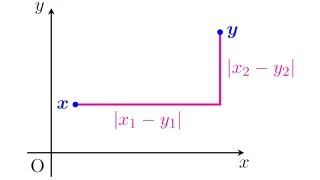
完備距離空間の前にまずは距離空間の定義を確認しておきましょう．

集合$X$に対して，以下の全てを満たす関数$d:X\times X\to\R$を$X$の距離関数または距離 (metrix)という．

$d(x,y)=0 \iff x=y$　(非退化性)
任意の$x,y\in X$に対して$d(x,y)=d(y,x)$　(対称性)
任意の$x,y,z\in X$に対して$d(x,z)\le d(x,y)+d(y,z)$　(劣加法性)

また，組$(X,d)$を距離空間 (metric space)といい，距離$d$が明らかな場合には単に$X$を距離空間という．

３つの条件から任意の$x,y\in X$に対して

$\begin{align*}0=d(x,x)\le d(x,y)+d(y,x)=2d(x,y)\end{align*}$

と$d$の非負値性が成り立ちます．

距離空間について詳しくは以下の記事を参照してください．

距離空間の定義のイメージと具体例｜ノルム空間との関係

数学では３つの条件を満たす集合Xと関数dの組(X,d)を「距離空間」といい，重要な位相空間のひとつです．この記事では，距離空間の定義の３条件のイメージ，距離空間の具体例を説明し，「ノルム空間」との関係も説明します．

さて，距離空間の完備性を説明するためには，Cauchy(コーシー)列が必要です．

距離空間$(X,d)$の点列$\{x_n\}_{n=1}^{\infty}$がCauchy列であるとは，任意の$\epsilon>0$に対して，ある$N\in\N$に対して，$m,n>N$なら$d(x_m,x_n)<\epsilon$が成り立つことをいう．

大雑把に言えば，$X$上の点列$\{x_n\}_{n=1}^{\infty}$がCauchy列であるとは「十分大きく$n$と$m$をとれば，$x_n$と$x_m$をどこまでも近くできる」ということですね．

さて，任意の収束列はCauchy列となるが，逆にCauchy列は$X$上に極限をもつとは限らないのでした．例えば，有理数全体の集合$\Q$と写像

$\begin{align*}d:\Q\times\Q\to\R;(x,y)\mapsto|x-y|\end{align*}$

の組$(\Q,d)$は距離空間ですが，この距離空間$(\Q,d)$でのCauchy列は$\Q$上に極限をもつとは限りません．

実際，$\Q$上の数列$\{x_n\}$を

$x_1=1$
$x_2=1.4$
$x_3=1.41$
$x_4=1.414$
$x_5=1.4142$
……

と実数全体の集合$\R$の中で$\sqrt{2}$に収束するものとして定めると，$\{x_n\}$は$\Q$上のCauchy列ですが$\sqrt{2}\notin\Q$なので，$\Q$に極限を持ちません．

これについて，完備距離空間を次のように定義します．

距離空間$(X,d)$上の任意のCauchy列が$X$上に極限をもつとき，$(X,d)$は完備(complete)であるという．

例えば，Euclid距離空間$(\R^n,d)$は完備距離空間となります．

すなわち，「$m$, $n$を大きくとって$x_m$と$x_n$をいくらでも近くできるなら，その空間の中に$\{x_n\}$の極限が存在する」という性質を満たす距離空間を完備というわけですね．

例えば，実数全体の集合$\R$と写像

$\begin{align*}\tilde{d}:\R\times\R\to\R;(x,y)\mapsto|x-y|\end{align*}$

の組$(\R,\tilde{d})$は完備距離空間です．

先ほどの完備でない距離空間$(\Q,d)$と距離の定義は同様ですが，$(\R,\tilde{d})$の方は完備になります．

例えば，$(\R,\tilde{d})$は$(\Q,d)$上のCauchy列がすべて極限をもつように$(\Q,d)$を拡張したものとなっています．

このように，完備でない距離空間$(X,d)$に対して，これを拡張してできる最小の完備距離空間$(\tilde{X},\tilde{d})$を$(X,d)$の完備化といいます．

縮小写像

距離空間の間の写像$f$について，$f$が縮小写像であるとは以下のように定義します．

距離空間$(X,d)$に対して，写像$f:X\to X$が縮小写像 (contraction)であるとは，ある$p\in(0,1)$が存在して，任意の$x,y\in X$に対して

$\begin{align*}d(f(x),f(y))\le pd(x,y)\end{align*}$

が成り立つことをいう．

つまり，距離空間上の２点を$f$で飛ばして２点の距離が常に$p<1$倍以下になるときに，縮小写像というわけですね．

注意として，定義式の$d(f(x),f(y))\le pd(x,y)$は$d(f(x),f(y))<d(x,y)$とは微妙に異なり，

$\begin{align*}&d(f(x),f(y))\le pd(x,y) \\\Ra\ &d(f(x),f(y))<d(x,y)\end{align*}$

は真ですが，この逆は成り立ちません．

$d(f(x),f(y))\le pd(x,y)$の場合には$x\neq y$なら$\dfrac{d(f(x),f(y))}{d(x,y)}\le p$なので，比率の上限が１になることはありません：

$\begin{align*}\sup_{\substack{x,y\in X\\x\neq y}}\frac{d(f(x),f(y))}{d(x,y)}\le p<1.\end{align*}$

一方，$d(f(x),f(y))<d(x,y)$の場合には$x\neq y$なら$\dfrac{d(f(x),f(y))}{d(x,y)}<1$なので，比率の上限が１になることもあります：

$\begin{align*}\sup_{\substack{x,y\in X\\x\neq y}}\frac{d(f(x),f(y))}{d(x,y)}\le 1.\end{align*}$

よって，単に２点の距離を縮めるだけではなく，２点の距離の拡大率がある$p<1$未満になっているとき縮小写像というわけですね．

また，縮小写像の連続性については次が言えます．

縮小写像はリプシッツ(Lipschitz)連続である．したがって，連続写像である．

バナッハの不動点定理

準備ができたので，本題の説明に移りましょうす．

バナッハの不動点定理と証明

次の定理をバナッハの不動点定理または縮小写像の原理といいます．

[バナッハの不動点定理]　空でない完備距離空間$(X,d)$上の縮小写像$f$は不動点を一意にもつ．

また，この不動点を$x_0$とすると，任意の$x\in X$に対して

$\begin{align*}x_0=\lim\limits_{n\to\infty}f^n(x)\end{align*}$

が成り立つ．ここに，写像$f^n$は$f$を$n$回施す写像である．

縮小写像によって空間が全体的にキュッと集まってくるので，ある１点以外では同じ点に留まることができないというイメージです．

そのため，$X$上のどんな点も$f$を繰り返し施すと，その不動点にどんどん近づいていくというわけですね．

証明を表示

$f$は縮小写像だから，ある$p\in(0,1)$が存在して，任意の$x,y\in X$に対して

$\begin{align*}d(f(x),f(y))\le pd(x,y)\end{align*}$

が成り立つ．

任意に点$x_0\in X$をとり，

$\begin{align*}f(x_n)=x_{n+1}\end{align*}$

によって帰納的に$X$上の点列$\{x_n\}_{n=0}^{\infty}$を定める．

以下，３つのステップに分けて不動点定理の証明を行う．

[１]　点列$\{x_n\}_{n=0}^{\infty}$が極限を持つことを示す．

任意の$\epsilon>0$をとる．任意の$m,n\in\N$ ($m>n$)に対して，$d$の劣加法性より

$\begin{align*} d(x_m,x_n) \le& d(x_m,x_{m-1})+d(x_{m-1},x_{n}) \\\le& d(x_m,x_{m-1})+d(x_{m-1},x_{m-2})+d(x_{m-2},x_{n}) \\&\vdots \\\le& d(x_m,x_{m-1})+d(x_{m-1},x_{m-2})+\dots+d(x_{n+1},x_{n}) \end{align*}$

である．また，任意の$k\in\N$に対して，

$\begin{align*} d(x_{k+1},x_k) =&d(f(x_k),f(x_{k-1})) \le p d(x_k,x_{k-1}) \\=&p d(f(x_{k-2}),f(x_{k-3})) \le p^2 d(x_{k-2},x_{k-3}) \\&\vdots \\=&p^{k-1} d(f(x_1),f(x_0)) \le p^k d(x_1,x_0) \end{align*}$

である．これらを併せて，$p\in(0,1)$に注意すると，

$\begin{align*} d(x_m,x_n) \le& p^{m-1}d(x_1,x_0)+p^{m-2}d(x_1,x_0)+\dots+p^n d(x_1,x_0) \\=&\frac{p^n d(x_1,x_0)\bra{1-p^{m-n}}}{1-p} \\\le&\frac{p^n d(x_1,x_0)(1-0^{m-n})}{1-p} =\frac{p^n d(x_1,x_0)}{1-p} \end{align*}$

である．よって，$n\ge\log_{p}\frac{(1-p)\epsilon}{2d(x_1,x_0)}$となる最小の$n$を$N$とすると，$m,n>N$のとき

$\begin{align*} d(x_m,x_n) \le\frac{\epsilon}{2} <\epsilon \end{align*}$

となるから，$\{x_n\}_{n=0}^{\infty}$はCauchy列である．

距離空間$(X,d)$は完備だから，Cauchy列$\{x_n\}_{n=0}^{\infty}$は極限$x:=\lim\limits_{n\to\infty}x_n$をもつ．

[２]　極限$x$が$f$の不動点であることを示す．

上の命題で示したように，$f$は連続写像だから，

$\begin{align*} f(x_n)=x_{n+1} \Ra\ &\lim_{n\to\infty}f(x_n)=\lim_{n\to\infty}x_{n+1} \\\iff&f\bra{\lim_{n\to\infty}x_n}=\lim_{n\to\infty}x_{n+1} \\\iff&f(x)=x \end{align*}$

が成り立つ．よって，$x$は$f$の不動点である．

[３]　$f$の不動点が唯一つであることを示す．

$x,y\in X$を$f$の不動点とすると，

$\begin{align*} d(x,y) =d(f(x),f(y)) \le pd(x,y) \end{align*}$

だから，$(1-p)d(x,y)\le0$である．

また，もとより$0\le(1-p)d(x,y)$だから$(1-p)d(x,y)=0$なので，$1-p\neq0$に注意すると$d(x,y)=0$を得る．

よって，非退化性より$x=y$となって不動点は唯一つである．

バナッハの不動点定理の応用例

具体的に，以下のような問題を解くことができます．

$x$, $y$の連立方程式

$\begin{align*}\begin{cases}x=\frac{1}{2}\sin{y}\\y=\frac{1}{3}\sin{x}\end{cases}\end{align*}$

の解が$(x,y)=(0,0)$に限ることを示せ．

$\bmat{0\\0}\in\R^2$が$f$の不動点であることは計算からすぐに分かり，バナッハの不動点定理を用いると簡単に不動点の一意性が得られます．

解答を表示

写像$f:\R^2\to\R^2$を

$\begin{align*}f\bra{\bmat{x\\y}}=\bmat{\frac{1}{2}\sin{y}\\\frac{1}{3}\sin{x}}\end{align*}$

で定める．$f$の不動点が$\bmat{0\\0}$に限ることを示せば，連立方程式

$\begin{align*}\begin{cases}x=\frac{1}{2}\sin{y}\\y=\frac{1}{3}\sin{x}\end{cases}\end{align*}$

の解が$(x,y)=(0,0)$に限ることが分かる．

[1]　$\bmat{0\\0}$が$f$の不動点であることを示す．

計算により

$\begin{align*}f\bra{\bmat{0\\0}} =\bmat{\frac{1}{2}\sin{0}\\\frac{1}{3}\sin{0}} =\bmat{0\\0}\end{align*}$

だから，$\bmat{0\\0}$は$f$の不動点である．

[2]　$f$の不動点が唯一つに限ることを示す．

２次元Euclid距離空間$(\R^2,d)$は完備だから，$f$が縮小写像であることを示せば，$f$にバナッハの不動点定理を適用して$f$の不動点はただ１つに限ることが分かる．

$t\in\R$に対して，$|\sin{t}|\le|t|$, $|\cos{t}|\le1$
$a,b\in\R$に対して，和積の公式$\sin{a}-\sin{b}=2\cos{\frac{a+b}{2}}\sin{\frac{a-b}{2}}$

を併せると，$a,b\in\R$に対して

$\begin{align*}(\sin{a}-\sin{b})^2 =&4\bra{\cos{\frac{a+b}{2}}\sin{\frac{a-b}{2}}}^2 \\\le&4\sin^2{\frac{a-b}{2}} \\\le&4\cdot\frac{(a-b)^2}{4} =(a-b)^2\end{align*}$

である．このことに注意すると，任意の$\m{x}=\bmat{a_1\\a_2},\m{y}=\bmat{b_1\\b_2}\in\R^2$に対して

$\begin{align*}d(f(\m{x}),d(\m{y})) =&d\bra{\bmat{\frac{1}{2}\sin{a_2}\\\frac{1}{3}\sin{a_1}},\bmat{\frac{1}{2}\sin{b_2}\\\frac{1}{3}\sin{b_1}}} \\=&\sqrt{\bra{\frac{1}{2}\sin{a_2}-\frac{1}{2}\sin{b_2}}^2+\bra{\frac{1}{3}\sin{a_1}-\frac{1}{3}\sin{b_1}}^2} \\\le&\sqrt{\frac{1}{2^2}(\sin{a_2}-\sin{b_2})^2+\frac{1}{2^2}(\sin{a_1}-\sin{b_1})^2} \\=&\frac{1}{2}\sqrt{(\sin{a_2}-\sin{b_2})^2+(\sin{a_1}-\sin{b_1})^2} \\\le&\frac{1}{2}\sqrt{(a_2-b_2)^2+(a_1-b_1)^2} =\frac{1}{2}d(\m{x},\m{y})\end{align*}$