解が一意でない常微分方程式の具体例｜なぜ解が複数存在するのか

微分方程式
2021.09.06
微分方程式

数学では微分方程式について「解が存在するか」「解が存在すれば一意か」を考えることはよくあります．

常微分方程式の解の存在に関する重要な定理として

があります．

これらの定理は初期条件$u(t_0)=u_0$を満たす微分方程式

    \begin{align*}\od{u}{t}=f(t,u)\end{align*}

の解の存在に関する定理で

  • ペアのの存在定理は解の存在を保証する定理
  • ピカール-リンデレフの定理は解の一意存在を保証する定理

です．

この記事ではこれらのことをふまえ，解が一意ではない常微分方程式を紹介します．

予備知識

解が一意でない微分方程式の例を考える前に，いくつかの予備知識を説明しておきます．

リプシッツ連続性

常微分方程式の解の存在と一意性に関するピカール-リンデレフの定理を述べるために，関数のリプシッツ（Lipschitz）連続性を前もって知っておきたいのでここで説明しておきます．

$\Omega\subset\R$とする．関数$f:\Omega\to\R$がLipschitz連続であるとは，ある$L>0$が存在して，任意の$x,y\in\Omega$に対して，

    \begin{align*}|f(x)-f(y)|\le L|x-y|\end{align*}

を満たすことをいう．

$x\neq y$なら両辺を$|x-y|$で割って

    \begin{align*}\abs{\frac{f(x)-f(y)}{x-y}}\le L\end{align*}

となるので，「$\Omega$上の$f$の平均変化率が有界である」と言ってもいいですね．

リプシッツ連続性の大切なところは$x$, $y$よりも先に$L$がとれるというところです．以下，具体例で確認しましょう．

関数$f:[0,\infty)\to\R;x\mapsto\sqrt{x}$はリプシッツ連続ではないことを示せ．

Rendered by QuickLaTeX.com

リプシッツ連続な関数は平均変化率が有界でしたが，この問題の$f$は原点で「立ち上がる」グラフとなるため平均変化率が有界ではなくリプシッツ連続ではありません．

これをきちんと式で示せば以下のようになります．

$x=0$とし，任意に$y\in(0,\infty)$をとると

    \begin{align*}\abs{\frac{f(x)-f(y)}{x-y}}=\frac{1}{\sqrt{y}}\to\infty\quad(y\to+0)\end{align*}

となるので，任意の$L>0$に対しても，ある十分０に近い$y>0$が存在して

    \begin{align*}|f(0)-f(y)|>L|0-y|\end{align*}

となるので，$f$はリプシッツ連続ではない．

「先にどんなに大きな$L>0$をとったとしても，うまく$x,y\in[0,\infty)$をとれば，$x$から$y$への平均変化率が$L$を超える」ため，問題の$f$はリプシッツ連続ではないわけですね．

２つの解の存在定理

まずは冒頭で紹介した２つの解の存在定理

を紹介します．

［ペアノの存在定理］２変数関数$f:(t,u)\mapsto f(t,u)$は点$(t_0,u_0)\in\R^2$の近傍で連続であるとする．このとき，初期条件$u(t_0)=u_0$を満たす常微分方程式

    \begin{align*}\od{u}{t}=f(t,u)\end{align*}

は初期時刻$t=t_0$の近傍で解が存在する．

［ピカール-リンデレフの定理］２変数関数$f:(t,u)\mapsto f(t,u)$は点$(t_0,u_0)\in\R^2$の近傍で$(t,u)$に関して連続かつ$u$に関してリプシッツ条件を満たすとする．このとき，初期条件$u(t_0)=u_0$を満たす常微分方程式

    \begin{align*}\od{u}{t}=f(t,u)\end{align*}

は初期時刻$t=t_0$の近傍で解が一意に存在する．

ただし，「$f$が$u$に関してリプシッツ条件を満たす」とは，ある$L>0$が存在して，任意の$t$, $u$, $v$に対して，$|f(t,u)-f(t,v)|\le|u-v|$が成り立つことをいう．

よって，$f$が$u$に関してリプシッツ条件まで満たせば一意性が成り立つので，$u$に関してリプシッツ条件を満たさない$f$を考えることで解が一意でない微分方程式が存在する可能性があります．

解が一意でない常微分方程式

それでは解が一意でない常微分方程式を紹介します．

初期条件$u(0)=0$を満たす常微分方程式

    \begin{align*}\od{u}{t}=2\sqrt{u}\end{align*}

の解は一意でない．

この微分方程式の右辺は初期条件の近くで連続なのでペアノの定理から解を持つことが分かりますが，解を複数構成することができ解の一意性が成り立たないことが分かります．

任意に$R>0$をとる．このとき，

    \begin{align*}u(t)=\begin{cases}0&(t<R)\\(t-R)^2&(R\le t)\end{cases}\end{align*}

で定まる関数$u:\R\to\R$は解である．

Rendered by QuickLaTeX.com

実際，$u$は初期条件を満たし，$\R$上微分可能で

    \begin{align*}\od{u}{t}(t)=\begin{cases}0&(t<R)\\2(t-R)&(R\le t)\end{cases}\end{align*}

となるから，$R\le t$で$t-R=\sqrt{(t-R)^2}$となることに注意すれば，$u$が常微分方程式を満たすことが分かる．

いま$R>0$は任意なので，例えば$R=1,2$とすれば解が２つ存在することが分かるから解は一意でない．

この問題では右辺が初期条件$(t,u)=(0,0)$の近くで$u$に関してリプシッツ連続となっていないため，ピカール-リンデレフの定理が適用できません．この点が解の一意性に不都合なわけですね．

なお，同様に$n\in\{2,3,\dots\}$に対して，初期条件$u(0)=0$を満たす常微分方程式

    \begin{align*}\od{u}{t}=nu^{\frac{n-1}{n}}\end{align*}

でも上の問題と同様な解が構成できますから，解に一意性がありませんね．

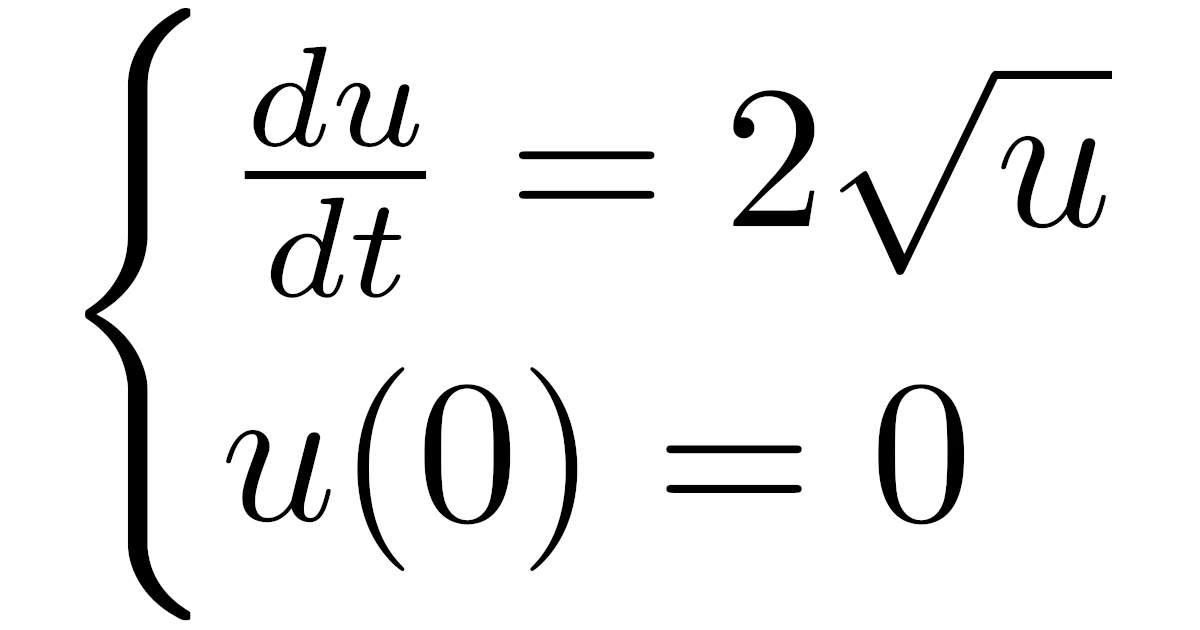
コメント