ピカール-リンデレフの定理｜常微分方程式の解の一意存在定理

微分方程式の初期値問題を考えたとき，

解がそもそもあるか？（存在性）
存在していればひとつか？（一意性）

は微分方程式を考える上で基本的なテーマです．

常微分方程式における解の一意存在に関する重要な定理として，ピカール(Picard)-リンデレフ(Lindelöf)の定理があります．

ピカール-リンデレフの定理の守備範囲は広く，かなり多くの常微分方程式の解の存在と一意性がこの定理から分かります．

この記事では

ピカール-リンデレフの定理の内容
ピカール-リンデレフの定理の証明

を順に説明します．

なお，ピカール-リンデレフの定理は常微分方程式の解を帰納的に近似していくピカールの逐次近似法という手法が背景にあります．

このピカールの逐次近似法については，具体例から考え方を説明している以下の記事を参照してください．

ピカールの逐次近似法｜常微分方程式の解を構成する方法

常微分方程式の解き方は様々なパターンで考えられていますが，常微分方程式がよく知られた形をしていない場合にも，「ピカールの逐次近似法」を用いて解が得られる場合があります．この記事では，具体例からピカールの逐次近似法を説明します．

ピカール-リンデレフの定理
証明のための準備
ピカール-リンデレフの定理の証明
ピカールの逐次近似法との関係

ピカール-リンデレフの定理

少し準備をしてピカール-リンデレフの定理がどのような定理か説明します．

扱う常微分方程式

ピカール-リンデレフの定理を用いると

$\begin{align*} \begin{cases} \od{x_1}{t}(t)=f_1(t,x_1(t),\dots,x_n(t))\\ \qquad\vdots\\ \od{x_n}{t}(t)=f_n(t,x_1(t),\dots,x_n(t)) \end{cases} \end{align*}$

と表せる微分方程式について，右辺の関数が適切な連続性を持てば解の存在と一意性を証明することができます．例えば

$\begin{align*} \od{x}{t}(t)=-tx(t),\quad \od{x}{t}(t)=-tx(t)^2+t^3x(t),\quad \begin{cases} \od{x}{t}(t)=tx(t)+y(t)\\ \od{y}{t}(t)=t^2x(t) \end{cases} \end{align*}$

といったものですね．

この微分方程式はベクトル$\m{x}=\bmat{x_1\\\vdots\\x_n}$, $\m{f}=\bmat{f_1\\\vdots\\f_n}$を用いて

$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$

とベクトルの表記で表せますね．

連立の微分方程式がイメージしにくい場合には，以下では$n=1$として連立でない単一の微分方程式$\od{x}{t}(t)=f(t,x(t))$と思って読んでも本質的に問題ありません．

リプシッツ連続

右辺の関数$\m{f}$に関するリプシッツ(Lipschitz)連続性はピカール-リンデレフの定理が成り立つための条件として本質的に重要なものです．

$\Omega\subset\R^n$とする．関数$\m{f}:\Omega\to\R^n$がリプシッツ連続であるとは，ある$L>0$が存在し，任意の$\m{x},\m{y}\in\Omega$に対して

$\begin{align*}|\m{f}(\m{x})-\m{f}(\m{y})|\le L|\m{x}-\m{y}|\end{align*}$

を満たすことをいう．また，このような$L$のうち最小のものを$f$のリプシッツ定数という．

$\m{x}\neq\m{y}$なら，定義式は

$\begin{align*}\abs{\frac{\m{f}(\m{x})-\m{f}(\m{y})}{\m{x}-\m{y}}}\le L\end{align*}$

と変形できるので，定義域上での平均変化率が有界であるということもできますね．

また，リプシッツ連続であれば一様連続であることも証明できるので，それなりに強い連続性になっています．

例えば，$f:\R\to\R;x\mapsto x^{1/3}$は原点で「立ち上がる」ような関数になっており，リプシッツ連続ではありません．

実際，$x\neq0$なら

$\begin{align*}\abs{\frac{f(x)-f(0)}{x-0}}=\frac{x^{1/3}}{x}=x^{-2/3}\end{align*}$

なので$x$を$0$に近付けると$\abs{\dfrac{f(x)-f(0)}{x-0}}$はどこまでも大きくなりますから，リプシッツ連続の定義を満たしませんね．

このように，変化の激しい箇所があるような関数はリプシッツ連続ではないわけですね．

ピカール-リンデレフの定理

以上の準備のもとでピカール-リンデレフの定理を述べましょう．

[ピカール-リンデレフの定理]　$t_0\in\R$, $\m{x}_0\in\R^n$, $T>0$, $R>0$とする．$\R\times\R^n$上の閉集合$D$を

$\begin{align*}D:=\set{\bmat{t\\\m{x}}\in\R\times\R^n}{ \begin{gathered}|t-t_0|\le T,\\|\m{x}-\m{x}_0|\le R\end{gathered} }\end{align*}$

で定め，関数$\m{f}:D\to\R^n$は$D$上で次を同時に満たすとする．

$\m{f}$は連続
$\m{f}$は$\m{x}$に関してリプシッツ連続

このとき，初期条件$\m{x}(t_0)=\m{x}_0$を満たす常微分方程式

$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$

の解$\m{x}\in(C^1(I))^n$が一意に存在する．ここに，

$I:=[t_0-T^*,t_0+T^*]$
$T^*:=\min\{T,\frac{R}{M}\}$
$M:=\sup\limits_{(t,\m{x})\in D}|\m{f}(t,\m{x})|$

である．さらに，$\m{f}\in(C^m(D))^n$なら，解は$\m{x}\in(C^{m+1}(I))^n$となる．

「関数$\m{f}:D\to\R^n$が$D$上で$\m{x}$に関してリプシッツ連続」であるとは，ある$L>0$が存在し任意の$\bmat{t\\\m{x}_1},\bmat{t\\\m{x}_2}\in D$に対して$|\m{f}(t,\m{x}_1)-\m{f}(t,\m{x}_2)|\le L|\m{x}_1-\m{x}_2|$を満たすことをいいます．

ゴチャゴチャと書かれていて大切な部分が見えにくくなっていますが，「$\m{f}$が２つの条件を満たせば，微分方程式$\dfrac{d\m{x}}{dt}(t)=\m{f}(t,\m{x}(t))$の解が一意に存在する」という点が大切です．

この$\m{f}$の２つの条件はそれほど厳しい条件ではないので，応用上多くの方程式に対してこのピカール-リンデレフの定理は適用できます．

なお，リプシッツ条件が成り立たない場合には解の一意性は保証されないわけですが，解が一意ではない微分方程式の初期値問題については以下の記事を参照してください．

解が一意でない常微分方程式の具体例｜なぜ解が複数存在するのか

「微分方程式に解が存在するか？解が存在すれば一意か？」を考えることはよくあり，解の存在定理はいくつも知られています．この記事では，基本的な解の存在定理を踏まえて解が一意ではない微分方程式の具体例を紹介します．

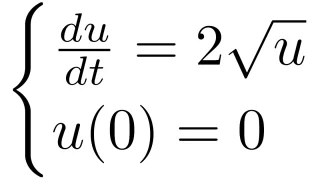
証明のための準備

次に，このピカールの逐次近似法を保証するピカール-リンデレフの定理を説明するためにいくつか準備をしましょう．

一様ノルム

閉区間$I\subset\R$に対して，関数$u:I\to\R$に対して，一様ノルム$\|\cdot\|_I$を

$\begin{align*}\|u\|_I:=\sup_{t\in I}|u(t)|\end{align*}$

で定めます．

$C^0(I)$は$I$上で定義された連続関数全体の集合で，$n$個の成分が全て$C^0(I)$の元であるようなベクトル全体の集合を$(C^0(I))^n$と表します．

これは$n$個の$C^0(I)$の直積で，イメージとしては$\R$の$n$個の直積を$\R^n$と表すのと同じです．

このとき，$n$個の$C^0(I)$の直積$(C^0(I))^n$は一様ノルム$\|\cdot\|_I$によって完備距離空間となります．

バナッハの不動点定理

この記事ではピカール-リンデレフの定理の証明にはバナッハの不動点定理を用います．

[バナッハの不動点定理]　空でない完備距離空間$(X,d)$上の縮小写像$f$は不動点を唯一つもつ．なお，任意の$x\in X$に対して

$\begin{align*}\lim_{n\to\infty}f^n(x)\end{align*}$

が写像$f$の不動点である．ここに，写像$f^n$は$f$を$n$回施す写像である．

バナッハの不動点定理のイメージや証明など，詳しくは以下の記事を参照してください．

バナッハの不動点定理（縮小写像の原理）｜証明と応用例も紹介

バナッハの不動点定理（縮小写像の原理）は「完備距離空間上の縮小写像は唯一つの不動点をもつ」という定理です．この記事では，基本事項を確認したのち，バナッハの不動点定理の具体例を紹介し，定理を証明します．

積分方程式への書き換え

ピカール-リンデレフの定理を証明するためには，同値な積分方程式への書き換えがポイントとなります．

$I\subset\R$を閉区間，$t_0\in I$，$\m{x}_0\in\R^n$とする．このとき，以下の２条件は同値である．

$\m{x}\in(C^1(I))^n$は初期条件$\m{x}(t_0)=\m{x}_0$を満たす常微分方程式
$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$
の解である．
$\m{x}\in(C^0(I))^n$は積分方程式
$\begin{align*}\m{x}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau\end{align*}$
の解である．

[1] 初期条件$\m{x}(t_0)=\m{x}_0$を満たす常微分方程式

$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$

が解$\m{x}\in C^1(I)$をもつとする．

このとき，変数を$\tau$に置き換えて両辺を$\tau$について$[t_0,t]$上で積分すると，微分積分学の基本定理から

$\begin{align*} &\int_{t_0}^{t}\od{\m{x}}{t}(\tau)\,d\tau=\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau \\\iff&\m{x}(t)-\m{x}(t_0)=\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau \\\iff&\m{x}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau \end{align*}$

が成り立つ．

[2] 積分方程式

$\begin{align*}\m{x}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau\end{align*}$

が解$\m{x}\in C^0(I)$をもつとする．

積分方程式に$t=t_0$を代入すると，右辺の積分範囲は$[t_0,t_0]$となって積分値は$0$だから，初期条件$\m{x}(t_0)=\m{x}_0$が得られる．

また，$\m{f}$はもとより$D$上で連続なので，$\m{f}$に連続な$\m{x}$を合成した関数$\m{f}(t,\m{x}(t))$は$t$に関して$I$上で連続となる．

よって，連続関数の積分なので，右辺の$\dint_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau$は$t$に関して$I$上$C^1$級である．

これより，左辺の$\m{x}(t)$も$I$上$C^1$級となって，両辺を$t$で微分すると

$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$

が成り立つ．

このように，$\dfrac{d\m{x}}{dt}(t)=\m{f}(t,\m{x}(t))$の形の常微分方程式を積分方程式に書き直すことができることをDuhamel(デュアメル)の原理といいます．

積分方程式$\m{x}(t)=\m{x}_0+\dint_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau$が自動的に初期条件$\m{x}(t_0)=\m{x}_0$を満たすのはありがたい点です．

以降はこの積分方程式を中心に話を進めていくことになります．

ピカール-リンデレフの定理の証明

それでは，ピカール-リンデレフの定理を５つのステップに分けて証明します．

[ピカール-リンデレフの定理（再掲）]　$t_0\in\R$, $\m{x}_0\in\R^n$, $T>0$, $R>0$とする．$\R\times\R^n$上の閉集合$D$を

$\begin{align*}D:=\set{\bmat{t\\\m{x}}\in\R\times\R^n}{ \begin{gathered}|t-t_0|\le T,\\|\m{x}-\m{x}_0|\le R\end{gathered} }\end{align*}$

で定め，関数$\m{f}:D\to\R^n$は$D$上で次を同時に満たすとする．

$\m{f}$は連続
$\m{f}$は$\m{x}$に関してリプシッツ連続

このとき，初期条件$\m{x}(t_0)=\m{x}_0$を満たす常微分方程式

$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$

の解$\m{x}\in(C^1(I))^n$が一意に存在する．ここに，

$I:=[t_0-T^*,t_0+T^*]$
$T^*:=\min\{T,\frac{R}{M}\}$
$M:=\sup\limits_{(t,\m{x})\in D}|\m{f}(t,\m{x})|$

である．さらに，$\m{f}\in(C^m(D))^n$なら，解は$\m{x}\in(C^{m+1}(I))^n$となる．

ステップ１

$\m{f}$の$\m{x}$に関するリプシッツ連続性のリプシッツ定数を$L$とします．さらに，$I_{L}:=\brc{t_0-\frac{1}{2L},t_0+\frac{1}{2L}}\cap I$とし，関数空間

$\begin{align*}\mathcal{C}:=\set{\m{x}\in(C^0(I_{L}))^n}{\all t\in I_L\quad (t,\m{x}(t))\in D}\end{align*}$

を定めると，$\mathcal{C}$は一様ノルム$\|\cdot\|_{I_L}$に関する空でない完備距離空間となることを示します．

$I_L$上で恒等的に$\m{x}_0$をとる関数は$\mathcal{C}$に属するから$\mathcal{C}\neq\emptyset$である．

一様ノルム$\|\cdot\|_{I_L}$に関するCauchy列$\{\m{x}_k\}_{k\in\N}\subset\mathcal{C}$を任意にとる．このとき，

$\mathcal{C}\subset(C^0(I_L))^n$より，$\{\m{x}_k\}_{k\in\N}$は$(C^0(I_L))^n$における一様ノルム$\|\cdot\|_{I_L}$に関するCauchy列
$(C^0(I_{L}))^n$は一様ノルム$\|\cdot\|_{I_L}$に関して完備距離空間

だから，ある$\m{x}\in(C^0(I_{L}))^n$が存在して$\m{x}=\lim\limits_{k\to\infty}\m{x}_k$を満たす．

任意の$k\in\N$に対して，$\m{x}_k\in\mathcal{C}$だから

$\begin{align*}|\m{x}_k(t)-\m{x}_0|\le M|t-t_0|\end{align*}$

を満たす．よって，左辺で$k\to\infty$として

$\begin{align*}|\m{x}(t)-\m{x}_0|\le M|t-t_0|\end{align*}$

を得る．したがって，$\{\m{x}_k\}_{k\in\N}$の極限が$\mathcal{C}$に属するから，$\mathcal{C}$は完備である．

$\mathcal{C}$は閉集合なので，位相空間の一般論から$\m{x}\in\mathcal{C}$としても良いですね．

ステップ２

$\mathcal{C}$上の写像$\Phi$を

$\begin{align*}\Phi(\m{x})(t):=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau\end{align*}$

で定めると，$\Phi$は$\mathcal{C}$上の縮小写像となることを示します．

[1]　$\Phi$の値域が$\mathcal{C}$であることを示す．

任意に$\m{x}\in\mathcal{C}$をとる．このとき，

任意の$\tau\in I_L$に対して$(\tau,\m{x}(\tau))\in D$を満たすこと
$\m{f}$は$D$上で定義されていること

を併せると，任意の$t\in I_L$に対して$\dint_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau$が定義できる．

よって，積分の連続性から$\Phi(\m{x})\in (C^0(I_L))^n$を得る．

また，$t\in I_L$のとき$|t-t_0|\le T^*$だから

$\begin{align*}|\Phi(\m{x})(t)-\m{x}_0| =&\abs{\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau} \\\le&\abs{\int_{t_0}^{t}M\,d\tau} =M|t-t_0| \\\le&M\cdot T^* \le M\cdot\frac{R}{M} =R\end{align*}$

である．よって，$\Phi(\m{x})\in\mathcal{C}$となる．すなわち，$\Phi:\mathcal{C}\to\mathcal{C}$である．

[2]　$\Phi$が$\mathcal{C}$上の縮小写像であることを示す．

このとき，任意の$\m{x},\m{y}\in\mathcal{C}$に対して，

$\begin{align*}\|\Phi(\m{x})-\Phi(\m{y})\|_{I_L} =&\sup_{t\in I_L}\abs{\int_{t_0}^{t}\{\m{f}(\tau,\m{x}(\tau))-\m{f}(\tau,\m{y}(\tau))\}\,d\tau} \\\le&\sup_{t\in I_{L}}\abs{\int_{t_0}^{t}\abs{\m{f}(\tau,\m{x}(\tau))-\m{f}(\tau,\m{y}(\tau))}\,d\tau} \\\le&\sup_{t\in I_{L}}L\abs{\int_{t_0}^{t}|\m{x}(t)-\m{y}(t)|\,d\tau} \\\le&\sup_{t\in I_{L}}L\abs{\int_{t_0}^{t}\|\m{x}-\m{y}\|_{I_L}\,d\tau} \\\le&L\cdot\frac{1}{2L}\cdot\|\m{x}-\m{y}\|_{I_L} =\frac{1}{2}\|\m{x}-\m{y}\|_{I_L}\end{align*}$

なので，$\Phi$は$\mathcal{C}$上の一様ノルム$\|\cdot\|_{I_L}$に関する縮小写像である．

ステップ３

積分方程式

$\begin{align*}\m{x}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau\end{align*}$

が解$\m{x}\in C^0(I)$をもつことを示します．

ステップ１より$\mathcal{C}$は空でない完備距離空間であり，ステップ２より$\Phi$が$\mathcal{C}$上の縮小写像だから，バナッハの不動点定理より$\Phi$の不動点が$\mathcal{C}$上にただ１つ存在する．すなわち，

$\begin{align*}\m{x}=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau\end{align*}$

を満たす$\m{x}\in\mathcal{C}$が一意に存在する．

もし$\sup I_L<\sup I$なら，$t_0+\frac{1}{2L}$を初期時間とみなせば，これまでと同じ議論により解が$t\le t_0+\frac{2}{2L}$まで延長できる．

これを繰り返すことにより，解の定義域は$t\le t_0+T^*$にまで延長できる．

同様に，$\inf I_L>\inf I$なら，解の定義域は$t_0-T^*\le t$にまで延長できる．

よって，初期条件$\m{x}(t_0)=\m{x}_0$を満たす積分方程式

$\begin{align*}\m{x}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau\end{align*}$

の解$\m{x}\in C^0(I)$が存在する．

ステップ１とステップ２の議論を一回行うごとに，解の存在する$t$が正の方向に$\dfrac{1}{2L}$ずつ延長されていくことになるわけですね．

これで$\mathcal{C}$において積分方程式の解が一意存在することは分かりましたが，より広い$C^0(I)$で解が一意であるかどうかはこの時点では分かっていません．

ステップ４

初期条件$\m{x}(t_0)=\m{x}_0$を満たす常微分方程式

$\begin{align*}\od{\m{x}}{t}(t)=\m{f}(t,\m{x}(t))\end{align*}$

の解$\m{x}$が$C^1(I)$において一意に存在することを示します．

$\m{x},\m{y}\in C^0(I)$を積分方程式の解とし，$\m{u}:=\m{x}-\m{y}$とする．$I$上で恒等的に$\m{u}(t)=0$が成り立つこと，すなわち$\|\m{u}\|_I=0$を示せばよい．

積分方程式の解であることから，任意の$t\in I$に対して

$\begin{align*} &\m{x}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{x}(\tau))\,d\tau, \\&\m{y}(t)=\m{x}_0+\int_{t_0}^{t}\m{f}(\tau,\m{y}(\tau))\,d\tau \end{align*}$

が成り立つ．

また，一般に有界閉区間で連続な関数は最大値を持つから$\|u\|_I<\infty$である．

辺々引いて長さをとると，$\m{f}$のリプシッツ連続性より

$\begin{align*} |\m{u}(t)| =&\abs{\int_{t_0}^{t}\{\m{f}(\tau,\m{x}(\tau))-\m{f}(\tau,\m{y}(\tau))\}\,d\tau} \\\le&\abs{\int_{t_0}^{t}|\m{f}(\tau,\m{x}(\tau))-\m{f}(\tau,\m{y}(\tau))|\,d\tau} \\\le&L\abs{\int_{t_0}^{t}|\m{u}(\tau)|\,d\tau} \le L\abs{\int_{t_0}^{t}\|\m{u}\|_{I}\,d\tau} \\=&L\|\m{u}\|_I|t-t_0| \end{align*}$

となる．よって

$\begin{align*} &|\m{u}(t)|\le L\abs{\int_{t_0}^{t}|\m{u}(\tau)|\,d\tau}\quad\dots(*), \\&|\m{u}(t)|\le L\|u\|_I|t-t_0| \end{align*}$

が得られた．

以下，任意の$N\in\N$に対して$|\m{u}|\le \dfrac{L^{N}\|\m{u}\|_I}{N!}|t-t_0|^{N}$が成り立つことを数学的帰納法により示す．

$N=1$の場合はいま得られたので，あとは$N=k$のときに成り立つと仮定して$N=k+1$の場合を示せばよい．

$N=k$のときに成り立つとすると

$\begin{align*}|\m{u}(t)|\le\frac{L^{k}\|\m{u}\|_I}{k!}|t-t_0|^{k}\end{align*}$

であり，これと不等式$(*)$を併せて

$\begin{align*} |\m{u}(t)| \le& L\abs{\int_{t_0}^{t}\frac{L^{k}\|\m{u}\|_I}{k!}|t-t_0|^{k}\,d\tau} \\=&L\cdot\frac{L^{k}\|\m{u}\|_I}{k!}\cdot\frac{1}{k+1}|t-t_0|^{k+1} \\=&\frac{L^{k+1}\|\m{u}\|_I}{(k+1)!}|t-t_0|^{k+1} \end{align*}$