シュレディンガー(Schrödinger)方程式の基本解に関する基礎的な評価式に$L^pL^q$評価があります.
シュレディンガー方程式の基本解とは,初期値$u_0=u(0,x)$に対する自由シュレディンガー方程式
\begin{align*}i\partial_t{u}(t,x)+\Delta u(t,x)=0\end{align*}
の解$u$のことで,$u,u_0\in\mathcal{S}(\R^d)$のとき解は$u=e^{it\Delta}u_0$と表すことができるのでした.
シュレディンガー方程式の$L^pL^q$評価は
\begin{align*}\|e^{it\Delta}u_0\|_{L^{p}(\R^{d})}\le C_t\|u_0\|_{L^{q}(\R^{d})}\end{align*}
の形の基本解$e^{it\Delta}u_0$のノルムを初期値$u_0$のノルムで上から評価する不等式です.
$L^pL^q$評価を用いると,シュレディンガー方程式に関する重要な評価式であるストリッカーツ(Strichartz)評価を証明することができます.
一連の記事はこちら
【自由シュレディンガー方程式の基本解とユニタリ群】
【シュレディンガー方程式の分散性|基本解のLpLq評価の導出】←今の記事
【シュレディンガー方程式のストリッカーツ評価の導出】
シュレディンガー方程式の基本解の$L^pL^q$評価
まず前回の記事で説明したシュレディンガー方程式の基本解を復習し,$L^pL^q$評価を紹介します.
シュレディンガー方程式の基本解(復習)
[基本解(自由解)]自由シュレディンガー方程式の初期値問題
\begin{align*}\begin{cases}
i\partial_{t}u(t,x)+\Delta u(t,x)=0 & (t,x)\in\R\times\R^d\\
u(0,x)=u_0(x) & x\in\R^d\\
\end{cases}\end{align*}
の解$u$をシュレディンガー方程式の基本解(fundamental solution)または自由解(free solution)という.
自由解は以下のように表されます.
初期条件$u(0,x)=u_0(x)$のシュレディンガー方程式の解は
\begin{align*}e^{it\Delta}u_0(x)
&=\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}\hat{u_0}(\xi)}(x)
\\&=\frac{1}{(4\pi it)^{d/2}}\int_{\R^d}e^{-\frac{|x-y|^2}{4it}}u_0(y)\,dy\end{align*}
と表せる.
初期値$u_0$に対するシュレディンガー方程式の自由解$e^{it\Delta}u_0$を与える作用素$e^{it\Delta}$を自由シュレディンガー発展作用素というのでした.
$L^pL^q$評価
以下,$p\in[1,\infty]$とし,$L^p(\R^d)$ノルムを$\|\cdot\|_p$と表します:
\begin{align*}&\|f\|_p:=\bra{\int_{\R}|f(x)|^p\,dx}^{1/p}\quad(p\in[1,\infty)),
\\&\|f\|_{\infty}:=\operatorname{ess\,sup}_{x\in\R}|f(x)|.\end{align*}
次の評価を$L^pL^q$評価または分散型評価といいます.
[$L^{p}L^{q}$評価]$p\in[2,\infty]$と$u\in L^{q}(\R^{d})$に対して
\begin{align*}\|e^{it\Delta}u\|_{L^{p}(\R^{d})}
\le\bra{4\pi|t|}^{-d(\frac{1}{2}-\frac{1}{p})}\|u\|_{L^{q}(\R^{d})}\end{align*}
が成り立つ.ただし,$q\in[1,2]$は$p$のHölder共役である:$1=\frac{1}{p}+\frac{1}{q}$.
証明は
- $(p,q)=(\infty,1)$の場合($L^{\infty}L^{1}$評価)
- $(p,q)=(2,2)$の場合($L^2$等長性)
を示し,この2つの評価をもとにリース-トーリンの複素補間定理を適用します.
$L^pL^q$評価の証明のための準備
ここで$L^{\infty}L^{1}$評価,$L^2$等長性を証明し,リース-トーリンの複素補間定理を復習しておきます.
$L^{\infty}L^{1}$評価の証明
$(p,q)=(\infty,1)$の場合の$L^{p}L^{q}$評価を示しましょう.
[$L^{\infty}L^{1}$評価]任意の$u\in L^1(\R^d)$に対して,次が成り立つ:
\begin{align*}\|e^{it\Delta}u\|_{L^{\infty}(\R^{d})}\le\bra{4\pi|t|}^{-\frac{d}{2}}\|u\|_{L^{1}(\R^{d})}\end{align*}
$\Bigl|e^{-\frac{|x-y|^2}{4it}}\Bigr|=1$より,
\begin{align*}\|e^{it\Delta}u\|_{L^{\infty}(\R^{d})}
&=\nor{\frac{1}{(4\pi it)^{d/2}}\int_{\R^d}e^{-\frac{|x-y|^2}{4it}}u(y)\,dy}_{L^{\infty}(\R^{d})}
\\&\le\sup_{x\in\R^d}\bra{\frac{1}{|4\pi it|^{d/2}}\int_{\R^d}\Bigl|e^{-\frac{|x-y|^2}{4it}}u(y)\Bigr|\,dy}
\\&=\sup_{x\in\R^d}\bra{\frac{1}{|4\pi t|^{d/2}}\int_{\R^d}|u(y)|\,dy}
\\&=(4\pi|t|)^{-\frac{d}{2}}\|u\|_{L^{1}(\R^{d})}\end{align*}
が従う.
$L^{\infty}L^{1}$評価から,任意の$u_0\in\mathcal{S}(\R^d)$に対して
\begin{align*}\lim_{|t|\to\infty}\|e^{it\Delta}u\|_{L^{\infty}(\R^{d})}=\lim_{|t|\to\infty}(4\pi|t|)^{-\frac{d}{2}}\|u\|_{L^{1}(\R^{d})}=0\end{align*}
となるので,シュレディンガー方程式の基本解は$|t|$が増大するにつれて一様に0に近付きますね.
$L^2$等長性の証明
$(p,q)=(2,2)$の場合の$L^{p}L^{q}$評価($L^2$等長性)を示しましょう.
[$L^{2}L^{2}$評価($L^2$等長性)]任意の$u\in L^2(\R^{d})$に対して,次が成り立つ:
\begin{align*}\|e^{it\Delta}u\|_{L^{2}(\R^{d})}=\|u\|_{L^{2}(\R^{d})}\end{align*}
プランシュレルの等式と$\abs{e^{-it|\xi|^2}}=1$より,
\begin{align*}\|e^{it\Delta}u\|_{L^{2}(\R^{d})}&=\nor{\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}\hat{u}(\xi)}(x)}_{L^{2}(\R^{d})}
\\&=\nor{e^{-it|\xi|^2}\hat{u}(\xi)}_{L^{2}(\R^{d})}
\\&=\nor{\hat{u}(\xi)}_{L^{2}(\R^{d})}=\|u\|_{L^{2}(\R^{d})}\end{align*}
が従う.
上述したようにシュレディンガー方程式の基本解は$|t|$が増大するにつれて一様に0に近付きますが,$L^2$等長性から解の$L^2$ノルムは$t$によらず一定です.
すなわち,解は「消えて」いるわけではなく,空間上で「分散」しているだけであることが分かります.
このことから,$L^{\infty}L^{1}$評価と$L^2$等長性から得られる$L^pL^q$評価は「分散型評価」とも呼ばれるわけですね.
リース-トーリンの複素補間定理
ここで,リース-トーリンの複素補間定理をこの記事で使う形で確認しておきましょう.
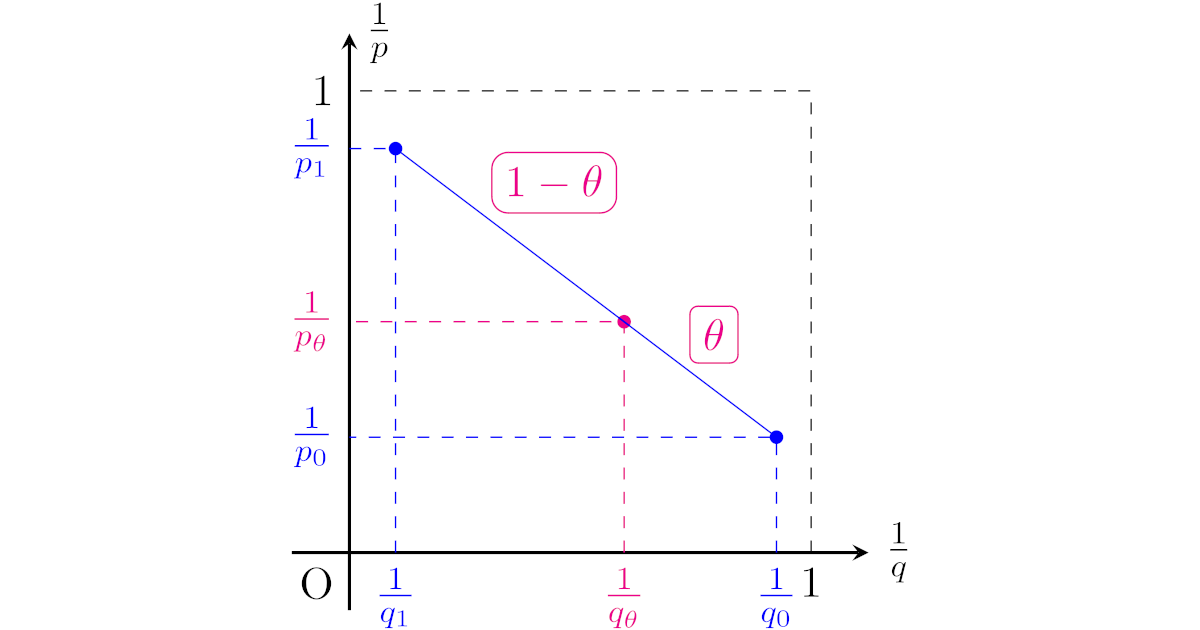
[リース-トーリンの補間定理]$p_0,q_0,p_1,q_1\in[1,\infty]$とする.ある$M_0,M_1>0$が存在して,作用素$T$は
\begin{align*}&\|Tf\|_{L^{p_0}(\R^d)}\le M_0\|f\|_{L^{q_0}(\R^d)}\quad(f\in L^{q_0}(\R^d)),
\\&\|Tf\|_{L^{p_1}(\R^d)}\le M_1\|f\|_{L^{q_1}(\R^d)}\quad(f\in L^{q_1}(\R^d))\end{align*}
を満たすとする.このとき,任意の$\theta\in(0,1)$に対して,$p$, $q$を
\begin{align*}\frac{1}{p}:=\frac{1-\theta}{q_0}+\frac{\theta}{q_1},\quad
\frac{1}{p}:=\frac{1-\theta}{p_0}+\frac{\theta}{p_1}\end{align*}
と定めると,ある$M>0$が存在して
\begin{align*}\|Tf\|_{L^{p}(\R^d)}\le M\|f\|_{L^{q}(\R^d)}\quad(f\in L^{q}(\R^d))\end{align*}
が成り立ち,$M\le M_0^{1-\theta}M_1^{\theta}$が成り立つ.
一般にノルム空間$\mathcal{X},\mathcal{Y}$,作用素$T:\mathcal{X}\to\mathcal{Y}$に対して,ある$K>0$が存在して
\begin{align*}\|Tf\|_{\mathcal{Y}}\le K\|f\|_{\mathcal{X}}\quad(f\in\mathcal{X})\end{align*}
を満たすとき,この$K$の最小値を$f$の作用素ノルムといい,$\|T\|_{\mathcal{X}\to\mathcal{Y}}$などと表します.
いまのリース-トーリンの複素補間定理は
- 作用素$T$は$L^{q_0}(\R^d)$から$L^{p_0}(\R^d)$への有界作用素で$\|T\|_{L^{q_0}(\R^d)\to L^{p_0}(\R^d)}\le M_0$
- 作用素$T$は$L^{q_1}(\R^d)$から$L^{p_1}(\R^d)$への有界作用素で$\|T\|_{L^{q_1}(\R^d)\to L^{p_1}(\R^d)}\le M_1$
を満たせば,$T$は$L^{q}(\R^d)$から$L^{p}(\R^d)$への有界作用素で$\|T\|_{L^{q}(\R^d)\to L^{p}(\R^d)}\le M_0^{1-\theta}M_1^{\theta}$とも言えますね.
リース-トーリンの補間定理の証明は以下の記事を参照してください.
$L^pL^q$評価の証明
以上の準備をもとに,リース-トーリンの複素補間定理から$L^{p}L^{q}$評価を証明しましょう.
[$L^{p}L^{q}$評価(再掲)]$p\in[2,\infty]$と$u\in L^{q}(\R^{d})$に対して
\begin{align*}\|e^{it\Delta}u\|_{L^{p}(\R^{d})}
\le\bra{4\pi|t|}^{-d(\frac{1}{2}-\frac{1}{p})}\|u\|_{L^{q}(\R^{d})}\end{align*}
が成り立つ.ただし,$q\in[1,2]$は$p$のHölder共役である:$1=\frac{1}{p}+\frac{1}{q}$.
$(p,q)=(\infty,1)$の場合($L^{\infty}L^{1}$評価)と$(p,q)=(2,2)$の場合($L^2$等長性)はすでに示した:
- $\|e^{it\Delta}u\|_{\infty}\le\bra{4\pi|t|}^{-\frac{d}{2}}\|u\|_1$
- $\|e^{it\Delta}u\|_2=\|u\|_2$
ここで,座標平面上の2点$\mrm{P_1}(\frac{1}{1},\frac{1}{\infty})=(1,0)$, $\mrm{P_2}(\frac{1}{2},\frac{1}{2})$を考え,線分$\mrm{P_1P_2}$を$\theta:(1-\theta)$ ($\theta\in[0,1]$)に内分する点を$\mrm{P}(\frac{1}{q},\frac{1}{p})$とする.
このとき,リース-トーリンの複素補間定理を用いて
\begin{align*}\|e^{it\Delta}\|_{L^q(\R^{d})\to L^p(\R^{d})}
&\le\brb{\bra{4\pi|t|}^{-\frac{d}{2}}}^{1-\theta}1^{\theta}
\\&=\bra{4\pi|t|}^{-\frac{d}{2}(1-\theta)}\end{align*}
が成り立つ.いま
\begin{align*}&\bmat{1/q\\1/p}=(1-\theta)\bmat{1\\0}+\theta\bmat{1/2\\1/2}\end{align*}
だから,$1=\frac{1}{p}+\frac{1}{q}$であり,$\theta\in[0,1]$より$p$は$p\in[2,\infty]$をくまなく動く.
以上より,任意の$p\in[2,\infty]$に対して
\begin{align*}\|e^{it\Delta}u\|_{p}\le\bra{4\pi|t|}^{-d(\frac{1}{2}-\frac{1}{p})}\|u\|_{q}\end{align*}
が成り立つ.
次の記事では,いま証明した$L^pL^q$評価を用いてストリッカーツ評価を証明します.

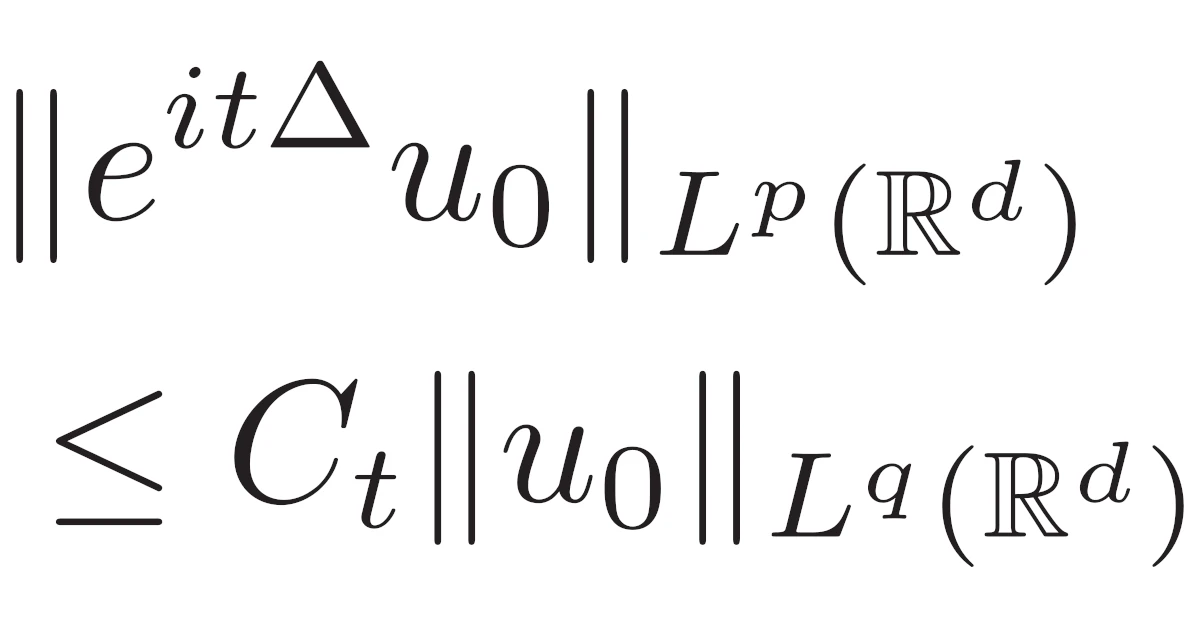
コメント