例えば,空間$d$次元の線形シュレディンガー(Schrödinger)方程式$i\partial_{t}u+\Delta{u}=0$の解$u=e^{it\Delta}f$($f\in\mathcal{S}$)について,時間減衰評価(分散型評価)
\begin{align*}\|e^{it\Delta}f\|_{p}\le C|t|^{-d(\frac{1}{2}-\frac{1}{p})}\|f\|_{p’}\quad(p\ge2)\end{align*}
が成り立ちます.
このような発展方程式(時間発展する偏微分方程式)の解の時間減衰は,解の振る舞いを考察する上で重要となることは多いです.
さて,いまのシュレディンガー発展作用素$e^{it\Delta}$の時間減衰評価は,
\begin{align*}e^{it\Delta}f(x)=\frac{1}{(4\pi it)^{d/2}}\int_{\R^d}e^{-\frac{|x-y|^2}{4it}}f(y)\,dy\end{align*}
と$e^{it\Delta}f(x)$が表せることから得られますが,一般の線形発展方程式においては解が明示的に表せるとは限らずそう単純でないこともよくあります.
そのような明示的な表示ができない場合に,発展作用素の時間減衰評価を求める方法として停留位相法(stationary phase method)があります.
この記事では
- 停留位相法の考え方
- 1次元の停留位相法の計算
- 時間減衰評価の具体例($e^{i(\Delta^2-\Delta)t}$)
を解説します.
停留位相法の考え方
関数$\phi:\R\to\R$に対して微分作用素$e^{it\phi(i|\nabla|)}$は
\begin{align*}e^{it\phi(i|\nabla|)}f=\mathcal{F}^{-1}[e^{it\phi(|\xi|)}\hat{f}]\end{align*}
で定義されます.例えば,微分作用素$e^{it(\Delta^2-\Delta)}$は
\begin{align*}e^{it(\Delta^2-\Delta)}f=&e^{it(i|\nabla|)^2((i|\nabla|)^2+1)}f
\\=&\mathcal{F}^{-1}[e^{it|\xi|^2(|\xi|^2+1)}\hat{f}]\end{align*}
ということになりますね.
微分作用素$e^{it\phi(i|\nabla|)}$の位相関数$\Phi$
微分作用素$e^{it\phi(i|\nabla|)}$に対して,$\Phi(\xi)=\xi\cdot x+t\phi(i|\xi|)$とおくと,関数$f:\R^d\to\R$に対して$e^{t\phi(i|\nabla|)}f$は
\begin{align*}e^{it\phi(i|\nabla|)}f&=\frac{1}{(2\pi)^{d/2}}\int_{\R^d}e^{i\xi\cdot x+it\phi(|\xi|)}\hat{f}(\xi)\,d\xi
\\&=\frac{1}{(2\pi)^{d/2}}\int_{\R^d}e^{i\Phi(\xi)}\hat{f}(\xi)\,d\xi\end{align*}
となります.被積分関数の$e^{i\Phi(\xi)}$が回転を表すので$\Phi$は位相関数(phase function)と呼ばれます.
例えば,$e^{it(\Delta^2-\Delta)}f$の位相関数$\Phi$は
\begin{align*}e^{it(\Delta^2-\Delta)}f=&\frac{1}{(2\pi)^{d/2}}\int_{\R^d}e^{i\xi\cdot x+it|\xi|^2(|\xi|^2+1)}\hat{f}(\xi)\,d\xi\end{align*}
より$\Phi(\xi)=\xi\cdot x+t|\xi|^2(|\xi|^2+1)$ですね.
$\phi$を位相関数ということもあります.
位相関数$\Phi$の停留点
簡単のため$d=1$で$e^{t\phi(i|\nabla|)}f$を考えましょう.集合$A\subset\R_{\xi}$上で$\Phi'(\xi)\neq0$とすると,部分積分により
\begin{align*}\int_{A}e^{i\Phi(\xi)}\hat{f}(\xi)\,d\xi
=&\int_{A}\frac{1}{it\Phi'(\xi)}(e^{it\Phi(\xi)})’\hat{f}(\xi)\,d\xi
\\=&\frac{1}{t}\int_{A}e^{it\Phi(|\xi|)}\bra{\frac{1}{i\Phi'(\xi)}\hat{f}(\xi)}’\,d\xi\end{align*}
となって,時間減衰$\frac{1}{t}$が得られます.
この部分積分を繰り返せば無限に時間減衰が得られることになりますね.
一方,$\Phi'(\eta)=0$となる点$\eta$においては,分母に$0$がくることになるので同様に部分積分をすることはできず,点$\eta$の近傍では区間$[\eta-\epsilon,\eta+\epsilon]$を小さく絞って評価します.
しかし,絞りすぎると分母の$\Phi'(\xi)$が0に近くなってしまうので,$\epsilon$をちょうど良いバランスに設定することで適切な減衰を得ることができます,
このように位相関数$\Phi$について$\phi$が停留する点がポイントとなるので停留位相法と呼ばれるわけですね.
1次元の停留位相法の計算
停留位相法の本質にはファン・デル・コルプトの補題があります.
ファン・デル・コルプトの補題のための補題
まずは次の補題を証明しておきます.
$a<b$なる$a,b\in\R$を考える.$\phi\in C^1([a,b])$が2回微分可能で,任意の$\xi\in[a,b]$に対して
- $\phi'(\xi)\neq0$
- $\phi^{\prime\prime}(\xi)\ge0$または$\phi^{\prime\prime}(\xi)\le0$(すなわち単調)
を同時に満たすとき,$t\neq0$において
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}\,d\xi}\le\frac{2}{|t|}\bra{\frac{1}{|\phi'(b)|}-\frac{1}{|\phi'(a)|}}\end{align*}
が成り立つ.
部分積分により
\begin{align*}\int_{a}^{b}e^{it\phi(\xi)}\,d\xi
=&\frac{1}{it}\int_{a}^{b}\frac{(e^{it\phi(\xi)})’}{\phi'(\xi)}\,d\xi
\\=&\frac{1}{it}\bra{\brc{\frac{e^{it\phi(\xi)}}{\phi'(\xi)}}_{a}^{b}-\int_{a}^{b}\bra{\frac{1}{\phi'(\xi)}}’e^{it\phi(\xi)}\,d\xi}
\\=&\frac{1}{it}\bra{\frac{e^{it\phi(b)}}{\phi'(b)}-\frac{e^{it\phi(a)}}{\phi'(a)}+\int_{a}^{b}\frac{\phi^{\prime\prime}(\xi)e^{it\phi(\xi)}}{\phi'(\xi)^2}\,d\xi}\end{align*}
である.よって,$[a,b]$上で$\phi^{\prime\prime}\ge0$なら,三角不等式と併せて
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}\,d\xi}
\le&\frac{1}{|t|}\bra{\frac{1}{|\phi'(b)|}+\frac{1}{|\phi'(a)|}+\int_{a}^{b}\frac{\phi^{\prime\prime}(\xi)}{\phi'(\xi)^2}\,d\xi}
\\=&\frac{1}{|t|}\bra{\frac{1}{|\phi'(b)|}+\frac{1}{|\phi'(a)|}+\brc{\frac{1}{\phi'(\xi)}}_{a}^{b}}\quad\dots(*)
\\\le&\frac{2}{|t|}\bra{\frac{1}{|\phi'(b)|}+\frac{1}{|\phi'(a)|}}\end{align*}
を得る.一方,$[a,b]$上で$\phi^{\prime\prime}\le0$なら$(*)$の最後の項の符号が$-$に変わるだけなので,同じ結果が得られる.
ファン・デル・コルプトの補題
次の定理をファン・デル・コルプト(van der Corput)の補題といいます.
$a<b$なる$a,b\in\R$を考える.$[a,b]$上の関数$\phi$はある$k\in\N$が存在して$\phi\in C^k([a,b])$を満たすとする.
- $k=1$のとき,2回微分可能で$|\phi'(\xi)|\ge1$かつ$[a,b]$上で$\phi’$が単調
- $k\ge2$のとき,$|\phi^{(k)}(\xi)|\ge1$
であれば,ある定数$C_k>0$が存在して
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}\,d\xi}\le C_k|t|^{-1/k}\end{align*}
が成り立つ.
数学的帰納法により示す.
[1]$k=1$のときに成り立つことを示す.
$\phi’$が単調であることから,$\phi^{\prime\prime}(\xi)\ge0$または$\phi^{\prime\prime}(\xi)\le0$が成り立つから,上の補題により成り立つ.
[2]ある$k$で成り立つと仮定し,$k+1$で成り立つことを示す.
$\phi\in C^{k+1}([a,b])$なら$\phi^{(k+1)}$は連続だから,$\phi^{(k+1)}\ge1$または$\phi^{(k+1)}\le-1$が成り立つ.いずれの場合も$\phi^{(k)}$は単調だから,$\phi^{(k)}$の零点は存在しても1つしかない.
$\phi^{(k)}$が零点をもたない場合は(この記事の「停留位相法」の考え方で説明したように)部分積分により$|t|^{-1}$の減衰が得られ補題は成り立つから,以下では$\phi^{(k)}$が零点$\eta$をもつ場合を考える:$\phi'(\eta)=0$.
$\phi^{(k+1)}\ge1$, $\phi^{(k+1)}\le-1$のいずれの場合も,任意の$\epsilon>0$に対して$[a,\eta-\epsilon]\cup[\eta+\epsilon,b]$上で
\begin{align*}|\phi^{(k)}|\ge\epsilon
\iff\abs{\frac{\phi^{(k)}}{\epsilon}}\ge1\end{align*}
が成り立つから,帰納法の仮定より
\begin{align*}I:=&\abs{\int_{a}^{\eta-\epsilon}e^{it\phi(\xi)}\,d\xi}
\\=&\abs{\int_{a}^{\eta-\epsilon}e^{i(\epsilon t)\frac{\phi(\xi)}{\epsilon}}\,d\xi}
\le C(\epsilon|t|)^{-1/k}\end{align*}
が成り立ち,同様に
\begin{align*}I\!I:=\abs{\int_{\eta+\epsilon}^{b}e^{it\phi(\xi)}\,d\xi}\le C(\epsilon|t|)^{-1/k}\end{align*}
も成り立つ.さらに
\begin{align*}I\!I\!I:=\abs{\int_{\eta-\epsilon}^{\eta+\epsilon}e^{it\phi(\xi)}\,d\xi}\le\int_{\eta-\epsilon}^{\eta+\epsilon}\,d\xi=2\epsilon\end{align*}
なので,三角不等式から
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}\,d\xi}\le I+I\!I+I\!I\!I\le2C(\epsilon|t|)^{-1/k}+2\epsilon\end{align*}
が成り立つ.ここで,$(\epsilon|t|)^{-1/k}=\epsilon$となる$\epsilon$は$\epsilon=|t|^{\frac{k}{k+1}}$なので,
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}\,d\xi}\le2(C+1)|t|^{-\frac{1}{k+1}}\end{align*}
を得る.
この証明で本質的に重要な部分は
- $I\!I\!I$の積分区間の幅$2\epsilon$を小さくしたい
- $[a,\eta-\epsilon]\cup[\eta+\epsilon,b]$の下限$\epsilon$を大きくしたい
ということから,$(\epsilon|t|)^{-1/k}=\epsilon$によりバランスよく$\epsilon$をとっているところです.つまり,停留位相法は
- 停留点近傍の領域をどれだけ絞るか
- 停留点から少し離れたところで$\phi’$がどれくらい増大しているか
を最適なバランスで考えて時間減衰を得る方法ということができます.
ファン・デル・コルプトの補題の系
いまの定理から得られる次の系をファン・デル・コルプトの補題ということもあります.
$a<b$なる$a,b\in\R$を考える.$[a,b]$上の関数$\phi$はある$k\in\N$が存在して$\phi\in C^k([a,b])$を満たすとする.
- $k=1$のとき,2回微分可能で$|\phi'(\xi)|\ge1$かつ$[a,b]$上で$\phi’$が単調
- $k\ge2$のとき,$|\phi^{(k)}(\xi)|\ge1$
であれば,ある定数$C_k>0$が存在して,$f’\in L^1(a,b)$を満たす1回微分可能な$[a,b]$上の関数$f$に対して,
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}f(\xi)\,d\xi}\le C|t|^{-1/k}(|f(b)|+\|f’\|_{L^1})\end{align*}
が成り立つ.
微分積分学の基本定理と部分積分により
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}f(\xi)\,d\xi}
=&\abs{\int_{a}^{b}\od{}{\xi}\bra{\int_{a}^{\xi}e^{it\phi(\zeta)}\,d\zeta}f(\xi)\,d\xi}
\\=&\abs{f(b)\int_{a}^{b}e^{it\phi(\zeta)}\,d\zeta-\int_{a}^{b}f'(\xi)\bra{\int_{a}^{\xi}e^{it\phi(\zeta)}\,d\zeta}\,d\xi}
\\\le&|f(b)|\abs{\int_{a}^{b}e^{it\phi(\zeta)}\,d\zeta}+\nor{\int_{a}^{\xi}e^{it\phi(\zeta)}\,d\zeta}_{L^\infty}\|f'(\xi)\|_{L^1}\end{align*}
となるから,前定理より
\begin{align*}\abs{\int_{a}^{b}e^{it\phi(\xi)}f(\xi)\,d\xi}
\le C|t|^{-1/k}(|f(b)|+\|f'(\xi)\|_{L^1})\end{align*}
が従う.
停留位相法の具体例($e^{i(\Delta^2-\Delta)t}$)
高次元になるときちんと証明するのは少々面倒ですが,上の定理の証明と同様に考えればおおよその減衰が直感的に得られます.
ここでは具体例として,$d$次元の$e^{i(\Delta^2-\Delta)t}$の時間減衰評価を直感的に導出します.
なお,$e^{i(\Delta^2-\Delta)t}$は例えば量子ザハロフ系(quantum Zakharov system)において現れる発展作用素(のひとつ)です.
$p\in[2,\infty]$とする.$f\in B^{0}_{p’,2}(\R^d)$に対して,
\begin{align*}\|e^{it(\Delta^2-\Delta)}f\|_{B^{0}_{p,2}}\le|t|^{-d(\frac{1}{2}-\frac{1}{p})}\|f\|_{B^{-d(1-\frac{2}{p})}_{p’,2}}\end{align*}
が成り立つ.ただし,$p’$は$p$のHölder共役で,$B^{s}_{p,2}(\R^d)$は非斉次Besov空間である.
埋め込み$L^{p’}\subset B^{0}_{p’,2}$, $B^{0}_{p,2}\subset L^p$により$\|e^{it(\Delta^2-\Delta)}f\|_{L^{p}}\le\|f\|_{L^{p’}}$も成り立ちます,
$p=2,\infty$の場合を示せば,$p\in(2,\infty)$の場合は補間定理により得られます.
$p=2$の場合は$B^{0}_{2,2}=L^2$とPlancherelの定理より
\begin{align*}\|e^{it(\Delta^2-\Delta)}f\|_{B^{0}_{2,2}}
=&\|e^{it(\Delta^2-\Delta)}f\|_{L^{2}}
=\|e^{it|\xi|^2(|\xi|^2+1)}\hat{f}\|_{L_{\xi}^{2}}
\\=&\|\hat{f}\|_{L_{\xi}^{2}}
=\|f\|_{L^{2}}=\|f\|_{B^{0}_{2′,2}}\end{align*}
となって成り立つので,あとは$p=\infty$の場合を考えればよいですね.
以下,$\phi:\R\to\R;r\mapsto r^2(r^2+1)$とおき,このとき
\begin{align*}e^{it(\Delta^2-\Delta)}f=e^{it(-\Delta)(-\Delta+1)}f=e^{it\phi(i|\nabla|)}f\end{align*}
と書けることに注意しましょう.
ステップ1:$\|e^{it\phi(i|\nabla|)}f\|_{B^{0}_{\infty,2}}$の分解
まずは$\|e^{it\phi(i|\nabla|)}f\|_{B^{0}_{\infty,2}}$を時間減衰部分と$\|f\|_{B^{0}_{1,2}}$に分けましょう.
$\{\varphi_{k}\}_{k\in\N_{\ge0}}$をLittlewood-Paleyの2進単位分解とし,$\psi:=1-\sum_{k=1}^{\infty}\varphi_k$とすると
\begin{align*}\|e^{it\phi(i|\nabla|)}f\|_{B^{0}_{\infty,2}}
=&\|\mathcal{F}^{-1}[e^{it\phi(|\cdot|)}\hat{f}]\|_{B^{0}_{\infty,2}}
\\=&\|\psi*\mathcal{F}^{-1}[e^{it\phi(|\cdot|)}\hat{f}]\|_{L^\infty}
\\&+\bra{\sum_{k=1}^{\infty}\|\varphi_k*\mathcal{F}^{-1}[e^{it\phi(|\cdot|)}\hat{f}]\|_{L^{\infty}}^2}^{1/2}\end{align*}
です.また,$\widetilde{\varphi}_k:=\varphi_{k-1}+\varphi_k+\varphi_{k+1}$とおくと$\hat{\varphi}_k=\hat{\widetilde{\varphi}}_k\hat{\varphi}_k$なので,
\begin{align*}\varphi_k*\mathcal{F}^{-1}[e^{it\phi(|\xi|)}\hat{f}]
=&\mathcal{F}^{-1}[\hat{\varphi}_ke^{it\phi(|\xi|)}\hat{f}]
\\=&\mathcal{F}^{-1}[\hat{\widetilde{\varphi}}_k\hat{\varphi}_ke^{it\phi(|\xi|)}\hat{f}]
\\=&\mathcal{F}^{-1}[\hat{\varphi}_ke^{it\phi(|\xi|)}]*\mathcal{F}^{-1}[\hat{\widetilde{\varphi}}_k\hat{f}]\end{align*}
だから,Youngの不等式より
\begin{align*}&\|\varphi_k*\mathcal{F}^{-1}[e^{it\phi(|\cdot|)}\hat{f}]\|_{L^{\infty}}
\\=&\|\mathcal{F}^{-1}[\hat{\varphi}_ke^{it\phi(|\cdot|)}]\|_{L^\infty}\|\mathcal{F}^{-1}[\hat{\widetilde{\varphi}}_k\hat{f}]\|_{L^1}
\\=&\nor{\int_{\R^d}\hat{\varphi}_k(\xi)e^{i\xi\cdot x+it\phi(|\xi|)}\,d\xi}_{L^\infty}\|\widetilde{\varphi}_k*f\|_{L^1}
\\\sim&\nor{\int_{\R^d}\hat{\varphi}_k(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}\|\varphi_k*f\|_{L^1}\end{align*}
が成り立ちます.ただし,最後の等式では$\Phi(\xi):=\xi\cdot x+t\phi(|\xi|)$とおきました.$\psi$については$\widetilde{\varphi}_k$の代わりに$\psi+\varphi_1$を用いれば同様に評価できて,
\begin{align*}\|e^{it\phi(i|\nabla|)}f\|_{B^{0}_{\infty,2}}
\le&\nor{\int_{\R^d}\hat{\psi}(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}\|\psi*f\|_{L^1}
\\&+\bra{\sum_{k=1}^{\infty}\nor{\int_{\R^d}\hat{\varphi}_k(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}^2\|\varphi_k*f\|_{L^1}^2}^{1/2}\end{align*}
となりますね.
よって,あとは
- $\nor{\int_{\R^d}\hat{\psi}(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}$
- $\nor{\int_{\R^d}\hat{\varphi}_k(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}$
の時間減衰評価を考えればよいわけですね.
ステップ2:位相関数$\Phi$の停留点
停留位相法においては位相関数$\Phi$の停留点付近での評価が大切でしたから,$\Phi$の停留点について考えましょう.
$\Phi(\xi)=\xi x+t\phi(|\xi|)$だったので,$\nabla|\xi|=\frac{\xi}{|\xi|}$に注意すると
\begin{align*}\nabla\Phi(\xi)=x+t\phi'(|\xi|)\frac{\xi}{|\xi|}\end{align*}
となります.
$\Phi$の停留点を考える上では$\nabla\Phi$の対称性から$x=|x|\m{e}_1$としても一般性を失わず,このとき$\Phi$の停留点$\eta$が存在するなら$\eta=ce_1$ ($c\in\R$)の形に表せますね.
なお,$c$は$x,t$に依存して決まりますね.
ステップ3:位相関数$\Phi$の停留点でのヘッシアン
停留点$\eta$近くでの$\nabla\Phi$の増大度を調べるために,$\Phi$のヘッシアン$\nabla^2\Phi$の停留点$\eta$での値を考えましょう.
\begin{align*}\nabla^2\Phi(\xi)=&t\bra{\phi^{\prime\prime}(|\xi|)\frac{\xi}{|\xi|}\frac{\xi^T}{|\xi|}+\phi'(|\xi|)\frac{1}{|\xi|}\bra{I-\frac{\xi}{|\xi|}\frac{\xi^T}{|\xi|}}}\end{align*}
と計算できるので,
\begin{align*}\nabla^2\Phi(\eta)=t\bra{\phi^{\prime\prime}(c)e_1e_1^T+\frac{\phi'(c)}{c}(I-e_1e_1^T)}
=t\bmat{\phi^{\prime\prime}(c)&0&\dots&0\\0&\phi'(c)/c&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\phi'(c)/c}\end{align*}
となります.いま$\phi'(r)=2r(2r^2+1)$, $\phi^{\prime\prime}(r)=12r^2+2$なので,
\begin{align*}\nabla^2\Phi(\eta)\sim t\bmat{c^2+1&0&\dots&0\\0&c^2+1&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&c^2+1}\end{align*}
となります.
よって,$\partial_k\Phi$は停留点付近で$\xi_k$軸方向に$c^2+1$程度の増大をしていることが分かりました.
ステップ4:最適な$\epsilon$の決定
これより,停留点$\eta=ce_1$付近の直方体$A:=[c-\epsilon,c+\epsilon]\times[-\epsilon,\epsilon]^{d-1}$ ($\epsilon>0$)を考えると,
\begin{align*}\nor{\int_{A}\hat{\varphi}_k(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}\le|A|=(2\epsilon)^d\end{align*}
です.
一方,$\hat{\varphi}_k$は周波数$2^j$付近のカットオフなので$c\sim2^j$であれば,$A$の境界で$\partial_k\Phi$の$\xi_k$軸方向の下限は$\epsilon(2^{2j}+1)$程度となっています.
よって,$A$の領域の狭さと$A$の境界での下限のバランスを
\begin{align*}(\epsilon|t|(2^{2j}+1))^{-d}=\epsilon^d
\iff\epsilon^d=|t|^{-d/2}(2^{2j}+1)^{-d/2}\end{align*}
でとると,直観的には
\begin{align*}\nor{\int_{\R^n}\hat{\varphi}_k(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}\le C|t|^{-d/2}(2^{2j}+1)^{-d/2}\end{align*}
となり,同様に
\begin{align*}\nor{\int_{\R^n}\hat{\psi}(\xi)e^{i\Phi(\xi)}\,d\xi}_{L^\infty}\le C|t|^{-d/2}\end{align*}
となることが分かります.
いまの議論では停留点付近でしか考えていないので,きちんと示すには停留点から離れたところでもこの評価が得られることを示す必要があります.
よって,ステップ1と併せて,
\begin{align*}\|e^{it\phi(i|\nabla|)}f\|_{B^{0}_{\infty,2}}
\le&C|t|^{-d/2}\bra{\|\psi*f\|_{L^1}+\bra{\sum_{k=1}^{\infty}(2^{2j}+1)^{-\frac{d}{2}\cdot2}\|\varphi_k*f\|_{L^1}^2}^{1/2}}
\\=&C|t|^{-d/2}\|f\|_{B^{-d}_{1,2}}\end{align*}
が直観的に得られることが分かりますね.

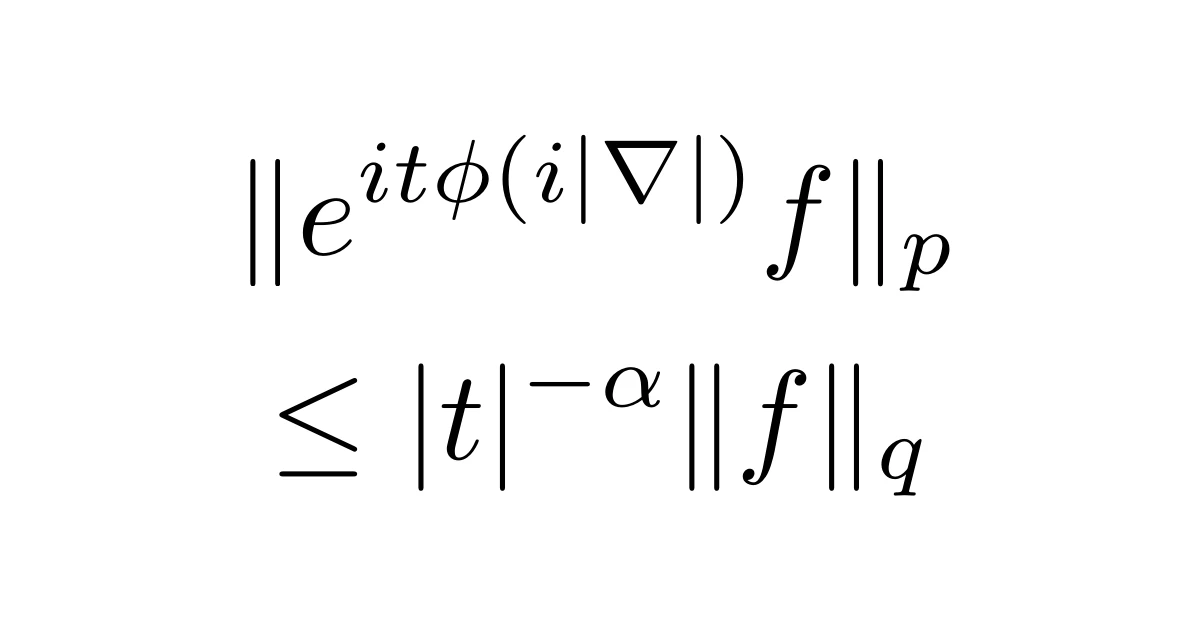
コメント