定数$c,\ell>0$と,$[0,\ell]$上の実数値関数$f$をとり,次の線形熱方程式の初期値・境界値問題を考えます:
\begin{align*}\left\{\begin{aligned}&\frac{\partial u}{\partial t}(x,t)=c\frac{\partial^2u}{\partial x^2}(x,t)&&(0<x<\ell,t>0),\\
&u(0,t)=u(\ell,t)=0&&(t\ge0),\\
&u(x,0)=f(x)&&(0\le x\le \ell).\end{aligned}\right.\end{align*}
この問題の解$u(x,t)$はフーリエ級数展開を用いて表すことができる典型的な例としてよく知られています.
この記事では
- 線形熱方程式の初期値・境界値問題の捉え方
- フーリエ級数を用いた変数分離解の形式的な導出
- 導出した変数分離解が厳密に解となっていることの証明
を順に解説します.
線形熱方程式の初期値・境界値問題の捉え方
熱方程式は熱の伝わり方を記述する偏微分方程式です.まずは直観的に熱方程式の初期値・境界値問題がどう捉えられるかを解説します.
線形熱方程式の捉え方
1次元の線形熱方程式の未知関数$u$は空間変数$x$と時間変数$t$の2変数関数になっており,
\begin{align*}\frac{\partial u}{\partial t}(x,t)=c\frac{\partial^2u}{\partial x^2}(x,t)\quad(*)\end{align*}
と表されます.ここで,「1次元の」とは空間変数$x$が1変数であるという意味です.
$n$次元の線形熱方程式は$\frac{\partial u}{\partial t}(\m{x},t)=c\Delta{u}(\m{x},t)$と表されます.$\Delta$は$\m{x}$に関するラプラシアンです.
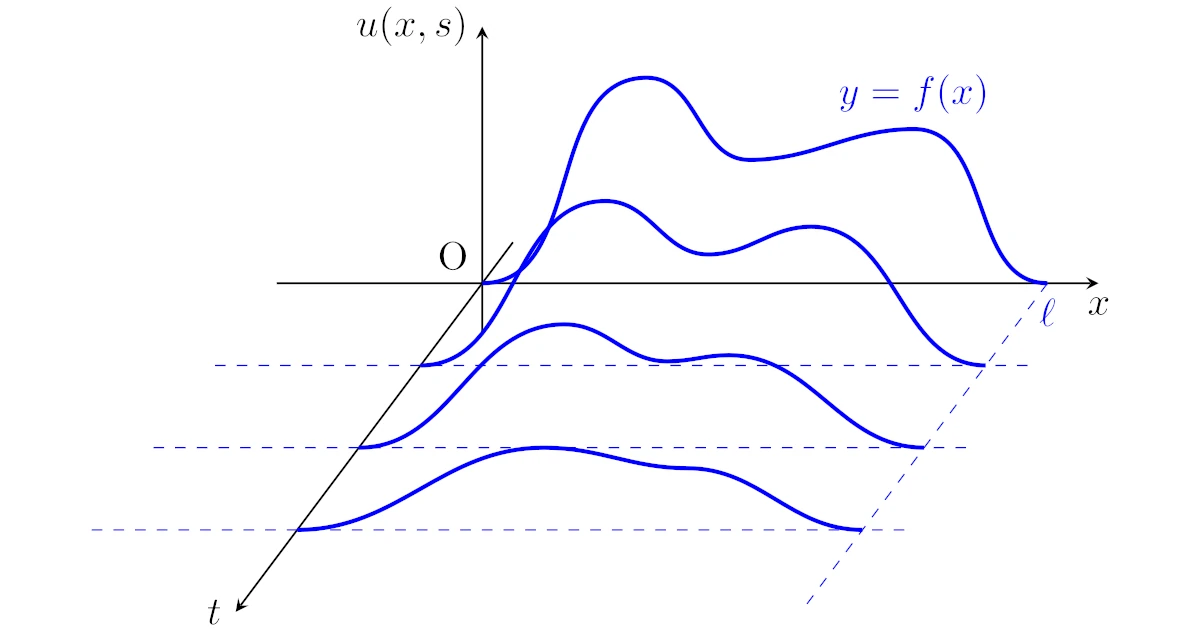
1次元の熱方程式は「まっすぐに伸びた針金の温度$u$が,時間$t$・位置$x$でどうなっているか」と物理的に捉えることができます.
つまり,針金に熱を与えると時間の経過とともに針金の各点の温度が変化していきますから,時刻$t$の針金の位置$x$での温度$u$は$x$と$t$の関数になっていると考えられ,このときの$u$が満たす等式が上の1次元の線形熱方程式$(*)$というわけです.
よって,$u(a,s)$は時刻$t=s$における位置$x=a$の温度を表すわけですね.
2変数らしく$u$のグラフを下図のように表すこともよくあります.時刻$t$軸方向に進むにつれて時間がたった温度の分布になっていますね.
境界値条件の捉え方
今回の熱方程式では$0\le x\le \ell$に制限して考えています.
そこで,空間変数$x$が動く範囲の端点$x=0,\ell$での解$u$の条件を定めておくことがよくあり,この条件を境界値条件といいます.
境界値条件はさまざまなものが考えられますが,この記事で扱う境界値条件
\begin{align*}u(0,t)=u(\ell,t)=0\end{align*}
は端点$x=0,\ell$で$u$は常に0であるという条件ですね.このように,境界での$u(x,t)$の値を与える境界値条件をディリクレ境界条件といいます.
他の境界値としては,境界での$\frac{\partial u}{\partial x}$の値を与えるノイマン境界条件などがあります.
初期条件の捉え方
初期条件はある時刻での解$u$の条件を定めておくことがよくあり,この条件を初期条件といいます.
この記事で扱う初期条件
\begin{align*}u(x,0)=f(x)\end{align*}
は時刻0での解$u$は$f$に等しいという条件ですね.
つまり,時刻0で温度分布が$f(x)$になっているところからスタートして,どのように温度が変化していくかということを考えるわけですね.
よって,初期値・境界値条件も考えた$u$のグラフを描くと下図のようになります.
フーリエ級数を用いた変数分離解の形式的な導出
定数$c,\ell>0$と,$[0,\ell]$上の実数値関数$f$をとります.関数$f$は$[0,\ell]$上連続かつ$(0,\ell)$上区分的$C^1$級であるとしておきます.線形熱方程式の初期値・境界値問題
\begin{align*}\left\{\begin{aligned}&\frac{\partial u}{\partial t}(x,t)=c\frac{\partial^2u}{\partial x^2}(x,t)&&(0<x<\ell,t>0),\\
&u(0,t)=u(\ell,t)=0&&(t\ge0),\\
&u(x,0)=f(x)&&(0\le x\le \ell).\end{aligned}\right.\end{align*}
の解をまずは形式的に求めていきましょう.
「形式的に」とは厳密な正当化はひとまずおいて,概ね成り立ちそうな変形で考えることをいいます.
ステップ1:変数分離解$u(x,t)=v(x)w(t)$の$v$, $w$が満たす微分方程式
変数分離解とは$u(x,t)=(\text{$x$の式})\times(\text{$t$の式})$の形をした解のことをいいます.
今はまだ変数分離解が実際に存在するかどうか分かりませんが,変数分離解$u(x,t)=v(x)w(t)\not\equiv0$が存在するなら,どのような条件を満たすのかを考えていきましょう.
熱方程式$\frac{\partial u}{\partial t}(x,t)=c\frac{\partial^2u}{\partial x^2}(x,t)$に代入すると
\begin{align*}v(x)w^{\prime}(t)=cv^{\prime\prime}(x)w(t)\end{align*}
となり,$v(x)\neq0$, $w(t)\neq0$なら
\begin{align*}\frac{w^{\prime}(t)}{cw(t)}=\frac{v^{\prime\prime}(x)}{v(x)}\end{align*}
が成り立ちます.ここで,右辺は$t$によらず,左辺は$x$によらないので,実は両辺とも$t$にも$x$にもよらないことが分かります.
そこで,この値を定数$-k$とおくと,2つの常微分方程式
\begin{align*}w^{\prime}(t)=-ckw(t),\quad
v^{\prime\prime}(x)=-kv(x)\end{align*}
が得られますね.
のちに$k>0$となることが証明できるので,あえて$-k$とおいています.
ステップ2:$v$, $w$の常微分方程式を解く
ステップ1で得られた常微分方程式はいずれも定数係数斉次線形なので解くことができますね.
まずは$v$の常微分方程式$v^{\prime\prime}(x)=-kv(x)$を解きますが,境界値条件より$v(0)=v(\ell)=0$であることに注意しましょう.
- $k=0$のときは両辺を2回積分して$v(x)=C_1+C_2x$となります.
- $k\neq0$のときは特性方程式が$\lambda^2=-k$で
- $k<0$なら解$\lambda=\pm\sqrt{-k}$は実数なので,解は$v(x)=C_1e^{\sqrt{-k}x}+C_2e^{-\sqrt{-k}x}$
- $k>0$なら解$\lambda=\pm\sqrt{k}i$は虚数なので,解は$v(x)=C_1\sin(\sqrt{k}x)+C_2\cos(\sqrt{k}x)$
となります($C_1$, $C_2$は任意定数).
しかし,$k<0$のときと$k=0$のときは,いずれも$v(0)=v(\ell)=0$を満たすには$C_1=C_2=0$とするしかなく,$v(x)\equiv0$となって最初の仮定$u(x,t)=v(x)w(t)\not\equiv0$に反します.よって,$k>0$であり
\begin{align*}v(x)=C_1\sin(\sqrt{k}x)+C_2\cos(\sqrt{k}x)\end{align*}
となります.
一方,$w$の常微分方程式$w^{\prime}(t)=-ckw(t)$は$w(t)=De^{-ckt}$と解けますね($D$は任意定数).
ステップ3:境界値条件から定数$k>0$を求める
ステップ2で得られた$v(x)$と境界値条件$v(0)=v(\ell)=0$を併せると
\begin{align*}&C_2=C_1\sin(\sqrt{k}\ell)+C_2\cos(\sqrt{k}\ell)=0\end{align*}
だから$C_2=C_1\sin(\sqrt{k}\ell)=0$が得られます.もし$C_1=0$なら$C_2=0$と併せて$v(x)\equiv0$となり不適だから$C_1\neq0$です.よって,$\sin(\sqrt{k}\ell)=0$が成り立ち,
\begin{align*}\sqrt{k}\ell=n\pi\iff k=\frac{n^2\pi^2}{\ell^2}\end{align*}
と表せますね($n\in\N$).
ステップ4:解$u$の形を求める
$k_n:=\frac{n^2\pi^2}{\ell^2}$とおき,$k=k_n$のときの$v$, $w$の常微分方程式の解をそれぞれ$v_n$, $w_n$とすれば,ステップ2で求めたように
\begin{align*}&v_n(x)=p_n\sin(\sqrt{k_n}x)=p_n\sin\bra{\frac{n\pi x}{\ell}},
\\&w_n(t)=q_ne^{-ck_nt}=q_n e^{-cn^2\pi^2t/\ell^2}\end{align*}
と表せます.$a_n=p_nq_n$とおくと,これらの積
\begin{align*}u_n(x,t):=v_n(x)w_n(t)=a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}\end{align*}
はもとの熱方程式の境界値条件を満たす解になっていそうですね.
よって,線形微分方程式の重ね合わせの原理より
\begin{align*}u(x,t)=\sum_{n=1}^{\infty}u_n(x,t)=\sum_{n=1}^{\infty}a_ne^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}\end{align*}
も線形熱方程式の解になり,各$u_n$が$u_n(0)=u_n(\ell)=0$を満たしていることから$u$も$u(0)=u(\ell)=0$を満たしていそうですね.
ステップ5:初期条件から係数$a_n$を求める
最後に$a_n$をうまく選ぶことで初期条件を満たすようにしましょう.ステップ4で得られた関数$u$で初期条件$u(x,0)=f(x)$を考えると,
\begin{align*}\sum_{n=1}^{\infty}a_n\sin\bra{\frac{n\pi x}{\ell}}=f(x)\end{align*}
となります.ここで,次のフーリエ正弦級数展開の定理を確認しておきましょう.
$[0,\ell]$上の$f(0)=0$を満たす関数$f$が,$[0,\ell]$上連続かつ$(0,\ell)$上区分的$C^1$級であれば,$f$のフーリエ正弦級数展開は$[0,\ell]$上で$f$に一様収束する:
\begin{align*}f(x)&=\sum_{n=1}^{\infty}a_n\sin\bra{\frac{n\pi x}{\ell}}
\\&\bra{a_n=\frac{2}{\ell}\int_{0}^{\ell}f(x)\sin{\bra{\frac{n\pi x}{\ell}}}\,dx}\end{align*}
一般に,区分的$C^1$級であれば$f$の連続点で$f$に各点収束し,ここに$f$の連続性が加わると一様収束まで成り立ちます.
関数$f$は$[0,\ell]$上連続かつ$(0,\ell)$上区分的$C^1$級としていたので,この定理が適用できます.左辺は$[0,\ell]$上の$f$のフーリエ正弦級数展開になっていると考えて
\begin{align*}a_n=\frac{2}{\ell}\int_{0}^{\ell}f(x)\sin{\bra{\frac{n\pi x}{\ell}}}\,dx\end{align*}
とおけば良いですね.
導出した変数分離解が厳密に解となっていることの証明
以上より,定数$c,\ell>0$と,$[0,\ell]$上連続かつ$(0,\ell)$上区分的$C^1$級な関数$f$に対して,線形熱方程式の初期値・境界値問題
\begin{align*}\left\{\begin{aligned}&\frac{\partial u}{\partial t}(x,t)=c\frac{\partial^2u}{\partial x^2}(x,t)&&(0<x<\ell,t>0),\\
&u(0,t)=u(\ell,t)=0&&(t\ge0),\\
&u(x,0)=f(x)&&(0\le x\le \ell).\end{aligned}\right.\end{align*}
の解と思しき関数
\begin{align*}u(x,t)=\sum_{n=1}^{\infty}a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}&
\\\bra{a_n=\frac{2}{\ell}\int_{0}^{\ell}f(x)\sin{\bra{\frac{n\pi x}{\ell}}}\,dx}&\end{align*}
を見つけることができました.しかし,細かいことを気にしない形式的な変形だったので,これが厳密に解になっているとはまだ言い切れません.
そこで,最後にこの関数$u$が(適切な関数$f$に対して)確かに解になっていることを証明しましょう.
$u$が項別微分可能なら解となっていることの確認
上で定めた関数
\begin{align*}u(x,t)=\sum_{n=1}^{\infty}a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}&
\\\bra{a_n=\frac{2}{\ell}\int_{0}^{\ell}f(x)\sin{\bra{\frac{n\pi x}{\ell}}}\,dx}&\end{align*}
が項別微分可能であると仮定して,線形熱方程式の初期値・境界値問題の解であることを確認しましょう.
$u$が項別微分可能なので,
\begin{align*}\frac{\partial u}{\partial t}(x,t)&=\sum_{n=1}^{\infty}a_n\bra{-\frac{cn^2\pi^2}{\ell^2}}e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}
\\&=c\sum_{n=1}^{\infty}a_n e^{-cn^2\pi^2t/\ell^2}\bra{\frac{n\pi}{\ell}}^2\bra{-\sin\bra{\frac{n\pi x}{\ell}}}
=c\frac{\partial^2u}{\partial x^2}(x,t)\end{align*}
となって,熱方程式を満たします.
また,$\sin\bra{\frac{n\pi 0}{\ell}}=\sin\bra{\frac{n\pi \ell}{\ell}}=0$なので境界値条件$u(0,t)=u(\ell,t)=0$を満たし,
\begin{align*}u(x,0)=\sum_{n=1}^{\infty}a_n\sin\bra{\frac{n\pi x}{\ell}}\end{align*}
は$a_n$の定義と併せて$f$の$[0,\ell]$上のフーリエ正弦級数展開だから$f(x)$に等しいです.
よって,$u$が項別微分可能なら線形熱方程式の初期値・境界値問題の解であることが分かりました.
$u$が項別微分可能であることの証明
あとは$u$が項別微分可能であることを示せば,厳密に解になっていることが証明されたことになりますね.
項別微分可能であることを証明するために,次の定理を使いましょう.
開区間$I$上の微分可能な実数値関数列$\{f_n\}$に対して,任意の$x\in I$に対して$\sum_{n=1}^{\infty}f_n(x)$は収束するとする.このとき,
- $\forall x\in I\quad|{f_n}'(x)|\le M_n$
- $\sum_{n=1}^{\infty}M_n<\infty$
を満たす実数列$\{M_n\}$が存在すれば,$\sum_{n=1}^{\infty}f_n$は$I$上項別微分可能である:
\begin{align*}\bra{\sum_{n=1}^{\infty}f_n}’=\sum_{n=1}^{\infty}{f_n}’.\end{align*}
この定理は数え上げ測度についてルベーグの収束定理を適用することで証明できる項別微分定理で,微分積分学で学ぶものより少し扱いやすいものになっています.
この定理を用いて$(0,\ell)\times(0,\infty)$上で
\begin{align*}u(x,t)=\sum_{n=1}^{\infty}a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}&
\\\bra{a_n=\frac{2}{\ell}\int_{0}^{\ell}f(x)\sin{\bra{\frac{n\pi x}{\ell}}}\,dx}&\end{align*}
が項別微分可能であることを示しましょう.以下では,$f$のフーリエ係数の性質として
- フーリエ係数の数列$\{a_n\}$は絶対収束する:$\sum\limits_{n=1}^{\infty}|a_n|<\infty$
- ある$M>0$が存在して$|a_n|<M$が成り立つ
ことを用います.まず,任意の$(x,t)\in(0,\ell)\times(0,\infty)$に対して,
\begin{align*}\sum_{n=1}^{\infty}\abs{a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}}\le\sum_{n=1}^{\infty}|a_n|<\infty\end{align*}
と$u(x,t)$は絶対収束するので,$u(x,t)$は収束します.
$u$が$x$について項別微分可能であることの証明
任意に$t\in(0,\infty)$をとります.各$a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}$は$x$について$(0,\ell)$上微分可能であり,任意の$x\in(0,\ell)$に対して
\begin{align*}\abs{\frac{\partial}{\partial x}\bra{a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}}}
&=\abs{\frac{n\pi a_n}{\ell} e^{-cn^2\pi^2t/\ell^2}\cos\bra{\frac{n\pi x}{\ell}}}
\\&\le\frac{n\pi |a_n|}{\ell}e^{-cn^2\pi^2t/\ell^2}\end{align*}
が成り立ちます.また,この最右辺の級数は
\begin{align*}\sum_{n=1}^{\infty}\frac{n\pi |a_n|}{\ell}e^{-cn^2\pi^2t/\ell^2}
\le\frac{\pi M}{\ell}\sum_{n=1}^{\infty}ne^{-cn^2\pi^2t/\ell^2}<\infty\end{align*}
と収束するので,項別微分定理が適用できて$u$は$x$について項別微分可能で
\begin{align*}\frac{\partial u}{\partial x}(x,t)=\frac{n\pi a_n}{\ell} e^{-cn^2\pi^2t/\ell^2}\cos\bra{\frac{n\pi x}{\ell}}\end{align*}
が成り立ちます.
$\frac{\partial u}{\partial x}$が$x$について項別微分可能であることの証明
$u$が$x$について項別微分可能であることの証明と流れは同じですが,細かいところは少し変わるので念の為示しておきましょう.
任意に$t\in(0,\infty)$をとります.各$\frac{n\pi a_n}{\ell}e^{-cn^2\pi^2t/\ell^2}\cos\bra{\frac{n\pi x}{\ell}}$は$x$について$(0,\ell)$上微分可能であり,任意の$x\in(0,\ell)$に対して
\begin{align*}\abs{\frac{\partial}{\partial x}\bra{\frac{n\pi a_n}{\ell}e^{-cn^2\pi^2t/\ell^2}\cos\bra{\frac{n\pi x}{\ell}}}}
&=\abs{-\frac{n^2\pi^2 a_n}{\ell^2} e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}}
\\&\le\frac{n^2\pi^2 |a_n|}{\ell^2}e^{-cn^2\pi^2t/\ell^2}\end{align*}
が成り立ちます.また,この最右辺の級数は
\begin{align*}&\sum_{n=1}^{\infty}\frac{n^2\pi^2 |a_n|}{\ell^2}e^{-cn^2\pi^2t/\ell^2}
\le\frac{\pi^2 M}{\ell^2}\sum_{n=1}^{\infty}n^2e^{-cn^2\pi^2t/\ell^2}<\infty\end{align*}
と収束するので,項別微分定理が適用できて$\frac{\partial u}{\partial x}$は$x$について項別微分可能で
\begin{align*}\frac{\partial^2 u}{\partial x^2}(x,s)=-\frac{n^2\pi^2 a_n}{\ell^2} e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi x}{\ell}}\end{align*}
が成り立ちます.
$u$が$t$について項別微分可能であることの証明
任意に$\delta>0$を固定します.$(0,\ell)\times(\delta,\infty)$上で項別微分可能であることを示せば,$\delta$の任意性より$(0,\ell)\times(0,\infty)$上で項別微分可能であることが従いますね.
任意に$x\in(0,\ell)$をとります.各$a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi a}{\ell}}$は$t$について$(\delta,\infty)$上微分可能であり,任意の$t\in(\delta,\infty)$に対して
\begin{align*}\abs{\frac{\partial}{\partial t}\bra{a_n e^{-cn^2\pi^2t/\ell^2}\sin\bra{\frac{n\pi a}{\ell}}}}
&=\abs{-\frac{cn^2\pi^2 a_n}{\ell^2}e^{-cn^2\pi^2t/\ell^2}\cos\bra{\frac{n\pi a}{\ell}}}
\\&\le\frac{cn^2\pi^2|a_n|}{\ell^2}e^{-cn^2\pi^2\delta/\ell^2}\end{align*}
が成り立ちます.また,この最右辺の級数は
\begin{align*}sum_{n=1}^{\infty}\frac{cn^2\pi^2|a_n|}{\ell^2}e^{-cn^2\pi^2\delta/\ell^2}
\le\frac{c\pi^2M}{\ell^2}\sum_{n=1}^{\infty}n^2e^{-cn^2\pi^2\delta/\ell^2}<\infty\end{align*}
と収束するので,項別微分定理が適用できて$u$は$t$について項別微分可能で
\begin{align*}\frac{\partial u}{\partial t}(a,t)=-\frac{cn^2\pi^2 a_n}{\ell^2}e^{-cn^2\pi^2t/\ell^2}\cos\bra{\frac{n\pi a}{\ell}}\end{align*}
が成り立ちます.

コメント