確率変数列$\{X_n\}_{n\in\N}$の収束として,
- 概収束$X_n\to X\ \text{a.s.}$
- $p$次平均収束$X_n\xrightarrow[]{L^p}X$
- 確率収束$X_n\xrightarrow[]{P}X$
- 分布収束(法則収束)$X_n\xrightarrow[]{L}X$
の4種類が基本的で広く用いられています.
また,これらの収束は無関係ではなく「概収束すれば確率収束」「$p$次平均収束すれば確率収束」「確率収束すれば分布収束(法則収束)」という関係があります.
この記事では
- 参考文献
- 確率変数の4つの収束(概収束・平均収束・確率収束・分布収束)
- 概収束・平均収束・確率収束・分布収束の強さの順
- 4つの収束をする例としない例
を順に解説します.
一連の記事はこちら
【確率変数の4つの収束|概収束,平均収束,確率収束,分布収束】←この記事
【一様可積分とヴィタリの収束定理|ルベーグの収束定理の一般化】
【一様可積分性の判定条件|十分条件と必要十分条件】
参考文献
確率論
[舟木直久 著/朝倉書店]
本書は確率論の入門書で,全体を通して丁寧に書かれています.
第1章では確率論の概説がなされており,例えば「大数の弱法則」「大数の強法則」にまで平易な説明で触れられているのが嬉しいです.
ただし,本書の「まえがき」に書かれているように,第2章から第5章は大学3年〜4年相当の確率論の内容となっているので,第2章以降を読むにはそれなりの基礎が必要となります.
第6章,第7章では代表的な確率過程である「マルチンゲール」「マルコフ過程」が解説されています.
本書は全体を通して「なぜその概念を学ぶ必要があるのか」という動機付けが大切にされており,新しい概念を前向きに理解しやすい点が優れている好著となっています.
確率変数の4つの収束(概収束・平均収束・確率収束・分布収束)
まずは確率変数の定義を確認しておきましょう.
$(\Omega,\mathcal{F},\mathbb{P})$を確率空間とし,$(S,\mathcal{S})$を可測空間する.このとき,可測な写像$X:\Omega\to S$を$S$値確率変数(random variable)という.
特に,$S=\R$, $\mathcal{S}=\mathcal{B}(\R)$($\R$上のボレル集合族)の場合,$X$を実数値確率変数(real-valued random variable)という.
例えば,6面サイコロをふることに対応する確率空間$(\Omega,\mathcal{F},\mathbb{P})$は
- $\Omega=\{1,2,3,4,5,6\}$
- $\mathcal{F}=2^\Omega$ ($\Omega$の冪集合)
- $\mathbb{P}(\{\omega\})=\frac{1}{6}$ ($\omega\in\Omega$)
です.サイコロを振って
- 1,2,3の目が出れば10点
- 4,5の目が出れば20点
- 6の目が出れば30点
とサイコロの目に点数を与える状況は
- $S=\{10,20,30\}$
- $\mathcal{S}=2^S$($S$の冪集合)
- $X:\Omega\to S;\begin{cases}1,2,3\mapsto 10\\4,5\mapsto 20\\6\mapsto 30\end{cases}$
なる可測空間$(S,\mathcal{S})$と確率変数$X:\Omega\to S$を定めることによって表現できます.
この記事では$(\Omega,\mathcal{F},\mathbb{P})$を確率空間とし,$\mathbb{E}$で期待値,集合$A\subset\Omega$上の定義関数を$\mathbb{I}_{A}$で表します:
\begin{align*}\mathbb{E}[X]=\int_{\Omega}X(\omega)\,\mathbb{P}(d\omega),\quad
\mathbb{I}_{A}(\omega)=\begin{cases}1,&\omega\in A,\\0,&\omega\notin A.\end{cases}\end{align*}
概収束:$X_n$が確率1で$X$に各点収束
実数値確率変数列$\{X_n\}_{n\in\N}$が確率変数$X$に概収束(almost sure convergence)するとは,
\begin{align*}\mathbb{P}\bra{\set{\omega\in\Omega}{\lim_{n\to\infty}X_n(\omega)=X(\omega)}}=1\end{align*}
を満たすことをいう.このとき,$X_n\to X\ \text{a.s.}$などと表す.
「$\lim\limits_{n\to\infty}X_n(\omega)=X(\omega)$を満たさない$\omega\in\Omega$はいるかもしれないが,そのような$\omega$の確率は0である」というのが概収束の定義の意味です.
この定義は「$n\to\infty$でほとんど確実に$X_n$が$X$に収束する」とも言います.
概収束$X_n\to X\ \text{a.s.}$のa.s.は,almost surely(ほとんど確実に)の略です.
$p$次平均収束:$X_n$と$X$の差の絶対値の$p$乗の期待値が0に収束
$p\in[1,\infty)$に対して実数値確率変数列$\{X_n\}_{n\in\N}$が確率変数$X$に$p$次平均収束(convergence in the mean of order $p$)するとは,
\begin{align*}\lim_{n\to\infty}\mathbb{E}\brc{|X_n-X|^p}=0\end{align*}
を満たすことをいう.このとき,$X_n\xrightarrow[]{L^p}X$などと表す.
実数値確率変数$Y$と$p\in[1,\infty)$に対して,一般に
\begin{align*}\bra{\int_{\Omega}|Y(\omega)|^p\,\mathbb{P}(d\omega)}^{1/p}\end{align*}
を$\|Y\|_{L^p(\Omega)}$で表し$\Omega$上の$L^p$ノルムといいます.$\Omega$上の$L^p$ノルムを用いると,$p$次平均収束の定義式は
\begin{align*}\lim_{n\to\infty}\|X_n-X\|_{L^p(\Omega)}^p=0\end{align*}
と書くこともできますね.
$\|Y\|_{L^p(\Omega)}<\infty$を満たす実数値確率変数$Y$全部の空間$L^p(\Omega)$は$\|\cdot\|_{L^p(\Omega)}$をノルムとしてバナッハ空間となることもよく知られています.
確率収束:$X_n$と$X$が離れている部分の確率が0に収束
実数値確率変数列$\{X_n\}_{n\in\N}$が確率変数$X$に確率収束(stochastic convergence)するとは,任意の$\epsilon>0$に対して,
\begin{align*}\lim_{n\to\infty}\mathbb{P}\bra{\set{\omega\in\Omega}{|X_n(\omega)-X(\omega)|>\epsilon}}=0\end{align*}
を満たすことをいう.このとき,$X_n\xrightarrow[]{P}X$などと表す.
「任意の$\epsilon>0$に対して,『$X_n(\omega)$と$X(\omega)$が$\epsilon$より離れている$\omega\in\Omega$の集合』の確率が,$n$を大きくしていくと0に近付く」というのが確率収束の定義の意味です.
また,この定義式は
\begin{align*}&\lim_{n\to\infty}\int_{\{|X_n-X|>\epsilon\}}\,\mathbb{P}(d\omega)=0,
\\&\lim_{n\to\infty}\mathbb{E}\brc{\mathbb{I}_{\{|X_n-X|>\epsilon\}}}=0\end{align*}
などと表すこともできますね.
正確には
\begin{align*}&\lim_{n\to\infty}\int_{\set{\omega\in\Omega}{|X_n(\omega)-X(\omega)|>\epsilon}}\,\mathbb{P}(d\omega)=0,
\\&\lim_{n\to\infty}\mathbb{E}\brc{\mathbb{I}_{\set{\omega\in\Omega}{|X_n(\omega)-X(\omega)|>\epsilon}}}=0\end{align*}
ですが,添字がかさばると読みにくいため慣習的に上記のように省略して表すことが多いです.
分布収束:$f(X_n)$の期待値が$f(X)$の期待値に収束
実数値確率変数列$\{X_n\}_{n\in\N}$が確率変数$X$に分布収束(convergence in distribution)または法則収束(convergence in law)するとは,任意の実数値有界連続関数$f$に対して
\begin{align*}\lim_{n\to\infty}\mathbb{E}[f(X_n)]=\mathbb{E}[f(X)]\end{align*}
を満たすことをいう.このとき,$X_n\xrightarrow[]{L}X$や$X_n\xrightarrow[]{D}X$などと表す.
$f(x)=\sin{x}$や$f(x)=e^{-x^2}$など任意の実数値有界連続関数$f$に対して成り立つ必要があります.
なお,左辺の期待値と右辺の期待値が別の確率空間によるものであっても構いません.すなわち,
- 確率変数列$\{X_n\}_{n\in\N}$が定義された確率空間
- 確率変数$X$が定義された確率空間
が異なっている場合でも,この定義は問題ありません.
概収束・平均収束・確率収束・分布収束の強さの順
それでは,いまみた4つの収束の強さは
- 概収束 $\Ra$ 確率収束
- $p$次平均収束 $\Ra$ 確率収束
- 確率収束 $\Ra$ 分布収束(法則収束)
となります.このことを証明しましょう.
確率収束がいずれにも関わっていることを意識すると整理しやすいですね.
概収束すれば確率収束する
$\{X_n\}_{n\in\N}$が$X$に概収束するなら,$\{X_n\}_{n\in\N}$は$X$に確率収束する:
\begin{align*}X_n\to X\ \text{a.s.}\quad\Ra\quad X_n\xrightarrow[]{P}X\end{align*}
任意に$\epsilon>0$をとる.$\{X_n\}_{n\in\N}$が$X$に概収束するなら,定義よりほとんど全ての$\omega\in\Omega$に対して
\begin{align*}\lim_{n\to\infty}X_n(\omega)=X(\omega)\end{align*}
だから,ほとんど全ての$\omega\in\Omega$に対して$\lim_{n\to\infty}\mathbb{I}_{\{|X_n-X|>\epsilon\}}(\omega)=0$である.
また,$\Omega$上で$\mathbb{I}_{\{|X_n-X|>\epsilon\}}\le1$であり,$\mathbb{E}(1)=1<\infty$だから,ルベーグの収束定理より
\begin{align*}\lim_{n\to\infty}\mathbb{E}\brc{\mathbb{I}_{\{|X_n-X|>\epsilon\}}}
&=\mathbb{E}\brc{\lim_{n\to\infty}\mathbb{I}_{\{|X_n-X|>\epsilon\}}}
\\&=\mathbb{E}[0]
=0\end{align*}
が従う.すなわち,$\{X_n\}_{n\in\N}$は$X$に確率収束する.
$p$次平均収束すれば確率収束する
任意の$p\in[1,\infty)$に対して$\{X_n\}_{n\in\N}$が$X$に$p$次平均収束するなら,$\{X_n\}_{n\in\N}$は$X$に確率収束する:
\begin{align*}X_n\xrightarrow[]{L^p}X\quad\Ra\quad X_n\xrightarrow[]{P}X\end{align*}
任意の$\epsilon>0$に対して
\begin{align*}0&\le\mathbb{E}\brc{\mathbb{I}_{\{|X_n-X|>\epsilon\}}}
\\&\le\mathbb{E}\brc{\frac{|X_n-X|^p}{\epsilon^p}}
\le\frac{1}{\epsilon^p}\mathbb{E}\brc{|X_n-X|^p}\end{align*}
が成り立つ(本質的にチェビシェフの不等式).
よって,$\{X_n\}_{n\in\N}$が$X$に$p$次平均収束するなら,定義より
\begin{align*}\lim_{n\to\infty}\mathbb{E}\brc{|X_n-X|^p}=0\end{align*}
だから,$\lim\limits_{n\to\infty}\mathbb{E}\brc{\mathbb{I}_{\{|X_n-X|>\epsilon\}}}=0$が従う.すなわち,$\{X_n\}_{n\in\N}$は$X$に確率収束する.
確率収束すれば分布収束する
$\{X_n\}_{n\in\N}$が$X$に確率収束するなら,$\{X_n\}_{n\in\N}$は$X$に分布収束(法則収束)する:
\begin{align*}X_n\xrightarrow[]{P}X\quad\Ra\quad X_n\xrightarrow[]{L}X\end{align*}
任意に$\epsilon>0$,実数値有界連続関数$f$をとり,$M:=\sup\limits_{x\in\R}|f(x)|$とする.
十分大きな$R>0$の設定
一般に
\begin{align*}\lim_{R\to\infty}\mathbb{E}\brc{\mathbb{I}_{\{|X|>R\}}}
=\lim_{R\to\infty}\mathbb{P}(\set{\omega\in\Omega}{|X(\omega)|>R})
=0\end{align*}
なので,ある$R>0$が存在して,
\begin{align*}\mathbb{E}\brc{\mathbb{I}_{\{|X|>R\}}}<\frac{\epsilon}{6M}\end{align*}
が成り立つ.
十分小さな$\delta>0$の設定
有界閉区間$[-2R,2R]$上で$f$は連続だから,$[-2R,2R]$上で$f$は一様連続である(ハイネ-カントールの定理).よって,ある$\delta\in(0,R)$が存在して,$|x-y|\le\delta$かつ$|x|\le R$なら
\begin{align*}|f(x)-f(y)|<\frac{\epsilon}{3}\end{align*}
が成り立つ.
十分大きな$N\in\N$の設定
$\{X_n\}_{n\in\N}$が$X$に確率収束するなら,定義より,ある$N\in\N$が存在して,$n>N$なら
\begin{align*}\mathbb{E}\brc{\mathbb{I}_{\{|X_n-X|>\delta\}}}<\frac{\epsilon}{6M}\end{align*}
が成り立つ.
$|\mathbb{E}[f(X_n)]-\mathbb{E}[f(X)]|$の評価
任意の$n\in\N$に対して,三角不等式より
\begin{align*}|\mathbb{E}[f(X_n)]-\mathbb{E}[f(X)]|\le\mathbb{E}[|f(X_n)-f(X)|],\end{align*}
が成り立ち,
\begin{align*}|f(X_n)-f(X)|
&=|f(X_n)-f(X)|\mathbb{I}_{\{|X|>R\}}
\\&\quad+|f(X_n)-f(X)|\mathbb{I}_{\{|X_n-X|>\delta\}\cap\{|X|\le R\}}
\\&\quad+|f(X_n)-f(X)|\mathbb{I}_{\{|X_n-X|\le\delta\}\cap\{|X|\le R\}}
\\&\le (|f(X_n)|+|f(X)|)\mathbb{I}_{\{|X|>R\}}
\\&\quad+(|f(X_n)|+|f(X)|)\mathbb{I}_{\{|X_n-X|>\delta\}}
\\&\quad+|f(X_n)-f(X)|\mathbb{I}_{\{|X_n-X|\le\delta\}}
\\&\le2M\mathbb{I}_{\{|X|>R\}}+2M\mathbb{I}_{\{|X_n-X|>\delta\}}+\frac{\epsilon}{3}\end{align*}
が成り立つ.よって,$n>N$なら
\begin{align*}&|\mathbb{E}[f(X_n)]-\mathbb{E}[f(X)]|
\\&\le2M\mathbb{E}\brc{\mathbb{I}_{\{|X|>R\}}}+2M\mathbb{E}\brc{\mathbb{I}_{\{|X_n-X|>\delta\}}}+\frac{\epsilon}{3}
\\&<2M\cdot\frac{\epsilon}{6M}+2M\cdot\frac{\epsilon}{6M}+\frac{\epsilon}{3}=\epsilon\end{align*}
が従う.すなわち,$\{X_n\}_{n\in\N}$は$X$に分布収束する.
実は「確率収束する確率変数列$\{X_n\}_n$は概収束する確率変数列$\{X_{n(k)}\}_k$をもつ」という事実を用いればより簡単に証明できます.
しかし,この事実を証明するためにはボレル-カンテリの補題を用いるので,ここでは前提知識の少ない証明を与えました.
4つの収束をする例としない例
いま4つの確率変数の収束の強弱を証明しましたが,たとえば「分布収束するが確率収束しないような確率変数列があるか」といった,弱い収束はするが強い収束はしないような例については考えてきませんでした.
そこで,最後にそのような関数列の例を考えましょう.
強さの異なる似た概念があるとき,一方は満たすが他方は満たさないような例を知っておくことが良い理解に繋がることはよくあります.
確率収束も概収束もするが$p$次平均収束しない例
閉区間$[0,1]$上の一様分布の確率測度$\mathbb{P}$を考える.この確率空間$([0,1],\mathcal{B}([0,1]),\mathbb{P})$上の確率変数
\begin{align*}X_{n}(\omega)=\begin{cases}n,&0\le \omega\le\frac{1}{n},\\0,&\frac{1}{n}<\omega\le1,\end{cases}\quad
X(\omega)\equiv0\end{align*}
を定める($n=0,1,\dots,k-1$).このとき,確率変数列$\{X_n\}$が$X$に確率収束も概収束もするが,$p$次平均収束($p\ge1$)しないことを示せ.
上で示した収束の強弱から概収束している時点で確率収束するのは当たり前ですが,ここでは確率収束しないことも定義に基づいて示しておきます.
確率収束することの証明
任意に$\epsilon\in(0,1)$をとる.
\begin{align*}\mathbb{P}\bra{|X-X_n|>\epsilon}=\mathbb{P}\bra{\brc{0,\frac{1}{n}}}=\frac{1}{n}\xrightarrow[]{n\to\infty}0\end{align*}
が成り立つ.よって,確率変数列$\{X_n\}$は$X$に確率収束する.
概収束することの証明
任意に$\omega\in(0,1]$をとる.任意の$\epsilon>0$をとる.
ある$N\in\N$が存在して$\frac{1}{N}<\omega$となるから,$n>N$で
\begin{align*}|X(\omega)-X_n(\omega)|=0<\epsilon\end{align*}
となり,ε-N論法により$\lim\limits_{n\to\infty}X_n(\omega)=X(\omega)$を得る.一方,$\{X_n(0)\}$は$X(0)$に収束しない.よって,
\begin{align*}\mathbb{P}\bra{\set{\omega\in[0,1]}{\lim_{n\to\infty}X_n(\omega)=X(\omega)}}=\mathbb{P}((0,1])=1\end{align*}
なので,確率変数列$\{X_n\}$は$X$に概収束する.
$p$次平均収束しないことの証明
$|X-X_n|^p$がとる値は0または$n^p$である.よって,期待値の定義より
\begin{align*}&E[|X-X_n|^p]=0\times \mathbb{P}(X-X_n=0)+n^p\times \mathbb{P}(X-X_n=n)
\\&=n^p\times\frac{1}{n}=n^{p-1}\xrightarrow[]{n\to\infty}\begin{cases}\infty,&p>1,\\1,&p=1\end{cases}\end{align*}
なので,確率変数列$\{X_n\}$は$X$に$p$次平均収束しない.
$X_n$と$X$が異なるのは$[0,\frac{1}{n}]$部分ですが,$n$を大きくするほど$X_n(\omega)\neq0$となる0付近の$\omega$がどんどん狭くなり,$(0,1]$上で$\{X_n\}$が0に各点収束することになります.
一方,$p$次平均収束は期待値を考えるので「$X_n$と$X$がどれくらい離れているか」ということも影響します.$n$を大きくすると$[0,\frac{1}{n}]$での離れ具合も大きくなり,$p$次平均収束しないわけですね.
確率収束も$p$次平均収束もするが概収束しない例
閉区間$[0,1]$上の一様分布の確率測度$\mathbb{P}$を考える.この確率空間$([0,1],\mathcal{B}([0,1]),\mathbb{P})$上の確率変数
\begin{align*}X_{\frac{k(k-1)}{2}+\ell}(\omega)=\begin{cases}1,&\frac{\ell}{k}\le \omega\le\frac{\ell+1}{k},\\0,&\text{other},\end{cases}\quad
X(\omega)\equiv0\end{align*}
を定める($k=1,2,3,\dots$, $\ell=0,1,\dots,k-1$).このとき,確率変数列$\{X_n\}$が$X$に確率収束も$p$次平均収束($p\ge1$)もするが,概収束しないことを示せ.
上で示した収束の強弱から$p$次平均収束している時点で確率収束するのは当たり前ですが,ここでは確率収束しないことも定義に基づいて示しておきます.
確率変数$X_n$について,$n=\frac{k(k-1)}{2}+\ell$と表す($k=1,2,3,\dots$, $\ell=0,1,\dots,k-1$).
確率収束することの証明
任意に$\epsilon\in(0,1)$をとる.$n\to\infty\iff k\to\infty$だから,
\begin{align*}\mathbb{P}\bra{|X-X_n|>\epsilon}=\mathbb{P}\bra{\abs{X-X_{\frac{k(k-1)}{2}+\ell}}>\epsilon}=\mathbb{P}\bra{\brc{\frac{\ell}{k},\frac{\ell+1}{k}}}=\frac{1}{k}\xrightarrow[]{n\to\infty}0\end{align*}
が成り立つ.よって,確率変数列$\{X_n\}$は$X$に確率収束する.
$p$次平均収束することの証明
$|X_n-X|^p$がとる値は0または1である.よって,期待値の定義より
\begin{align*}E[|X_n-X|^p]&=0\times \mathbb{P}(X_n-X=0)+1\times \mathbb{P}(X_n-X=1)
\\&=\mathbb{P}\bra{X_{\frac{k(k-1)}{2}+\ell}-X=1}=\frac{1}{k}\xrightarrow[]{n\to\infty}0\end{align*}
が成り立つ.よって,確率変数列$\{X_n\}$は$X$に$p$次平均収束する.
概収束しないことの証明
任意の$\omega\in[0,1]$を考える.
任意の$N\in\N$に対して,$n=\frac{k(k-1)}{2}+\ell>N$を満たすある$k\in\{1,2,3,\dots\}$, $\ell\in\{0,1,\dots,k-1\}$が存在して,$\frac{\ell}{k}\le\omega\le\frac{\ell+1}{k}$となり,このとき
\begin{align*}X(\omega)-X_n(\omega)=1-0=1\end{align*}
となるから,確率変数列$\{X_n\}$は$X$に概収束しない.
$X_n$と$X$が異なるのは$[\frac{\ell}{k},\frac{\ell+1}{k}]$部分ですが,$n$を大きくすれば$k$も大きくなり,この部分は狭くなっていき$X\equiv0$に確率収束も$p$次平均収束もします.
一方,どの$\omega\in[0,1]$に対しても$X_n(\omega)=1$となる$n$が無限に存在するため実数列$\{X_n(\omega)\}$は収束せず,確率変数列$\{X_n\}$は概収束しないわけですね.
分布収束するが確率収束しない例
分布収束は異なる関数空間上で定義された$X_n$と$X$に対しても定義されるので,そのような$X_n$と$X$を考えれば$X$に分布収束するが確率収束しないような確率変数列$\{X_n\}$は簡単に作れます.
しかし,それでは分布収束と確率収束の違いの理解につながらないので,同じ確率空間上の$X_n$と$X$で分布収束するが確率収束しないような例を考えましょう.
閉区間$[0,1]$上の一様分布の確率測度$\mathbb{P}$を考える.この確率空間$([0,1],\mathcal{B}([0,1]),\mathbb{P})$上の確率変数
\begin{align*}X_n(\omega)=\begin{cases}1,&0\le \omega<\frac{1}{2},\\0,&\frac{1}{2}\le \omega\le1,\end{cases}\quad
X(\omega)=\begin{cases}0,&0\le \omega<\frac{1}{2},\\1,&\frac{1}{2}\le \omega\le1,\end{cases}\end{align*}
を定める($n=1,2,\dots$).このとき,確率変数列$\{X_n\}$が$X$に分布収束するが,確率収束しないことを示せ.
分布収束することの証明
任意の実数値有界連続関数$f$をとる.$X_n$と$X$がとる値は0,1だから,$f(X_n)$と$f(X)$がとる値は$f(0)$, $f(1)$である.
よって,期待値の定義より,$n$によらず
\begin{align*}&E[f(X_n)]=f(0)\times \mathbb{P}(X_n=0)+f(1)\times \mathbb{P}(X_n=1)=\frac{1}{2}f(0)+\frac{1}{2}f(1),
\\&E[f(X)]=f(0)\times \mathbb{P}(X=0)+f(1)\times \mathbb{P}(X=1)=\frac{1}{2}f(0)+\frac{1}{2}f(1)\end{align*}
だから$E[f(X_n)]=E[f(X)]$となる.これは$\lim\limits_{n\to\infty}E[f(X_n)]=E[f(X)]$でもあるから,確率変数列$\{X_n\}$は$X$に分布収束する.
確率収束しないことの証明
$n$によらず
\begin{align*}P\bra{|X-X_n|>\frac{1}{2}}=1\end{align*}
だから,確率変数列$\{X_n\}$は$X$に確率収束しない.
$X_n$, $X$自体が大きく異なっていても,全体の確率分布が近くなっていれば分布収束します.いまの問題では$X_n$も$X$もそもそも同じベルヌーイ分布$\mrm{Ber}(\frac{1}{2})$に従っており分布収束します.
一方,確率収束は確率変数自体が近付いていくことが要求されているので,いまの問題では$X_n$と$X$がとる値自体は大きく異なっており確率収束しないわけですね.

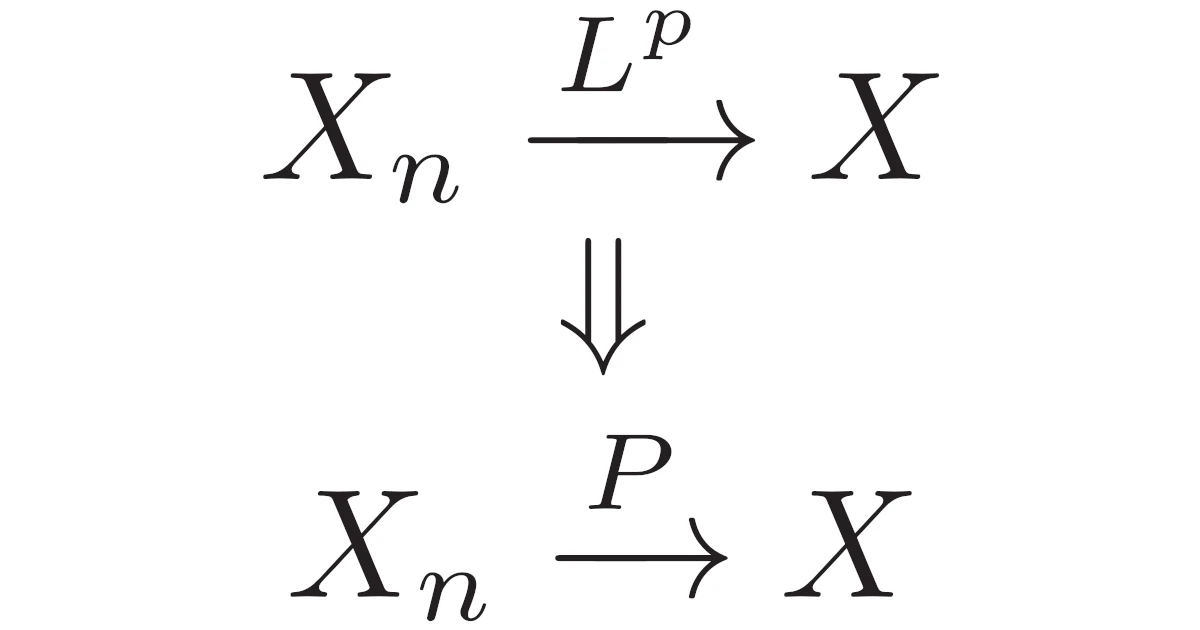

コメント