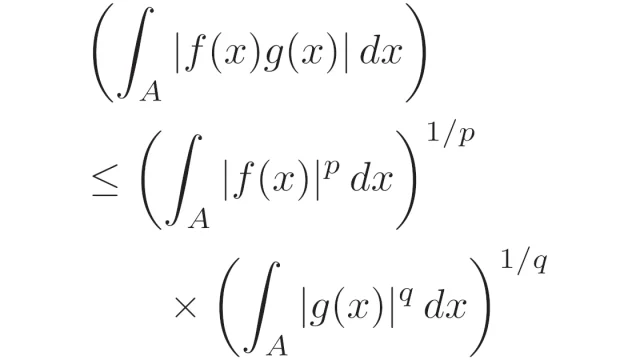 ルベーグ空間
ルベーグ空間 ヘルダーの不等式の証明・応用|ルベーグ積分の基本不等式
ルベーグ積分(測度論)を扱う分野では「ヘルダーの不等式」は基本的な不等式のひとつとして重要です.この記事では,ヘルダーの不等式の証明と,ヘルダーの不等式の応用(双対性)を説明します.
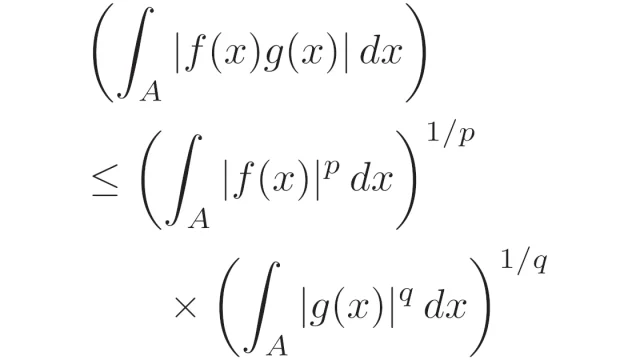 ルベーグ空間
ルベーグ空間  ルベーグ空間
ルベーグ空間  ルベーグ空間
ルベーグ空間  群論の基本
群論の基本  線形空間の基本
線形空間の基本 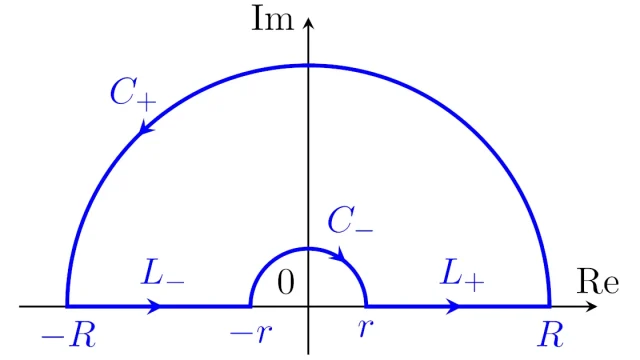 複素解析
複素解析 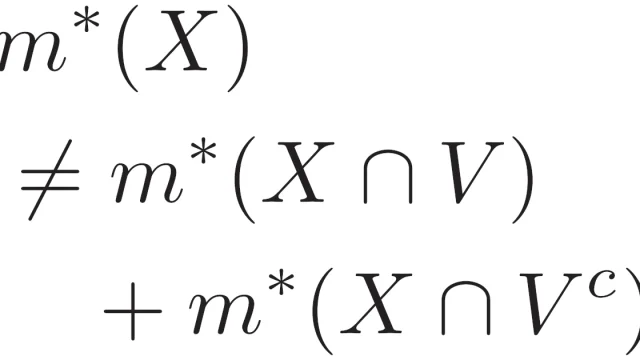 ルベーグ積分
ルベーグ積分 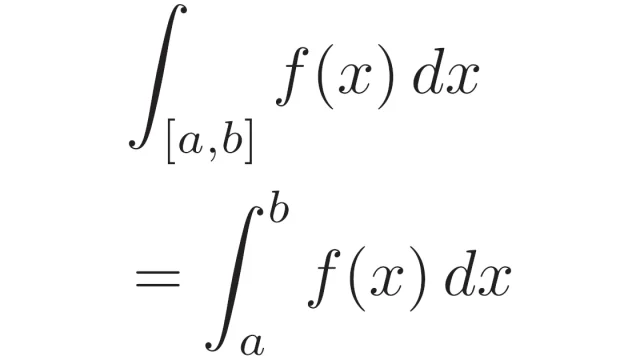 ルベーグ積分の基本
ルベーグ積分の基本 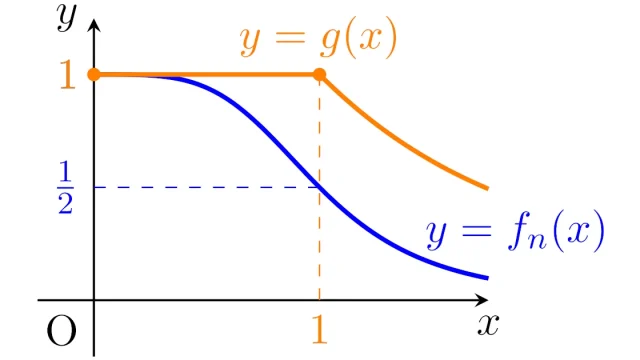 ルベーグ積分の基本
ルベーグ積分の基本 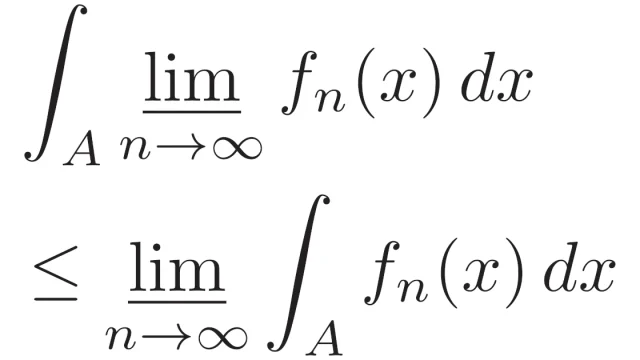 ルベーグ積分の基本
ルベーグ積分の基本