数列の収束の定義（ε-N論法）｜例題から考え方を理解しよう

目次

1. 微分積分学の参考文献
   1. 微分積分学（笠原晧司 著）
2. $\epsilon\text{-}N$論法のための準備
   1. 絶対値は数直線上の距離を表す
   2. 実数列は横軸$n$，縦軸$a_n$の平面に図示できる
3. 数列の収束の定義（$\epsilon\text{-}N$論法）
   1. 実数列$\{a_n\}$の項$a_n$と極限との誤差に注目する
   2. $\epsilon\text{-}N$論法による実数列の収束の定義
4. $\epsilon\text{-}N$論法の具体例
   1. 具体例１（$a_n=1/n$）
   2. 具体例２（$a_n=(n-2)/n$）
   3. 具体例３（$a_n=1/n^2$）

微分積分学の参考文献

以下は微分積分学に関するオススメの教科書です．

微分積分学（笠原晧司 著）

数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．

$\epsilon\text{-}N$論法のための準備

$\epsilon\text{-}N$論法のために，絶対値の図形的な意味と実数列の図示を整理しておきましょう．

絶対値は数直線上の距離を表す

高校数学で実数の絶対値は次のように定義したのでした．

実数$a$に対して，$a$と原点$0$との距離を$a$の絶対値（absolute value）といい，$|a|$と表す．

この定義から次は簡単に得られますね．

実数$a$, $b$に対して，$|a-b|$は$a$と$b$の距離を表す．

数直線上の$0$, $a-b$を$+b$平行移動すると，それぞれ$b$, $a$に移るから

$(\text{$0$と$a-b$の距離})=(\text{$b$と$a$の距離})$

である．絶対値の定義から$(\text{$0$と$a-b$の距離})=|a-b|$であることと併せて，

$(\text{$0$, $a-b$の距離})=|a-b|$

を得る．

このことから，$|a-b|<c$は「$a$と$b$の誤差が$c$未満」という意味の不等式であると言えますね．

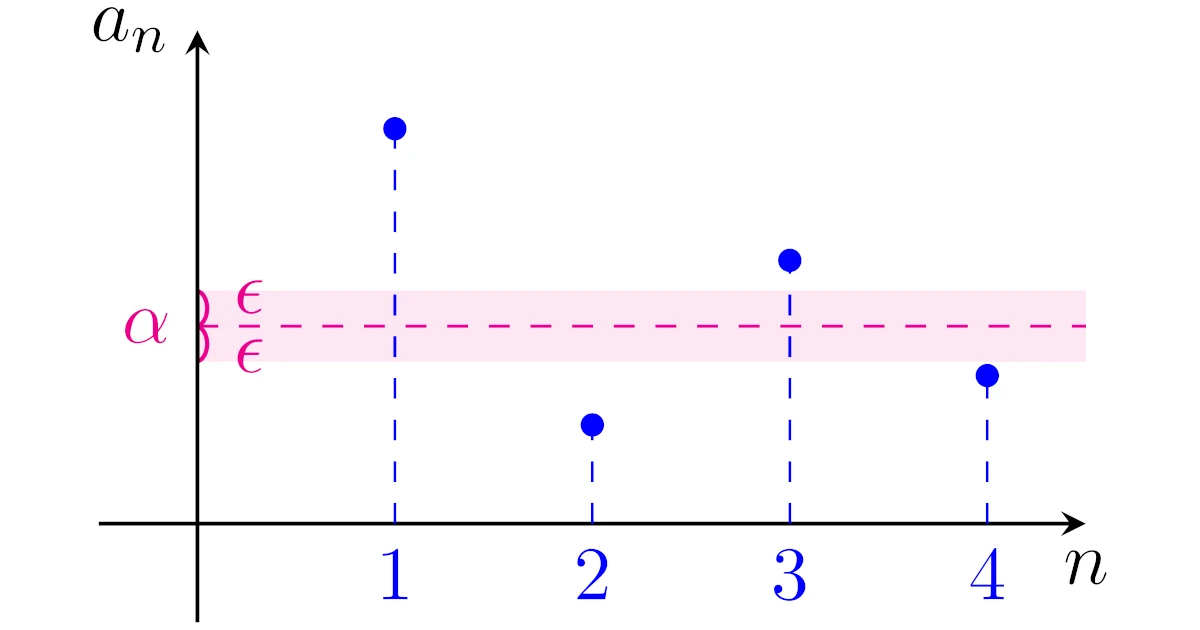
実数列は横軸$n$，縦軸$a_n$の平面に図示できる

実数列$\{a_n\}$は$n$を１つ決めれば，１つ実数が決まります．

このことから，実数列$\{a_n\}$は横軸$n$，縦軸$a_n$として図示することができます．

例えば，一般項$a_n=1+\dfrac{(-1)^{n-1}}{n}$の実数列$\{a_n\}$は下図のように図示できますね．

図を描けば数列$\{a_n\}$の値が$n$を大きくするにつれて１に近付いていることは視覚的にも見てとれますね．

数列の収束の定義（$\epsilon\text{-}N$論法）

まず$\epsilon\text{-}N$論法の考え方を説明してから，きちんとした定義を述べます．

実数列$\{a_n\}$の項$a_n$と極限との誤差に注目する

例えば，一般項$a_n=1+\dfrac{(-1)^{n-1}}{n}$の実数列$\{a_n\}$を考えましょう．

$a_n$はどんどん１に近付いていくので，これは「$n$を十分大きくすれば$a_n$と１の誤差$|a_n-1|$がどこまでも０に近くなる」ということができますね．

これは「どんなに小さな正の数$\epsilon$に対しても，十分大きい$n$に対して$a_n$と１の誤差$|a_n-1|$は$\epsilon$未満になる」と言い換えられます．

具体的に$\epsilon=0.3$として，いつ$a_n$と１の誤差$|a_n-1|$は$\epsilon$未満になるかを考えてみましょう．いま

\begin{align*}|a_n-1|=\abs{\bra{1+\frac{(-1)^{n-1}}{n}}-1}=\frac{1}{n}\end{align*}

ですから，この誤差$|a_n-1|$が$\epsilon=0.3$未満となるのは$n=4,5,6,\dots$のときですね．

つまり，$n>3$のとき$|a_n-1|<0.3$となり，下図のように図示できますね．

同じ要領で考えれば，$\epsilon=0.1$なら$n>10$のとき$|a_n-1|<\epsilon$となりますし，もっと小さい$\epsilon=0.001$でも$n>1000$のとき$|a_n-1|<\epsilon$となりますね．

ここで大切なことは，どんなに小さな正の数$\epsilon$に対しても，十分大きな正の整数$N$があって，$n>N$のとき$|a_n-1|<\epsilon$となってくれるという点です．

$\epsilon\text{-}N$論法による実数列の収束の定義

以上の考え方をふまえて$\epsilon\text{-}N$論法により実数列の収束を定義しましょう．

実数列$\{a_n\}$が$\alpha\in\R$に収束するとは，任意の$\epsilon>0$に対して，ある$N\in\N$が存在して，

\begin{align*}n>N\Ra|a_n-\alpha|<\epsilon\end{align*}

が成り立つことをいう．また，このとき$\lim\limits_{n\to\infty}a_n=\alpha$や$a_n\to\alpha\ (n\to\infty)$などと表す．

少し砕けた言い方をすれば，「どんなに小さな正の数$\epsilon$に対しても，十分大きな正の整数$N$をうまくとって，$n>N\Ra|a_n-\alpha|<\epsilon$が成り立つようにできる」というときに，$\{a_n\}$が$\alpha$に収束するというわけですね．

$\epsilon$と$N$を用いて表現することが多いことから，この数列の収束の定義の論法を$\epsilon\text{-}N$論法といいます．

また，上の考え方からも分かるように，$N$は$\epsilon$に応じて決めてよいという点は大切です．

$\epsilon\text{-}N$論法の具体例

いくつか具体例を考えましょう．

具体例１（$a_n=1/n$）

この問題では$n>N$のとき

\begin{align*}|a_n-0|=\frac{1}{n}<\frac{1}{N}\end{align*}

となります．よって，$\epsilon>0$に対して$n>N$のときに$|a_n-0|<\epsilon$が成り立つには，

\begin{align*}\dfrac{1}{N}<\epsilon\iff N>\frac{1}{\epsilon}\end{align*}

が成り立つように正の整数$N$をとれば良いですね．

例えば，$\frac{1}{\epsilon}$以上の最小の整数$\lceil\frac{1}{\epsilon}\rceil$を$N$とすれば良いですね．

このように$\epsilon\text{-}N$論法を用いた数列の収束の証明では，どのように$N$をとれば$n>N\Ra|a_n-\alpha|<\epsilon$が成り立つかを考えることがポイントとなります．

答案の中では$N$が先に定めて$n>N\Ra|a_n-0|<\epsilon$を示していますが，思考プロセスは

• $|a_n-0|=\frac{1}{n}<\frac{1}{N}$
• $N>\frac{1}{\epsilon}$となる$N\in\N$をとればよい
• $N:=\lceil\frac{1}{\epsilon}\rceil$とすればよい

の順番になっていることに注意してください．

具体例２（$a_n=(n-2)/n$）

この問題では$n>N$のとき

\begin{align*}|a_n-1|=\abs{-\frac{2}{n}}=\frac{2}{n}<\frac{2}{N}\end{align*}

となります．よって，$\epsilon>0$に対して$n>N$のときに$|a_n-1|<\epsilon$が成り立つには，

\begin{align*}\dfrac{2}{N}<\epsilon\iff N>\frac{2}{\epsilon}\end{align*}

が成り立つように正の整数$N$をとれば良いので，例えば$N=\lceil\frac{2}{\epsilon}\rceil$とすれば良いですね．

具体例３（$a_n=1/n^2$）

この問題では$n>N$のとき

\begin{align*}|a_n-0|=\frac{1}{n^2}<\frac{1}{N^2}\end{align*}

となります．よって，$\epsilon>0$に対して$n>N$のときに$|a_n-0|<\epsilon$が成り立つには，

\begin{align*}\dfrac{1}{N^2}<\epsilon\iff N>\frac{1}{\sqrt{\epsilon}}\end{align*}

が成り立つように正の整数$N$をとれば良いので，例えば$N=\lceil\frac{1}{\sqrt{\epsilon}}\rceil$とすれば良いですね．