コーシーの関数方程式｜f(x+y)=f(x)+f(y)を満たす連続関数f

微分積分学
2022.07.19
微分積分学

$f(x)=ax$の形の関数$f:\R\to\R$は

    \begin{align*}f(x+y)=a(x+y)=ax+ay=f(x)+f(y)\end{align*}

となって$f(x+y)=f(x)+f(y)$を満たします．そこで，この記事では次の問題を考えましょう．

任意の$x,y\in\R$に対して等式

    \begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\R)\end{align*}

をみたす連続関数$f:\R\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限るか？

この問題は「$f$が連続関数のとき，$f(x)=ax$の形をしていないが等式を満たすものが存在するかどうか」を聞いているわけですね．

このように等式を満たす未知関数を求める問題を関数方程式といい，この問題の関数方程式$f(x+y)=f(x)+f(y)$をコーシー（Cauchy）の関数方程式といいます．

結論から言えば，問題の連続関数$f$は$f(x)=ax$の形に限ることが証明できます．

問題を解く２つのポイント

この問題のポイントは

  • 有理数全部の集合$\Q$の稠密性
  • 関数の連続性

の２つです．

有理数の集合$\Q$の稠密性

数直線上に有理数は極めて密に存在しており，次が成り立ちます．

任意の$x\in\R$に対して，$x$に収束する有理数列$\{r_n\}$が存在する．

任意の$n\in\N$に対して

    \begin{align*}\bra{x+\frac{1}{2n}}-\bra{x-\frac{1}{2n}}=\frac{1}{n}\end{align*}

なので，

    \begin{align*}x-\frac{1}{2n}\le \frac{k_n}{n}<x+\frac{1}{2n}\end{align*}

を満たす有理数$r_n:=\dfrac{k_n}{n}$がただひとつ存在する．

このとき，はさみうちの原理より有理数列$\{r_n\}$は$x$に収束する．

この証明では具体的に$r_n$をとっているので選択公理は必要ありませんね．

「どの実数のどんなに近くにも有理数が存在している」「数直線をどこまで「拡大」しても有理数が存在している」と言い換えることもできますね．

この性質を$\R$における$\Q$の稠密性といい，次のように表すことも多いので覚えておくと良いでしょう．

任意の$x\in\R$と$\epsilon>0$に対して，

    \begin{align*}x-\epsilon<r<x+\epsilon\end{align*}

を満たす$r\in\Q$が存在する．

関数の連続性

連続関数の定義から直ちに次が得られます．

関数$f:\R\to\R$を考える．$f$が連続なら，任意の$x\in\R$と，$x$に収束する実数列$\{x_{n}\}$に対して

    \begin{align*}\lim_{n\to\infty}f(x_{n})=f(x)\end{align*}

が成り立つ．

$x=\lim\limits_{n\to\infty}x_n$ですから，この等式は

    \begin{align*}\lim_{n\to\infty}f(x_{n})=f\bra{\lim_{n\to\infty}x_n}\end{align*}

とも表せます．つまり，連続関数は「極限と交換できる関数」ということができますね．

問題の解答

まずは連続でないときにも成り立つ補題を示し，その補題を用いて問題を解きましょう．

補題

任意の$x,y\in\R$に対して，コーシーの関数方程式

    \begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\Q)\end{align*}

をみたす関数$f:\Q\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限る．

冒頭の問題との違いは，関数$f$の定義域が$\Q$となっている点です．

この場合，実は$f$に連続性を課さなくても$f(x)=ax$の形のものに限ることが証明できるわけですね．

［ステップ１］任意の$p\in\Z$に対して，$f(p)=pf(1)$が成り立つことを示す．

(i) $p\ge0$のときに成り立つことを数学的帰納法により示す．

$f(0)=f(0+0)=f(0)+f(0)$から$f(0)=0=0f(1)$が成り立つ．また，ある$p\ge0$で成り立ったと仮定すると，コーシーの関数方程式を用いて

    \begin{align*}f(p+1)=&f(p)+f(1)\\=&pf(1)+f(1)=(p+1)f(x)\end{align*}

が従う．よって，任意の$p\ge0$に対して$f(p)=pf(1)$が成り立つ．

(ii) $p<0$のときは，$-p>0$より(i)を利用して$f(-p)=-pf(1)$が成り立つから

    \begin{align*}0=&f(0)=f(p+(-p)) \\=&f(p)+f(-p)=f(p)-pf(1)\end{align*}

となり，移項して$f(p)=pf(1)$が従う．

［ステップ２］任意の$q\in\N$に対して，$f\bigl(\frac{p}{q}\bigr)=\frac{1}{q}f(p)$が成り立つことを示す．

$p$を$p=\frac{p}{q}+\frac{p}{q}+\dots+\frac{p}{q}$と$q$項に分ければ，コーシーの関数方程式を繰り返し用いて

    \begin{align*}f(p)=f\bra{\frac{p}{q}}+f\bra{\frac{p}{q}}+\dots+f\bra{\frac{p}{q}}=qf\bra{\frac{p}{q}}\end{align*}

が成り立つ（厳密には数学的帰納法）．

よって，$f(p)=qf\bigl(\frac{p}{q}\bigr)$の両辺を$q$で割って$f\bigl(\frac{p}{q}\bigr)=\frac{1}{q}f(p)$を得る．

［ステップ３］$f$は$f(x)=ax$ ($a\in\R$)の形のものに限ることを示す．

任意の有理数$x$をとる．$x=\frac{p}{q}$ ($p\in\Z$, $q\in\N$)と表すと，以上の[１]と[２]を併せて

    \begin{align*}f(x)=f\bra{\frac{p}{q}}=\frac{1}{q}f(p)=\frac{p}{q}f(1)=f(1)x\end{align*}

が成り立つ．よって，$a:=f(1)\in\R$とすれば，$f(x)=ax$と表せることが分かる．

この補題の証明では全ての有理数が$1$を$p$倍 ($p\in\Z$)，$\dfrac{1}{q}$倍 ($q\in\Z\setminus\{0\}$)することで表せることがポイントとなっています．

このため，$x=1$を基準にした帰納法により$f(x)=f(1)x$ ($x\in\Q$)となることを示すことができるわけですね．

解答

それでは，いま示した補題を用いて冒頭の問題を解きましょう．

（再掲）任意の$x,y\in\R$に対して等式

    \begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\R)\end{align*}

をみたす連続関数$f:\R\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限るか？

補題より，ある$a\in\R$が存在して，任意の有理数$x\in\Q$に対して，$f(x)=ax$が成り立つ．

また，$\R$における$\Q$の稠密性から，任意の$x\in\R$に対して，$x_n\to x$となる$\Q$の列$\{x_n\}_{n\in\N}$が存在する．

$f$の連続性より

    \begin{align*}f(x)=&f\bra{\lim\limits_{n\to\infty}x_n}=\lim\limits_{n\to\infty}f(x_n) \\=&\lim\limits_{n\to\infty}ax_n=ax\end{align*}

となる．よって，任意の$x\in\R$に対して，$f(x)=ax$が成り立つ．

関数$f$の連続性と有理数の集合$\Q$の稠密性が見事に噛み合っていますね．

補足

２つ補足します．

１点で連続な場合

いまの問題で$f$は$\R$上で連続なものを考えましたが，実はただ１点でさえ連続なら$f(x)=ax$の形に限ることが証明できます．

すなわち，問題より条件を緩めた次が成り立ちます．

$c\in\R$とする．任意の$x,y\in\R$に対して等式

    \begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\R)\end{align*}

をみたす点$c$で連続な関数$f:\R\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限る．

$f$は点$c$で連続だから，

    \begin{align*}\lim_{h\to0}(f(c+h)-f(c))=0\end{align*}

が成り立つ．このことから，任意の$x\in\R$に対して

    \begin{align*}&\lim_{h\to0}(f(x+h)-f(x)) \\=&\lim_{h\to0}\{f((x-c)+(c+h))-f((x-c)+c))\} \\=&\lim_{h\to0}\{(f(x-c)+f(c+h))-(f(x-c)+f(c))\} \\=&\lim_{h\to0}(f(c+h)-f(c))=0\end{align*}

となって，$f$は$\R$上で連続である．

よって，上の問題で示したように$f$は$f(x)=ax$ ($a\in\R$)の形のものに限る．

点$c$に条件はありませんから，$f$がどの点で連続であったとしても，コーシーの関数方程式と併せると自動的に$\R$全体で連続になるわけですね．

類似の関数方程式

コーシーの関数方程式の類次の関数方程式として次のものを考えることもあります．

  • $f(x+y)=f(x)f(y)$
  • $g(xy)=g(x)+g(y)$
  • $h(xy)=h(x)h(y)$

ただし，$f:\R\to\R$, $g,h:\R_{+}\to\R$で，$\R_{+}$は正の実数全部の集合です．

コーシーの関数方程式と同様に有理数で考えてから$\R$における$\Q$の稠密性を用いれば，連続関数解はそれぞれ

  • $f(x)=a^x$
  • $g(x)=a\log{x}$
  • $h(x)=x^a$

となることが証明できます．

例えば，１つ目の$f(x+y)=f(x)f(y)$はポアソン過程を学ぶ際に登場することもありますね．

ハメル基底と反例

冒頭でも軽く触れましたが，$f$の連続性を外した次の問題は「限らない」となります．

（再掲）任意の$x,y\in\R$に対して等式

    \begin{align*}f(x+y)=f(x)+f(y)\quad(x,y\in\R)\end{align*}

をみたす関数$f:\R\to\R$は$f(x)=ax$ ($a\in\R$)の形のものに限るか？

つまり，コーシーの関数方程式を満たすが$f(x)=ax$の形をしていない関数$f$が，ハメル基底というものを用いることで構成することができます．

詳しくは以下の記事を参照してください．

ハメル基底とコーシーの関数方程式｜$f(x+y)=f(x)+f(y)$
等式f(x+y)=f(x)+f(y)を満たす関数にはどんなものがあるでしょうか？たとえば単純な比例の関数f(x)=axはこの等式を満たしますが，他にはないのでしょうか？実は「ハメル基底」を用いることで，この等式を満たす比例でない関数が構成できます．
math-note.xyz

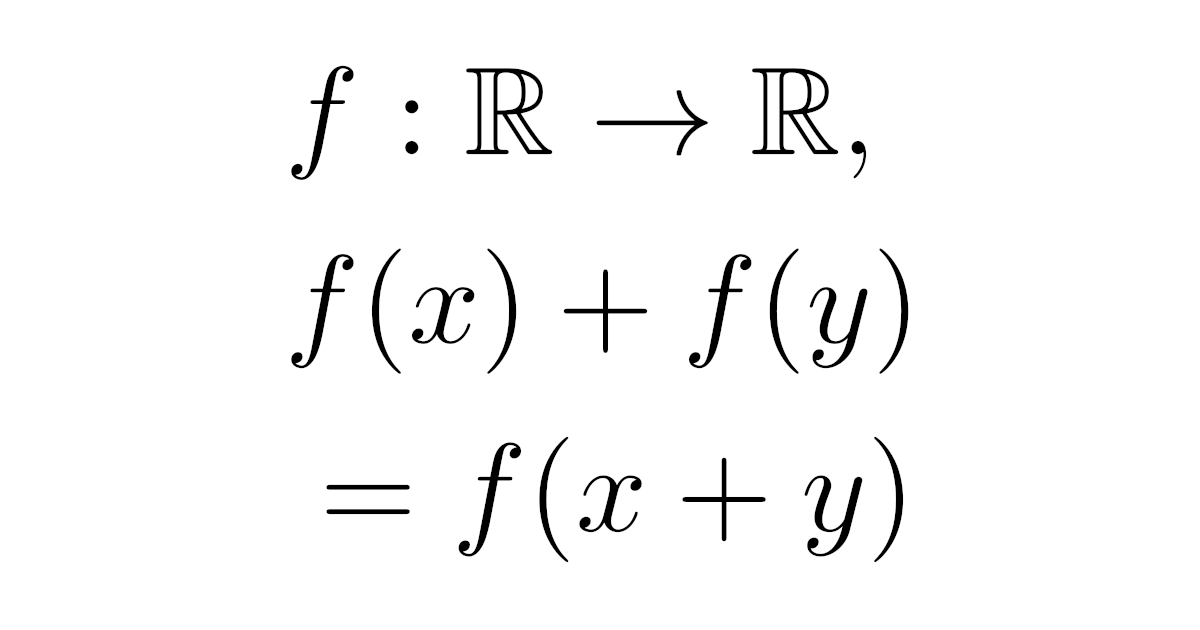
コメント