ガウス関数のフーリエ変換｜微分方程式を用いて計算する

次の形の式で定まる関数$G:\R\to\R$を（１次元の）ガウス（Gauss）関数といい，数学のさまざまな分野で現れます．

$\begin{align*}G(x)=A\exp{\bra{-\frac{(x-\mu)^2}{2\sigma^2}}}\quad(\mu\in\R,\sigma>0)\end{align*}$

例えば，確率・統計の分野において，平均$\mu$，分散$\sigma^2$の正規分布の確率密度関数がガウス関数$G$であることはよく知られていますね．

さて，以前の記事で$\mu=0$のガウス関数$G$にフーリエ（Fourier）変換$\mathcal{F}$を施してできる関数$\mathcal{F}[G]=\hat{G}$もガウス関数であることをコーシーの積分定理を用いて示しました．

ガウス関数のフーリエ変換１｜コーシーの積分定理から計算する

ガウス関数にはフーリエ変換を施してもガウス関数に戻るという性質があります．この記事では，ガウス関数の定義とフーリエ変換の定義を確認したのち，ガウス関数のフーリエ変換をコーシーの積分定理を用いて計算します．

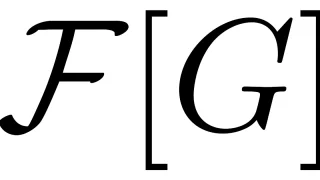
実はこのことは微分方程式を解くことでも示すこともできます．

この記事では

１階線形常微分方程式
ガウス関数のフーリエ変換

を順に説明します．

なお，この記事のフーリエ変換は

$\begin{align*}\mathcal{F}[f]=\hat{f}=\frac{1}{\sqrt{2\pi}}\int_{\R}f(x)e^{-ix\xi}\,dx\end{align*}$

で定めるものとします．

１階線形常微分方程式
ガウス関数のフーリエ変換

１階線形常微分方程式

未知関数$u$，変数$t$の常微分方程式で

$\begin{align*}\od{u}{t}(t)+P(t)u(t)=Q(t)\end{align*}$

の形をしてた微分方程式を１階線形常微分方程式といいます．

１階線形常微分方程式

$\begin{align*}\od{u}{t}(t)+P(t)u(t)=Q(t)\quad\dots(*)\end{align*}$

を考える．関数$I$を関数$P$の不定積分の１つとするとき，微分方程式の両辺に$e^{I(t)}$をかけることで

$\begin{align*}u(t)=e^{-I(t)}\int e^{I(t)}Q(t)\,dt\end{align*}$

と解ける．

これは公式というより，考え方から理解して使えるようになりたい命題です．

微分方程式の両辺に$e^{I(t)}$をかけることで

$\begin{align*}&e^{I(t)}\od{u}{t}(t)+e^{I(t)}P(t)u(t)=e^{I(t)}Q(t) \\\iff&\od{}{t}\bra{e^{I(t)}u(t)}=e^{I(t)}Q(t) \iff e^{I(t)}u(t)=\int e^{I(t)}Q(t)\,dt \\\iff&u(t)=e^{-I(t)}\int e^{I(t)}Q(t)\,dt\end{align*}$

と解ける．

左辺が

$\begin{align*}e^{I(t)}\od{u}{t}(t)+e^{I(t)}P(t)u(t)=\od{}{t}\bra{e^{I(t)}u(t)}\end{align*}$

と微分を１つにまとめられるので，うまく計算できているわけですね．

積分因子$e^{I(t)}$をかけて左辺を完全微分形にして解いたということもできますね．

ガウス関数のフーリエ変換

$\mu=0$のガウス関数$G$のフーリエ変換$\hat{G}$が１階線形常微分方程式を満たすことから$\hat{G}$を求めましょう．

なお，ガウス関数のフーリエ変換が定義できることは冒頭でも紹介した記事を参照してください．

ガウス関数のフーリエ変換１｜コーシーの積分定理から計算する

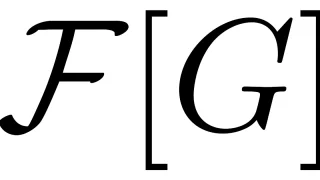
$\mu\in\R$, $\sigma>0$に対して，

$\begin{align*}G(x)=A\exp{\bra{-\frac{x^2}{2\sigma^2}}}\end{align*}$

で定まるガウス関数$G$のフーリエ変換$\hat{G}$は

$\begin{align*}\hat{G}=A\sigma\exp{\bra{-\frac{1}{2}\sigma^2\xi^2}}\end{align*}$

となる．よって，$\hat{G}$もガウス関数である．

$\hat{G}$が微分方程式の初期値問題

$\begin{align*}\begin{cases}\displaystyle\od{\hat{G}}{\xi}(\xi)+\sigma^2\xi\hat{G}(\xi)=0\\\hat{G}(0)=\dfrac{A}{\sqrt{2\mu}}\end{cases}\end{align*}$

の解であることを示し，この微分方程式を解くことで$\hat{G}$を求めます．

$\mu=\dfrac{1}{2\sigma^2}$とおく．すなわち，$G(x)=Ae^{-\mu x^2}$とする．

ステップ１（$\hat{G}(0)$の値）

まず$\hat{G}(0)$は

$\begin{align*}\hat{G}(0) =&\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}G(x)e^{-i0x}\,dx \\=&\frac{A}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\mu x^2}\,dx \\=&\frac{A}{\sqrt{2\pi}}\cdot\sqrt{\frac{\pi}{\mu}} =\frac{A}{\sqrt{2\mu}} =A\sigma\end{align*}$

である．ただし，一番下の行の最初の等式ではガウス積分

$\begin{align*}\int_{-\infty}^{\infty}e^{-x^2}\,dx=\sqrt{\pi}\end{align*}$

を用いた（正確にはガウス積分に変数変換$x\mapsto\sqrt{\mu}x$を施した積分）．

ステップ２（$\hat{G}$が満たす微分方程式）

次に対称性を用いて

$\begin{align*}\int_{-\infty}^{\infty}|xG(x)|\,dx =&2A\int_{0}^{\infty}xe^{-\mu x^2}\,dx \\=&2A\brc{-\frac{1}{2\mu}e^{-\mu x^2}}_{0}^{\infty} =\frac{A}{\mu}<\infty\end{align*}$

だから，$\hat{G}$は微分可能で

$\begin{align*}\od{\hat{G}}{\xi}(\xi) =&\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}(-ix)G(x)e^{-i\xi x}\,dx \\=&\frac{A}{\sqrt{2\pi}}\int_{-\infty}^{\infty}(-ix)e^{-\mu x^2}e^{-i\xi x}\,dx \\=&\frac{Ai}{2\sqrt{2\pi}\mu}\int_{-\infty}^{\infty}\bra{e^{-\mu x^2}}'e^{-i\xi x}\,dx\end{align*}$

となる．部分積分により

$\begin{align*}&\frac{Ai}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\bra{e^{-\mu x^2}}'e^{-i\xi x}\,dx \\=&\frac{Ai}{\sqrt{2\pi}}\bra{\brc{e^{-\mu x^2}e^{-i\xi x}}_{-\infty}^{\infty}-\int_{-\infty}^{\infty}e^{-\mu x^2}\bra{e^{-i\xi x}}'\,dx} \\=&-\frac{Ai}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\mu x^2}(-i\xi)e^{-i\xi x}\,dx \\=&-\frac{\xi}{\sqrt{2\pi}}\int_{-\infty}^{\infty}G(x)e^{-i\xi x}\,dx =-\xi\hat{G}(\xi)\end{align*}$

が成り立つ．よって，$\hat{G}$は１階線形常微分方程式

$\begin{align*}&\od{\hat{G}}{\xi}(\xi)=-\frac{1}{2\mu}\xi\hat{G}(\xi) \\\iff&\od{\hat{G}}{\xi}(\xi)+\sigma^2\xi\hat{G}(\xi)=0\end{align*}$

を満たす．

ステップ３（微分方程式を解く）

ステップ１とステップ２より，未知関数$u$, 変数$t$の微分方程式

$\begin{align*}\od{u}{t}(t)+\sigma^2tu(t)=0\end{align*}$

の解で$u(0)=A\sigma$を満たすものを求めればよい．

先ほど示した命題より$\sigma^2t$の不定積分のひとつとして$\dfrac{1}{2}\sigma^2t^2$がとれるから，両辺に$e^{\sigma^2t^2/2}$をかけることで

$\begin{align*}&e^{\sigma^2t^2/2}\od{u}{t}+e^{\sigma^2t^2/2}\sigma^2tu(t)=0 \\\iff&\od{}{t}\bra{e^{\sigma^2t^2/2}u(t)}=0 \iff e^{\sigma^2t^2/2}u(t)=C \\\iff&u(t)=Ce^{-\sigma^2t^2/2}\end{align*}$