ラグランジュの未定乗数法は,次の問題のように$x$, $y$が等式を満たして動くときの関数の極値の候補を求める方法です.
実数$x$, $y$が$y=x-3$を満たして動くとき,$f(x,y)=5x^2+5y^2+6xy-2$が極値をとる点$(x,y)$の候補を求めよ.
制約条件がない場合は,単純に2変数関数$f$の偏導関数を求めて
\begin{align*}\pd{f}{x}(x,y)=\pd{f}{y}(x,y)=0\end{align*}
を解けば,$f$が極値をとる点$(x,y)$の候補が得られますが,上の問題のように制約条件$y=x-3$があるとそう単純な方法では解けません.
この問題では制約条件$y=x-3$が簡単なので$y$を消去して1変数に帰着させても解けますが,もっと複雑な制約条件ならそうもいきませんね.
この記事では
- ラグランジュの未定乗数法の直感的な考え方
- ラグランジュの未定乗数法(2変数)の具体例と証明
- 3変数以上の場合のラグランジュの未定乗数法
- 参考文献
を順に解説します.
ラグランジュの未定乗数法の直感的な考え方
まずは制約条件がある場合に,単純に$\displaystyle\pd{f}{x}(x,y)=\displaystyle\pd{f}{y}(x,y)=0$を解くだけでは解けない理由を説明し,ラグランジュの未定乗数法の直感的な考え方を説明します.
偏導関数から分かること
関数$f$の$x$に関する偏導関数$\displaystyle\pd{f}{x}$は$y$を固定したときの$f$の$x$の増減を表すのでした.
つまり,$\displaystyle\pd{f}{x}$は$x$のみを動かしたときの($x$軸に平行な向きの)増減を教えてくれるものになっています.
しかし,軸に平行でない直線や曲線上での増減は単純に偏導関数を考えるだけでは分かりません.
これにより,制約条件のもとでは単に偏導関数を考えるだけでは都合が悪いわけですね.
極値をとる2つのパターン
具体的に冒頭の問題を考えましょう.
(再掲)実数$x$, $y$が$y=x-3$を満たして動くとき,$f(x,y)=5x^2+5y^2+6xy-2$で定まる2変数関数$f$が極値をとる点$(x,y)$の候補を求めよ.
$z=f(x,y)$とすると$x$と$y$を決めると$z$が決まり,この方程式のグラフは$xyz$空間上に描くことができます.
この問題では,$f(x,y)$は2次の係数が全て正の2次式なので,$z=f(x,y)$のグラフは下に凸な以下のような「お椀型」の曲面となりますね.
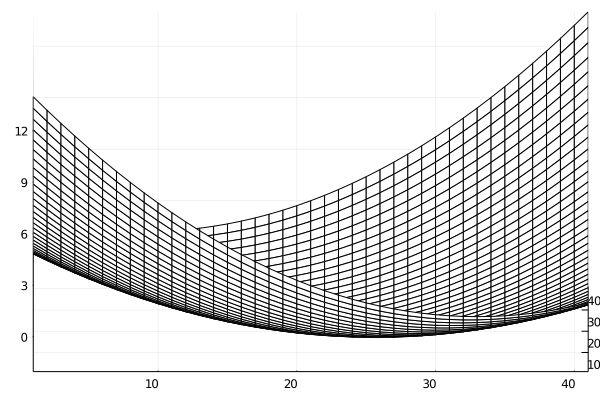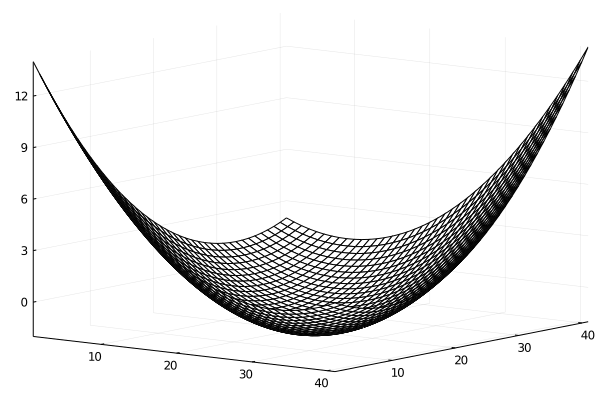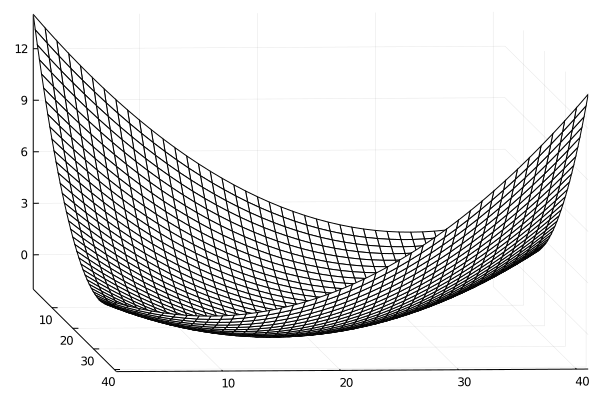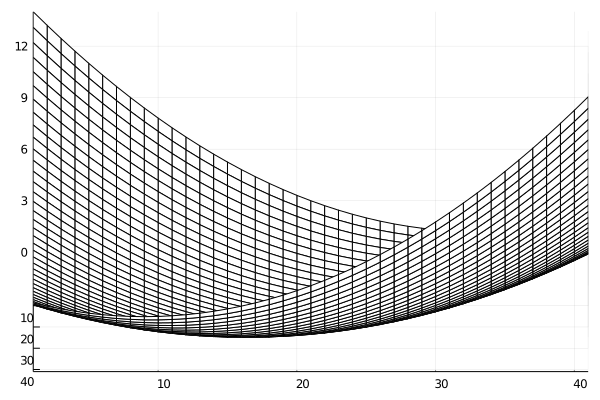
ラグランジュの未定乗数法の直観的な考え方で重要になるのは,$z=f(x,y)$のグラフを$z$軸に垂直な平面で切った「等高線」です.
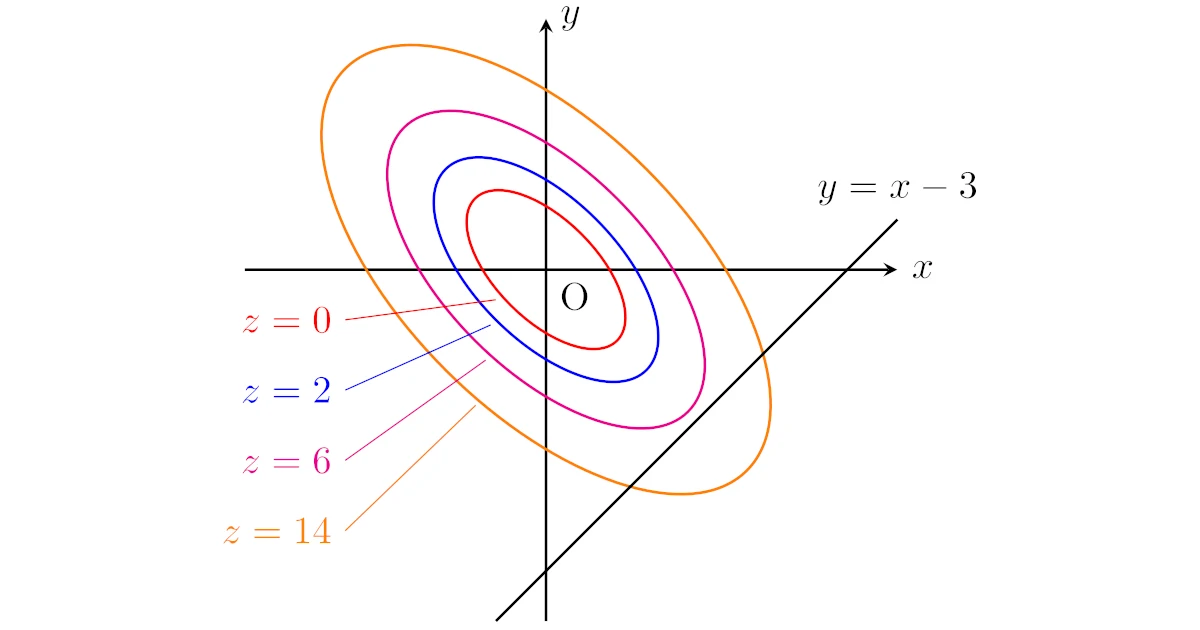
例えば,いまの$z=f(x,y)$のグラフの$z=0,2,6,14$での「等高線」は下図のようになります.
$z=0,2,6,14$と$z$が大きくなるにつれて等高線が広がっているのが見てとれますね.
パターン1(等高線と制約条件のグラフが接する)
こうみるとうまく$z=C$を取れば,等高線$f(x,y)=C$は制約条件$y=x-3$のグラフと接するようにできそうです.
もし等高線$f(x,y)=C$と$y=x-3$が点$(a,b)$で接するなら,下図のようになります.
さて,この等高線$f(x,y)=C$は$xy$平面を2つの領域に分割しており,
- 等高線$f(x,y)=C$の内部では$f(x,y)<C$
- 等高線$f(x,y)=C$の外部では$f(x,y)>C$
となっていますから,制約条件$y=x-3$上の点$(x,y)$は$f(x,y)\ge C$を満たし,$f(a,b)=C$だから,制約条件$y=x-3$のもとでの$f(x,y)$の最小値は$C$であることが分かりますね.
このように「制約条件$g(x,y)=0$のグラフ」と「$z=f(x,y)$の等高線」が接するような点$(a,b)$を見つけることができれば,この点$(a,b)$は極値となりえますね.
いま考えている問題では$g(x,y)=y-x+3$とすれば,制約条件は$g(x,y)=0$となりますね.
さて,制約条件$g(x)=0$のグラフと等高線$f(x,y)=C$が点$(a,b)$で接するなら
- $g(x,y)=0$上の点$(a,b)$での法線ベクトル$\nabla g(a,b)=\bmat{\pd{g}{x}(a,b)\\\pd{g}{y}(a,b)}$
- $f(x,y)=C$上の点$(a,b)$での法線ベクトル$\nabla f(a,b)=\bmat{\pd{f}{x}(a,b)\\\pd{f}{y}(a,b)}$
は平行となりますね.
このとき,($\nabla{g}\neq\m{0}$なら)ある$\mu\in\R$が存在して
\begin{align*}\nabla{f}=\mu\nabla{g}
\iff \bmat{\pd{f}{x}(a,b)\\\pd{f}{y}(a,b)}=\mu\bmat{\pd{g}{x}(a,b)\\\pd{g}{y}(a,b)}\end{align*}
が成り立ちます.よって,この等式が成り立つとき,点$(a,b)$は極値となり得ます.
パターン2(制約条件が尖っている)
今考えていた制約条件$y=x-3$は滑らかな曲線でしたが,制約条件によってはグラフが「尖る」ことがあります.
このような尖った点では接ベクトルを考えることができませんが,もしこのグラフの尖った点が等高線$f(x,y)=C$にタッチしてすぐに引き返す状況になっていれば極値をとりうるわけです.
のちにラグランジュの未定条数法の具体例を考えますが,そこでの例2がこのパターン2に相当します.
$g$が微分可能であるとすれば,制約条件$g(x,y)=0$のグラフが尖る可能性があるのは$g$の速度が0になるような場合です.つまり,$g(x,y)=0$上の点$(a,b)$が
\begin{align*}\pd{g}{x}(a,b)=\pd{g}{y}(a,b)=0\end{align*}
を満たしていれば,$g(x,y)=0$のグラフは点$(a,b)$で尖っている可能性がありますね.
つまり,このような$(a,b)$は極値の候補になるわけですね.
ラグランジュの未定乗数法(2変数)の具体例と証明
以上の考察をまとめると次のようになり,この定理をラグランジュ(Lagrange)の未定乗数法といいます.
[ラグランジュの未定乗数法(2変数の場合)]関数$f,g:\R^2\to\R$は共に$C^1$級であるとする.
制約条件$g(x,y)=0$における$f$が点$(a,b)$で極値をとるとき,次の(1), (2)のいずれかが成り立つ.
- $\displaystyle\pd{g}{x}(a,b)=\displaystyle\pd{g}{y}(a,b)=0$かつ$g(a,b)=0$が成り立つ.
- $\bmat{\pd{f}{x}(a,b)\\\pd{f}{y}(a,b)}=\mu\bmat{\pd{g}{x}(a,b)\\\pd{g}{y}(a,b)}$かつ$g(a,b)=0$を満たす$\mu\in\R$が存在する.
ラグランジュの未定乗数法は制約条件上の極値をもつときに成り立つ条件を述べているだけであり,(1)または(2)を満たしていても極値とならないこともあります.
具体例1(制約条件と等高線が接する場合)
実数$x$, $y$が$x^2+y^2=4$を満たして動くとき,$f(x,y)=(x-1)^2+(y-1)^2$が極値をとる点$(x,y)$の候補をラグランジュの未定乗数法により求めよ.
$g(x,y)=x^2+y^2-4$とおくと,制約条件は$g(x,y)=0$と表せる.$g(x,y)=0$のグラフ$S$は原点中心,半径2の円である.
(1) $\displaystyle\pd{g}{x}(x,y)=2x$, $\displaystyle\pd{g}{y}(x,y)=2y$なので
\begin{align*}\pd{g}{x}(x,y)=\pd{g}{y}(x,y)=0\iff x=y=0\end{align*}
であるが,$(0,0)\notin S$なので$\displaystyle\pd{g}{x}(a,b)=\displaystyle\pd{g}{y}(a,b)=0$となる$(a,b)\in S$は存在しない.
(2) $x$, $y$, $\lambda$連立方程式
\begin{align*}\begin{cases}\pd{f}{x}(x,y)=\lambda\pd{g}{x}(x,y)
\\\pd{f}{y}(x,y)=\lambda\pd{g}{y}(x,y)
\\g(x,y)=0\end{cases}
\iff\begin{cases}(1-\lambda)x=1
\\(1-\lambda)y=1
\\x^2+y^2=4\end{cases}\quad\dots(*)\end{align*}
の解$(x,y,\lambda)=(a,b,\mu)$が存在すれば点$(a,b)$が極値点の候補となる.
第3式の両辺を$(1-\lambda)^2$倍して,第1式と第2式を代入することにより
\begin{align*}&(1-\lambda)^2x^2+(1-\lambda)^2y^2=4(1-\lambda)^2
\\\iff&1^2+1^2=4(1-\lambda)^2
\\\iff&\lambda=1\mp\frac{1}{\sqrt{2}}\end{align*}
を得る.それぞれの$\lambda$を$(1-\lambda)x=1$と$(1-\lambda)y=1$に代入して,複号同順で
\begin{align*}(x,y)=\bra{\pm\sqrt{2},\pm\sqrt{2}}\end{align*}
となって連立方程式$(*)$の解が求まった(よって,存在した).
(1), (2)より,極値点の候補$\bra{\pm\sqrt{2},\pm\sqrt{2}}$が得られた.
具体例2(制約条件のグラフが尖る場合)
実数$x$, $y$が$x^2=y^3$を満たして動くとき,$f(x,y)=(x-1)^2+y^3$が極値をとる点$(x,y)$の候補をラグランジュの未定乗数法により求めよ.
$g(x,y)=x^2-y^3$とおくと,制約条件は$g(x,y)=0$と表せる.$g(x,y)=0$のグラフ$S$は下図のようになる.
(1) $\displaystyle\pd{g}{x}(x,y)=2x$, $\displaystyle\pd{g}{y}(x,y)=-3y$なので
\begin{align*}\pd{g}{x}(x,y)=\pd{g}{y}(x,y)=0\iff x=y=0\end{align*}
であり,$(0,0)\in S$なので$(0,0)$は極値点の候補である.
(2) $x$, $y$, $\lambda$連立方程式
\begin{align*}\begin{cases}\pd{f}{x}(x,y)=\lambda\pd{g}{x}(x,y)
\\\pd{f}{y}(x,y)=\lambda\pd{g}{y}(x,y)
\\g(x,y)=0\end{cases}
&\iff\begin{cases}2(x-1)=2\lambda x
\\3y^2=-3\lambda y^2
\\x^2=y^3\end{cases}
\\&\iff\begin{cases}(1-\lambda)x=1
\\(1+\lambda)y^2=1
\\x^2=y^3\end{cases}\quad\dots(*)\end{align*}
の解$(x,y,\lambda)=(a,b,\mu)$が存在すれば点$(a,b)$が極値点の候補となる.
第2式より$\lambda=-1$または$y=0$が成り立つ.もし$y=0$なら第3式から$x=0$となるが,これは第1式に矛盾するから$y\neq0$なので,$\lambda=-1$である.
$\lambda=-1$を第1式と第3式に代入して$x=\frac{1}{2}$, $y=\frac{1}{\sqrt[3]{4}}$となって連立方程式$(*)$の解が求まった(よって,存在した).
(1), (2)より,極値点の候補$(0,0)$, $\bra{\dfrac{1}{2},\dfrac{1}{\sqrt[3]{4}}}$が得られた.
ラグランジュの未定乗数法(2変数)の証明
のちに2変数とは限らない一般の場合の証明を与えますが,ここでは2変数の場合の場合の証明を与えておきます.
制約条件$g(x,y)=0$における$f$が点$(a,b)$で極値をとることから$g(a,b)=0$が成り立つ.条件(1)が成り立たないときに,条件(2)が成り立つこと示せばよい.
$\bra{\displaystyle\pd{g}{x}(a,b),\displaystyle\pd{g}{y}(a,b)}\neq(0,0)$のとき,$\displaystyle\pd{g}{x}(a,b)\neq0$または$\displaystyle\pd{g}{y}(a,b)\neq0$が成り立つが,どちらでも同様なので$\displaystyle\pd{g}{x}(a,b)\neq0$の場合を示せば十分である.
$\mu:=\frac{\pd{f}{x}(a,b)}{\pd{g}{x}(a,b)}$とおくと,$\displaystyle\pd{f}{x}(a,b)-\mu\displaystyle\pd{g}{x}(a,b)=0$が成り立つから,あとは
\begin{align*}\pd{f}{y}(a,b)=\pd{g}{y}(a,b)\end{align*}
を示せばよい.
$\displaystyle\pd{g}{x}(a,b)\neq0$より陰関数定理が適用できる.すなわち,$(a,b)$の近傍$W\times V\subset \R^2$ $(W\subset\R,V\subset\R)$と,$C^1$級関数$h:V\to W$が存在して
- $(x,y)\in W\times V$なら,$x=h(y)$
- $\displaystyle\pd{h}{y}(b)=-\frac{\pd{g}{y}(a,b)}{\pd{g}{x}(a,b)}$
をみたす.また,$F:V\to \R$を$F(y):=f(h(y))$で定めると,$(h(b),b)\in S$であり,$f$が$S$上の点$(a,b)\in S$で極値をとることより,$F$は$V$上の点$b$で極値をもつから$\displaystyle\pd{F}{y}(b)=0$を満たす.
よって,$\mu$の定義と併せると
\begin{align*}\pd{f}{y}(a,b)-\mu\pd{g}{y}(a,b)
&=\pd{f}{y}(a,b)-\frac{\pd{f}{x}(a,b)}{\pd{g}{x}(a,b)}\cdot\pd{g}{y}(a,b)
\\&=\pd{f}{y}(a,b)+\pd{f}{x}(a,b)\pd{h}{y}(b)
\\&=\pd{F}{y}(b)=0\end{align*}
だから$\displaystyle\pd{f}{y}(a,b)=\mu\displaystyle\pd{g}{y}(a,b)$が従う.
ラグランジュ関数$\Phi(x,y,\lambda)=f(x,y)-\lambda g(x,y)$
上の定理の書き方で何も問題ありませんが,ラグランジュの未定乗数法の(2)は
\begin{align*}\Phi(x,y,\lambda)=f(x,y)-\lambda g(x,y)\end{align*}
で定まる3変数関数$\Phi$を用いるともう少しスッキリ表すことができます.
$\Phi$を各変数$x$, $y$, $\lambda$で偏微分すると
\begin{align*}\begin{cases}\pd{\Phi}{x}=\pd{f}{x}-\lambda \pd{g}{x}
\\\pd{\Phi}{y}=\pd{f}{y}-\lambda \pd{g}{y}
\\\pd{\Phi}{\lambda}=-g(x,y)\end{cases}\end{align*}
となるので,(2)の条件は「$\displaystyle\pd{\Phi}{x}(a,b,\mu)=\displaystyle\pd{\Phi}{x}(a,b,\mu)=\displaystyle\pd{\Phi}{x}(a,b,\mu)=0$を満たす$a,b,\mu\in\R$が存在する」と書区こともできますね.
この関数$\Phi$はラグランジュ関数と呼ばれます.
3変数以上の場合のラグランジュの未定乗数法
2変数の場合のラグランジュの未定乗数法を$N$変数に拡張すると次のようになります.
[ラグランジュの未定乗数法]関数$f,g_1,\dots,g_k:\R^N\to\R$は全て$C^1$級であるとする.
制約条件$g(\m{x})=0$における$f$が点$\m{a}$で極値をとるとき,次の(1), (2)のいずれかが成り立つ.
- $\rank{\bmat{\pd{g_1}{x_1}(\m{a})&\dots&\pd{g_1}{x_N}(\m{a})\\\vdots&\ddots&\vdots\\\pd{g_k}{x_1}(\m{a})&\dots&\pd{g_k}{x_N}(\m{a})}}<k$
- $\Phi(\m{x},\m{\lambda})=f(\m{x})-\sum_{i=1}^{k}\lambda_{i}g_{i}(\m{x})$で定まる$\Phi:\R^N\times\R^k\to\R$に対して,$\nabla_{\m{x},\m{\lambda}}{\Phi}(\m{a},\m{\mu})=\m{0}$となる$\m{\mu}\in\R^k$が存在する.
ただし,$\m{\lambda}=\bmat{\lambda_1\\\vdots\\\lambda_k}$である.
$\m{g}=\bmat{g_1\\\vdots\\g_k}$とおく.任意の$i=1,\dots,N$に対して
\begin{align*}\pd{\m{g}}{x_i}(\m{x})
=\pd{}{x_i}\bmat{g_1(\m{x})\\\vdots\\g_k(\m{x})}
=\bmat{\pd{g_1}{x_i}(\m{x})\\\vdots\\\pd{g_k}{x_i}(\m{x})}\end{align*}
なので,条件(1)の条件は$\rank{\brc{\displaystyle\pd{\m{g}}{x_1}(\m{a}),\dots,\displaystyle\pd{\m{g}}{x_N}(\m{a})}}<k$と表せる.
証明の方針
制約条件$g(\m{x})=0$における$f$が点$\m{a}$で極値をとることから$g(\m{a})=0$が成り立つ.条件(1)が成り立たないときに,条件(2)が成り立つこと示せばよい.
$\rank{\brc{\displaystyle\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_N}(\m{a})}}=k$が成り立つとき$k\le N$であり,$\rank{\displaystyle\brc{\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_k}(\m{a})}}=k$としても一般性を失わない.
$\mu:=\frac{\pd{f}{x}(a,b)}{\pd{g}{x}(a,b)}$とおくと,$\displaystyle\pd{f}{x}(a,b)-\mu\displaystyle\pd{g}{x}(a,b)=0$が成り立つから,あとは
\begin{align*}\pd{f}{y}(a,b)=\pd{g}{y}(a,b)\end{align*}
を示せばよい.
$\m{\mu}\in\R^k$と$\Phi:\R^N\times\R^k\to\R$を
\begin{align*}
&\m{\mu}^T:=\brc{\pd{f}{x_1}(\m{a}),\dots,\pd{f}{x_k}(\m{a})}\brc{\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_k}(\m{a})}^{-1}\\
&\bra{\begin{aligned}
\iff&\m{\mu}^T\brc{\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_k}(\m{a})}=\brc{\pd{f}{x_1}(\m{a}),\dots,\pd{f}{x_k}(\m{a})}
\\\iff&\brc{\m{\mu}^{T}\pd{\m{g}}{x_1}(\m{a}),\dots,\m{\mu}^{T}\pd{\m{g}}{x_k}(\m{a})}=\brc{\pd{f}{x_1}(\m{a}),\dots,\pd{f}{x_k}(\m{a})}
\end{aligned}},
\\&\Phi(\m{x},\m{\lambda}):=f(\m{x})-\m{\lambda}\m{g}(\m{x})\end{align*}
で定めると,$\nabla_{\m{x},\m{\lambda}}{\Phi}(\m{a},\m{\mu})=\m{0}$が成り立つことを示せば良い.これを以下で示す.
$\displaystyle\pd{\Phi}{\lambda_i}(\m{a},\m{\mu})=0$($i=1,\dots,k$)の証明
$\m{a}\in S$より$g_i(\m{a})=0$ ($i=1,\dots,k$)なので
\begin{align*}\pd{\Phi}{\lambda_i}(\m{a},\m{\mu})=-g_i(\m{a})=0\end{align*}
が従う.
$\displaystyle\pd{\Phi}{x_i}(\m{a},\m{\mu})=0$($i=1,\dots,k$)の証明
$\Phi$と$\m{\mu}$の定義から,任意の$i=1,\dots,k$に対して
\begin{align*}\pd{\Phi}{x_i}(\m{a},\m{\mu})
=&\pd{f}{x_i}(\m{a})-\m{\mu}\cdot\pd{\m{g}}{x_i}(\m{a})
\\=&\pd{f}{x_i}(\m{a})-\m{\mu}^{T}\pd{\m{g}}{x_i}(\m{a})
\\=&\pd{f}{x_i}(\m{a})-\pd{f}{x_i}(\m{a})
=0\end{align*}
が従う.
$\displaystyle\pd{\Phi}{x_i}(\m{a},\m{\mu})=0$($i=k+1,\dots,N$)の証明
$\m{a}=(\m{a}_1,\m{a}_2)\in\R^k\times\R^{N-k}$とする.$\rank{\brc{\displaystyle\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_k}(\m{a})}}=k$より$\m{a}$の近傍で陰関数定理が適用できる.すなわち,
- $\m{a}$の近傍$W\times V\subset \R^N$ $(W\subset\R^k,V\subset\R^{N-k})$
- $C^1$級関数$\m{h}=\bmat{h_1\\\vdots\\h_k}:V\to W$
が存在して,任意の$\m{x}=(\m{x}_1,\m{x}_2)\in W\times V$は
\begin{align*}\m{x}\in S
\iff\m{g}(\m{x})=\m{0}
\iff \m{x}_1=\m{h}(\m{x}_2)\end{align*}
かつ
\begin{align*}&\brc{\pd{\m{h}}{x_{k+1}}(\m{a}_2),\dots,\pd{\m{h}}{x_N}(\m{a}_2)}
\\=&-\brc{\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_k}(\m{a})}^{-1}\brc{\pd{\m{g}}{x_{k+1}}(\m{a}),\dots,\pd{\m{g}}{x_N}(\m{a})}\end{align*}
をみたす.$\m{\mu}$の定義と併せると
\begin{align*}&\brc{\m{\mu}^{T}\pd{\m{g}}{x_{k+1}}(\m{a}),\dots,\m{\mu}^{T}\pd{\m{g}}{x_N}(\m{a})}
=\m{\mu}^{T}\brc{\pd{\m{g}}{x_{k+1}}(\m{a}),\dots,\pd{\m{g}}{x_N}(\m{a})}
\\=&\brc{\pd{f}{x_1}(\m{a}),\dots,\pd{f}{x_k}(\m{a})}\brc{\pd{\m{g}}{x_1}(\m{a}),\dots,\pd{\m{g}}{x_k}(\m{a})}^{-1}\brc{\pd{\m{g}}{x_{k+1}}(\m{a}),\dots,\pd{\m{g}}{x_N}(\m{a})}
\\=&-\brc{\pd{f}{x_1}(\m{a}),\dots,\pd{f}{x_k}(\m{a})}\brc{\pd{\m{h}}{x_{k+1}}(\m{a}_2),\dots,\pd{\m{h}}{x_N}(\m{a}_2)}\end{align*}
だから,任意の$i=k+1,\dots,N$に対して,
\begin{align*}\m{\mu}^{T}\pd{\m{g}}{x_{i}}(\m{a})
=&-\brc{\pd{f}{x_1}(\m{a}),\dots,\pd{f}{x_k}(\m{a})}\pd{\m{h}}{x_{i}}(\m{a}_2)
\\=&-\sum_{j=1}^{k}\pd{f}{x_j}(\m{a})\pd{h_i}{x_i}(\m{a}_2)\end{align*}
となる.
また,$F:V\to \R$を
\begin{align*}F(\m{x}_2):=f(h_1(\m{x}_2),\dots,h_k(\m{x}_2),\m{x}_2)\end{align*}
で定める.このとき,$(h_1(\m{x}_2),\dots,h_k(\m{x}_2),\m{x}_2) \in S$であり,$f$が$S$上の点$\m{a}$で極値をとるという仮定より,$F$は$V$上の点$\m{a}_2$で極値をもつから,$\displaystyle\pd{F}{x_{k+1}}(\m{a}_2)=\dots=\pd{F}{x_N}(\m{a}_2)=0$を満たす.
よって,任意の$i=k+1,\dots,N$に対して,
\begin{align*}\pd{\Phi}{x_i}(\m{a},\m{\mu})
=&\pd{f}{x_i}(\m{a})-\m{\mu}\cdot\pd{\m{g}}{x_{i}}(\m{a})
=\pd{f}{x_i}(\m{a})-\m{\mu}^{T}\pd{\m{g}}{x_{i}}(\m{a})
\\=&\pd{f}{x_i}(\m{a})+\sum_{j=1}^{k}\pd{f}{x_j}(\m{a})\pd{h_i}{x_i}(\m{a}_2)
=\pd{F}{x_i}(\m{a}_2)=0\end{align*}
が従う.
参考文献
以下は参考文献です.
解析入門
[杉浦光男 著/東京大学出版会]
解析学の教科書としては非常に有名で,理論系で解析がしっかり必要となる人は持っておいてよいテキストです.
- 第1巻で1変数の微分積分学
- 第2巻で多変数の微分積分学
を扱っています.本書に対応した演習書「解析演習」も出版されています.
本書の特徴としては
- 数学的に厳密に書かれている
- 基本的な微分積分学の知識体系は網羅されている
の2点が挙げられます.
このため,辞書的に使う教科書という位置付けて持っている人も多いようです.
なお,この記事の内容は第1巻に載っています.
微分積分学
[笠原晧司 著/サイエンス社]
微分積分学の教科書として有名な名著です.
具体例を多く扱いイメージを掴むことに重点を置きつつ,議論もきっちりしているため,大学1年生の微分積分学をしっかり学びたい人には心強い味方になると思います.
具体例のレベルは基本的なものに加えて少々難しいものも含まれているので,いろいろな具体例に触れたい人は持っておいてもよいでしょう.
このため,しっかり数学をやりたい人の微分積分学の導入としてオススメできる一冊です.



コメント
とても明快なご説明ありがとうございました。イメージがつかめず困っていたため、大変助かりました。
コメントをありがとうございます!
公式を見ても,なかなかイメージか掴みづらいものもありますよね.
お役に立てたようで良かったです!