 ルベーグ積分の基本
ルベーグ積分の基本 ルベーグ積分の定義|単関数による近似を踏まえて定義する
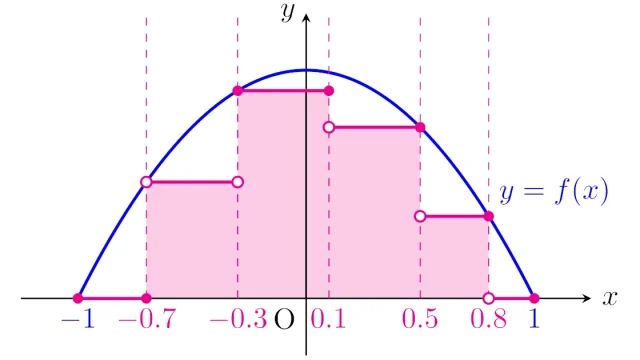
可測単関数にルベーグ積分は簡単に定義でき,非負可測関数fは非負可測単関数列{fₙ}でしたから近似できることを踏まえて,この記事では一般の可測関数にルベーグ積分を定義します.
 ルベーグ積分の基本
ルベーグ積分の基本 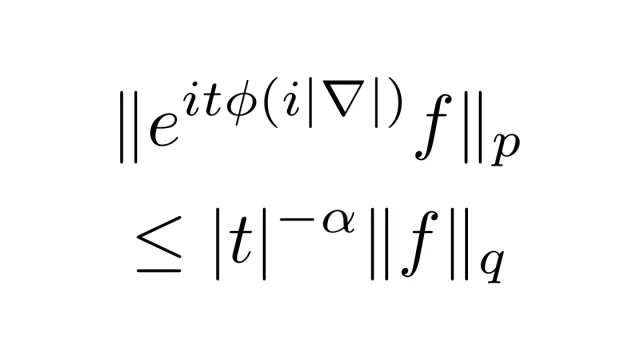 微分方程式
微分方程式 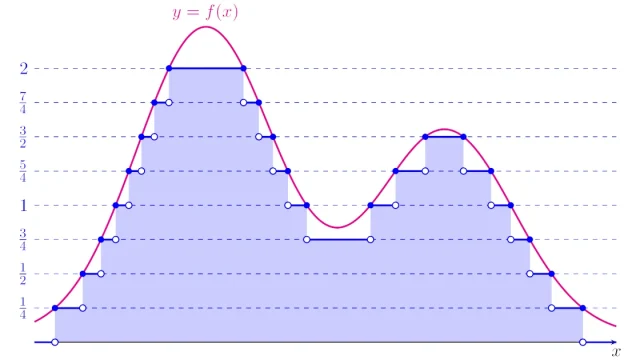 ルベーグ積分の基本
ルベーグ積分の基本 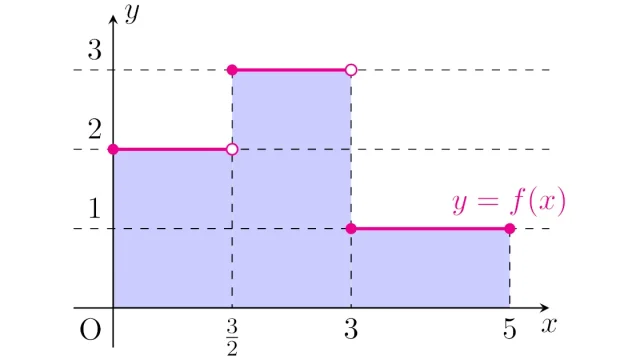 ルベーグ積分の基本
ルベーグ積分の基本 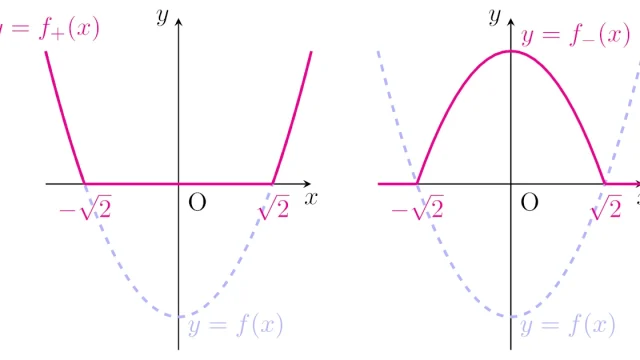 ルベーグ積分の基本
ルベーグ積分の基本 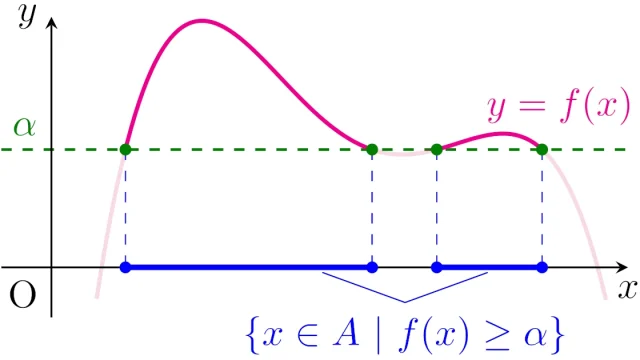 ルベーグ積分の基本
ルベーグ積分の基本  微分方程式
微分方程式 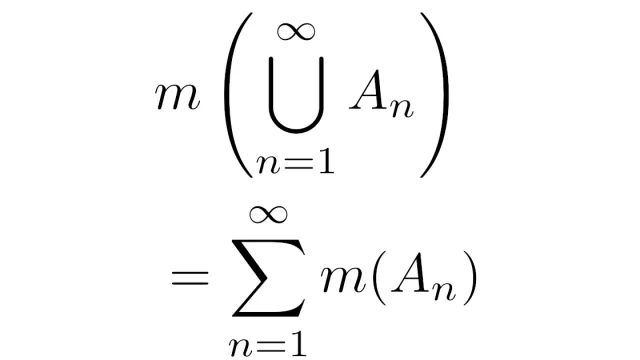 ルベーグ積分の基本
ルベーグ積分の基本 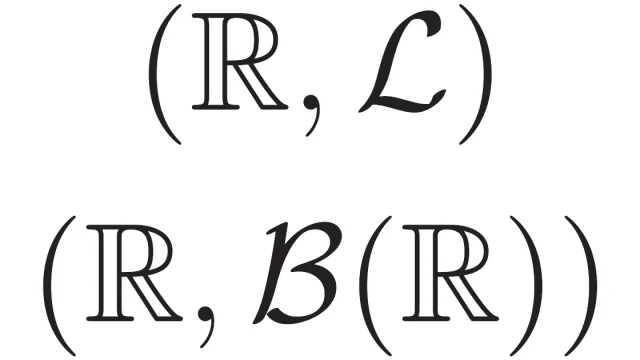 ルベーグ積分の基本
ルベーグ積分の基本  関数空間
関数空間