 微分積分学の基本
微分積分学の基本 関数の極限(収束)をε-δ論法で定義する|基本性質と発散も解説
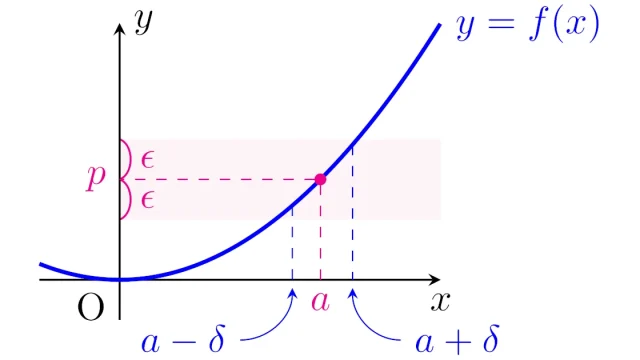
微分積分学では関数の極限x→aをε-δ論法で定義します.直観的には,ε-δ論法は「近い値を近い値に移す」という発想をもとにした論法になっています.また,同様の考え方でx→a±0の極限とx→±∞の極限も定義されます.
 微分積分学の基本
微分積分学の基本 正項級数の3つの基本の収束判定法|具体例とともに解説
級数の中でも正項級数の収束・発散の判定条件は多く知られており,とくに「比較定理(比較原理)」「ダランベールの判定法(ratio test)」「コーシーの判定法」は基本的です.この記事では,それぞれの判定法を具体例とともに解説します.
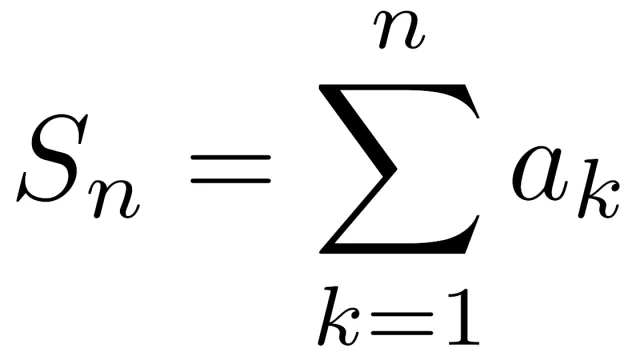 微分積分学の基本
微分積分学の基本 級数の考え方と厳密な定義|コーシーの条件・絶対収束も解説
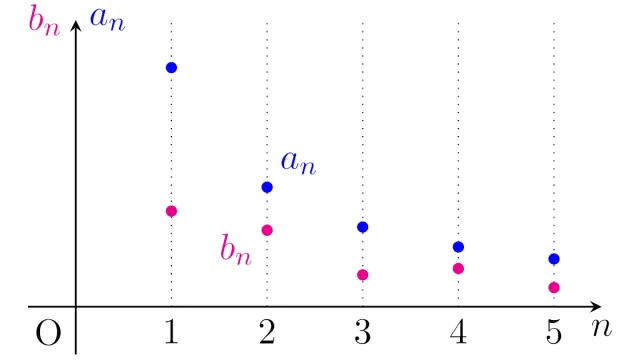
数列{aₙ}を初項から順に足し続けて値Sに近付くとき,{aₙ}の級数はSに収束するといいます.この記事では,級数の基本の考え方と定義から始めて,級数が収束するための必要十分条件であるコーシーの条件,十分条件である絶対収束を解説します.
 微分積分学の基本
微分積分学の基本 実数列{aₙ}はコーシー列なら収束する|便利さも併せて解説
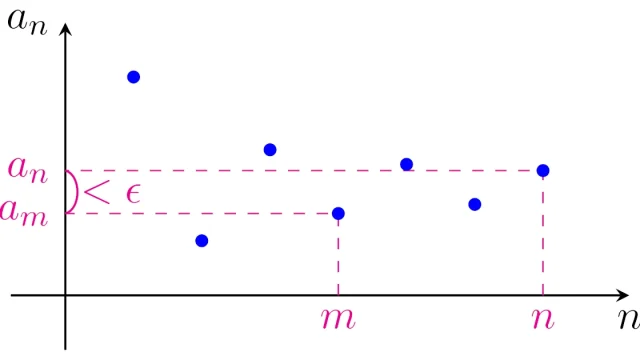
数列{aₙ}について,m,nを十分大きくすればaₙとa_mの誤差をどこまでも小さくできるとき,{aₙ}をコーシー列といいます.実数列ならコーシー列⇔収束列であり,このことから収束を簡単に示せる実数列があります.
 微分積分学の基本
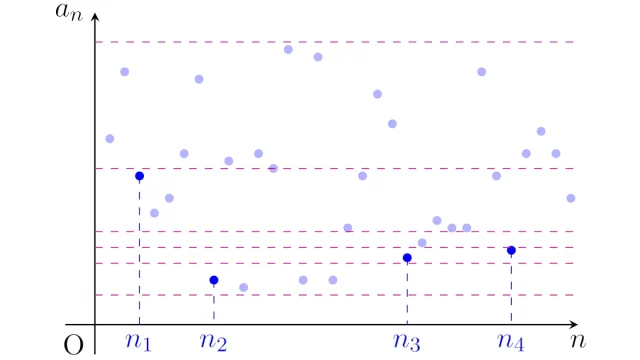
微分積分学の基本 ボルツァーノ-ワイエルシュトラスの定理|区間縮小法による証明
「有界実数列は収束する部分列をもつ」というボルツァーノ-ワイエルシュトラスの定理は「縁の下の力持ち」という言葉がよく似合う定理です.この記事では区間縮小法により,この定理を証明します.
 微分積分学の基本
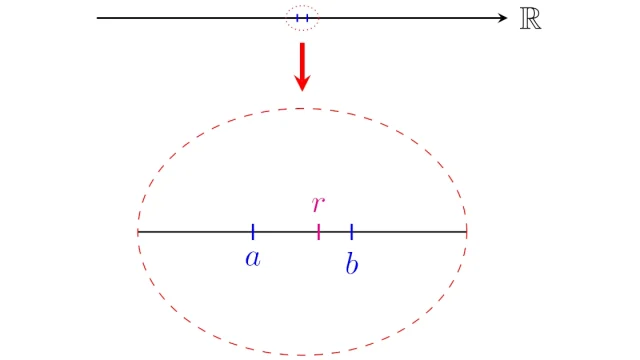
微分積分学の基本 有理数の稠密性|実数の「アルキメデスの性質」から証明する
有理数が実数(数直線)上に密に存在しているという性質を「有理数の集合の稠密性」といいます.この証明には「アルキメデスの性質」と呼ばれる実数の重要性質を用います.
 微分積分学の基本
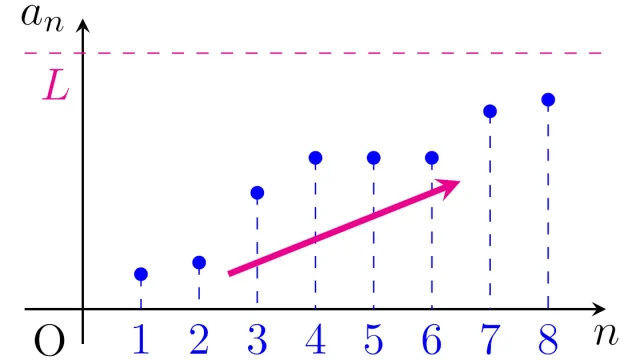
微分積分学の基本 単調有界実数列の収束定理|漸化式を解かずに極限を求める方法
一般に漸化式は解けるとは限らないので,漸化式を解かずに実数列{aₙ}の極限を求める方法があれば嬉しいですね.この記事では,単調収束定理を用いた実数列{aₙ}の極限の求め方を解説します.
 微分積分学の基本
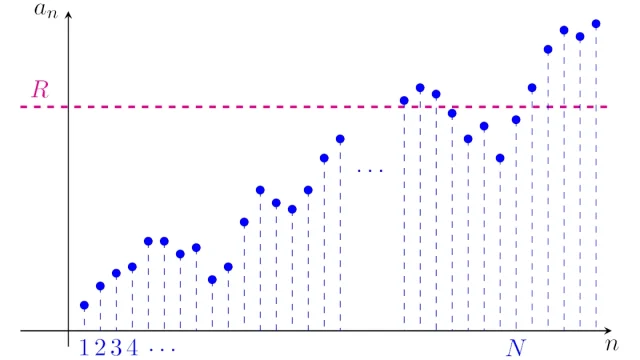
微分積分学の基本 収束しない実数列|実数列の3種類の発散と証明の例題
実数列{aₙ}が収束しないとき{aₙ}は発散するといいますが,発散には「∞に発散」「-∞に発散」「振動」の3種類があります.この記事では,これらの定義を厳密に扱い,具体例から証明の考え方も説明します.
 微分積分学の基本
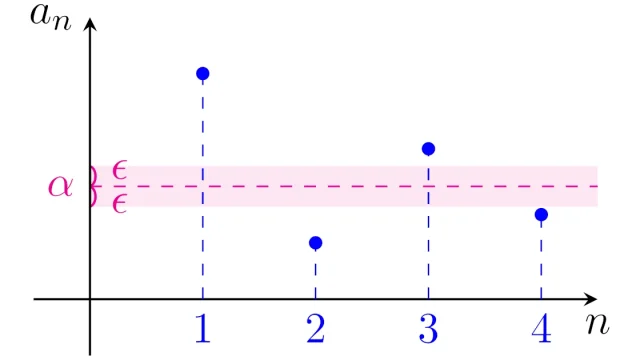
微分積分学の基本 数列の収束の定義(ε-N論法)|例題から考え方を理解しよう
高校数学では学ぶ数列の極限の定義は直感的で分かりやすいのですが,数学的には少々曖昧です.そこで,数列の極限を厳密に定義する方法として,この記事ではε-N論法をイメージから説明します.
 微分積分学の基本
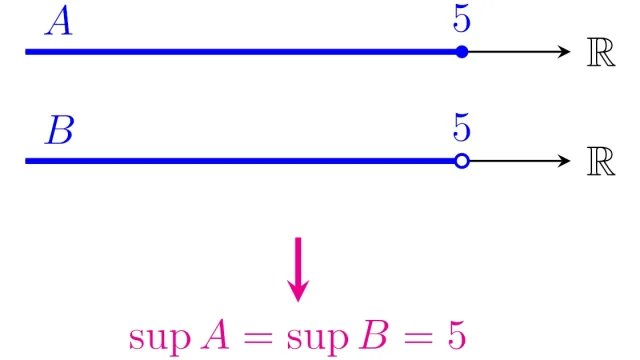
微分積分学の基本 上限supと下限inf|最大値max・最小値minより便利なヤツら
例えば,「5未満の実数全部の集合」には最大値は存在しませんが,「上限」は存在して5となります.この記事では,上限・下限の定義と基本性質を説明しています.
