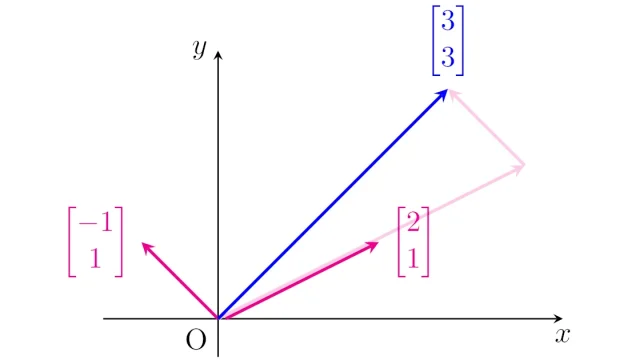
 線形空間の基本
線形空間の基本 線形結合・線形独立性の定義と例題|ベクトルたちの線形関係
ベクトルv₁,v₂,……,vₙたちのスカラー倍と和で表されるベクトルを線形結合と言います.また,v₁,v₂,……,vₙの線形結合で零ベクトルを作るために係数を全て0にするしかないとき,v₁,v₂,……,vₙは線形独立であると言います.
 線形空間の基本
線形空間の基本 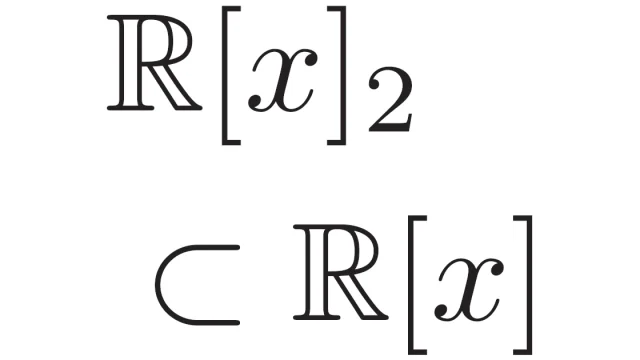 線形空間の基本
線形空間の基本 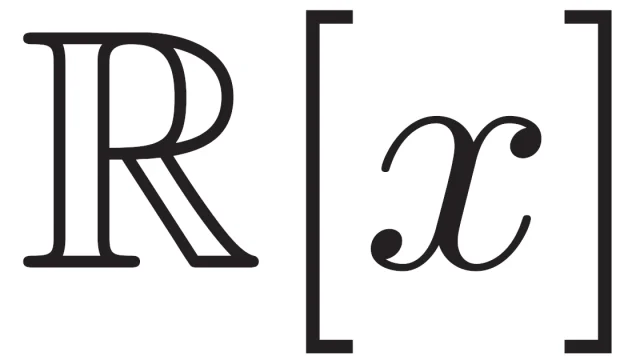 線形空間の基本
線形空間の基本 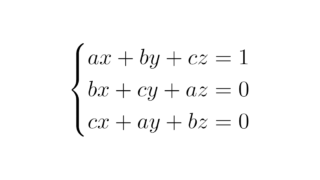 線形代数学
線形代数学 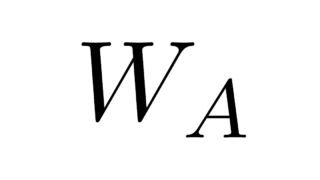 線形代数学の基本
線形代数学の基本 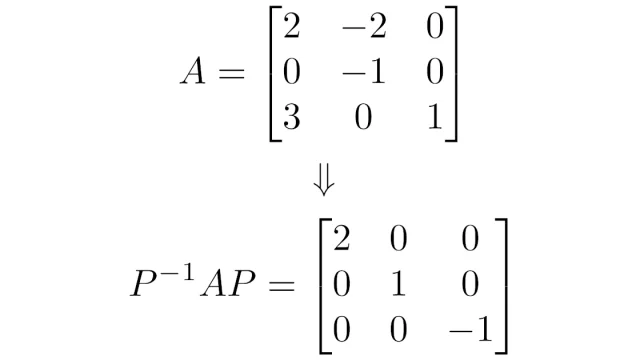 線形代数学の基本
線形代数学の基本 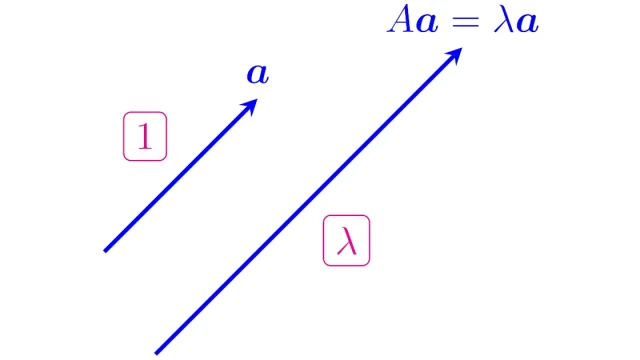 線形代数学の基本
線形代数学の基本 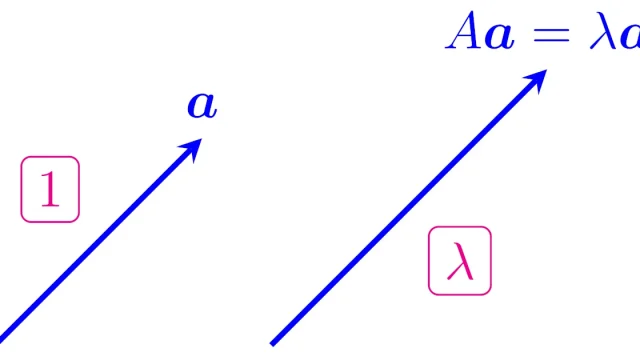 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本 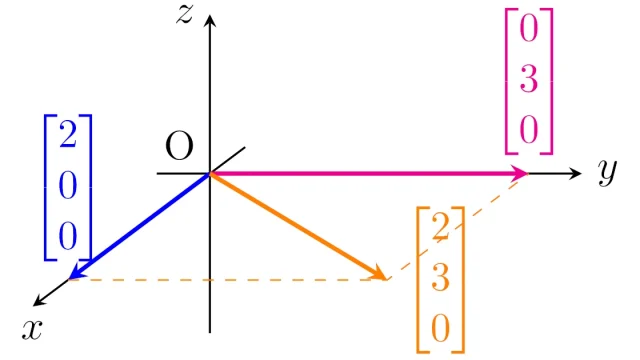 線形代数学の基本
線形代数学の基本