正方行列$A$の対角化は,$A$の固有値・固有ベクトルに密接に関わっているのでした.
そのため,正方行列を対角化するためには,固有値・固有ベクトルが求められるようになっておくことは大切です.
この記事では
- 固有方程式と固有値の求め方
- 固有ベクトルの求め方
を説明します.
なお,この記事の行列・ベクトルは特に断らない限り複素成分とします.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
固有方程式と固有値の求め方
正方行列の固有値は固有方程式を解くことによって求めることができます.
固有方程式の定義
固有値を求めるために,まずは固有方程式を準備します.
$n$次正方行列$A$に対して,
- $x$の多項式$|xI-A|$を$A$の固有多項式(characteristic polynomial)
- $x$の方程式$|xI-A|$を$A$の固有方程式(characteristic equation)
という.ただし,$I$は$n$次正方行列であり,$|xI-A|$は正方行列$xI-A$の行列式である.
最初は$|xI-A|$が$x$の多項式には見えないかもしれませんが,具体例を考えると$n$次多項式であることが見えてきます.
具体例1(2次正方行列)
正方行列$A=\bmat{1&2\\2&1}$の固有多項式と固有方程式を求めよ.また,固有方程式を解け.
$A=\bmat{1&2\\2&1}$の固有多項式は
\begin{align*}|xI-A|
=&\abs{x\bmat{1&0\\0&1}-\bmat{1&2\\2&1}}
=\vmat{x-1&-2\\-2&x-1}
\\=&(x-1)\cdot(x-1)-(-2)\cdot(-2)
\\=&x^2-2x-3
=(x-3)(x+1)\end{align*}
である.よって,固有方程式は$(x-3)(x+1)=0$であり,これを解くと$x=-1,3$である.
実際に行列式$|xI-A|$を計算することで$x$の2次式となっていることが見てとれますね.
具体例2(3次正方行列)
正方行列$B=\bmat{1&1&0\\2&0&0\\0&0&-1}$の固有多項式と固有方程式を求めよ.また,固有方程式を解け.
$B=\bmat{1&1&0\\2&0&0\\0&0&-1}$の固有多項式は
\begin{align*}|xI-B|
=&\abs{x\bmat{1&0&0\\0&1&0\\0&0&1}-\bmat{1&1&0\\2&0&0\\0&0&-1}}
=\vmat{x-1&-1&0\\-2&x&0\\0&0&x+1}
\\=&(x+1)\vmat{x-1&-1\\-2&x}
=(x+1)\{(x-1)\cdot x-(-1)\cdot(-2)\}
\\=&(x+1)(x^2-x-2)
=(x+1)^2(x-2)\end{align*}
である.よって,固有方程式は$(x+1)^2(x-2)=0$であり,これを解くと$x=-1,2$となる.
この例でも実際に行列式$|xI-A|$を計算することで,$x$の3次式となっていることが見てとれますね.
固有値の求め方
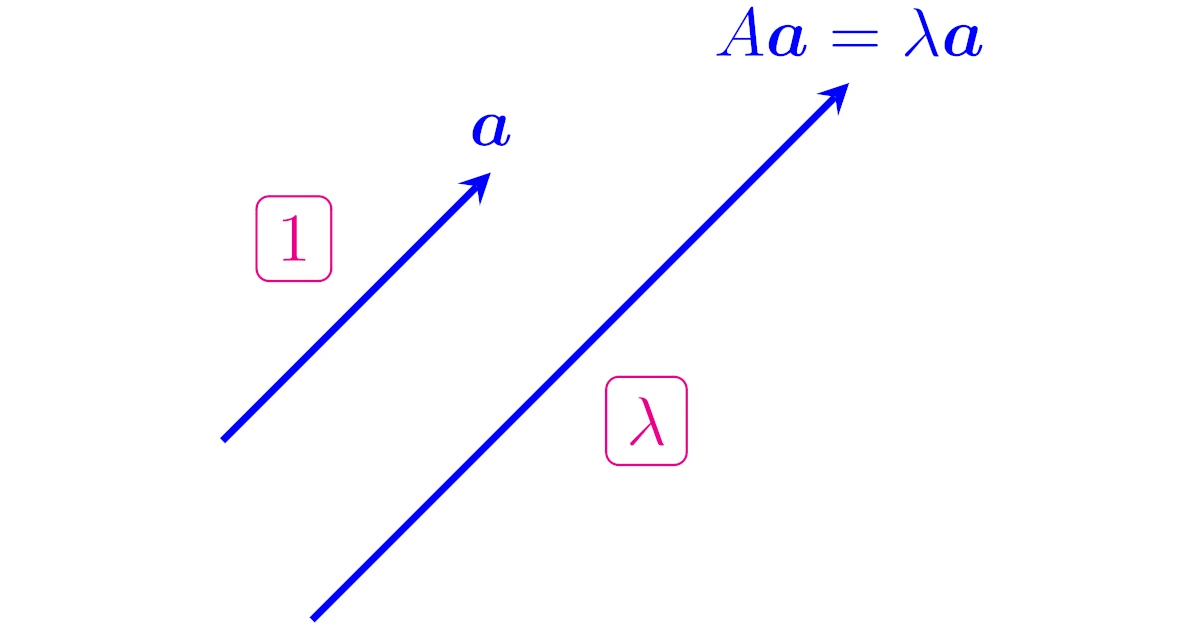
実は正方行列$A$に対して,$A$の固有値と$A$の固有方程式の解は一致します.すなわち,次が成り立ちます.
スカラー$\lambda$と正方行列$A$に対して,次は同値である.
- $\lambda$は$A$の固有値である.
- $\lambda$は$A$の固有方程式の解である.
この定理を用いると,上でみた具体例より
- $A=\bmat{1&2\\2&1}$の固有値は,固有方程式の解と一致して$-1$, $3$
- $A=\bmat{1&2&0\\2&0&0\\0&0&-1}$の固有値は,固有方程式の解と一致して$-1$, $2$
と分かりますね.
[$(1)\Ra(2)$の証明]$A$の固有値$\lambda$に属する固有ベクトルを$\m{p}$とする.
このとき,$A\m{p}=\lambda\m{p}$が成り立つから,移項して
\begin{align*}\m{0}=(\lambda I-A)\m{p}\end{align*}
が成り立つ.もし$\lambda I-A$が正則行列なら,両辺に左から$(\lambda I-A)^{-1}$をかけて$\m{0}=\m{p}$となるが,固有ベクトルの定義から$\m{p}\neq\m{0}$なので矛盾する.
よって,$\lambda I-A$は正則行列でないから,$|\lambda I-A|=0$を満たす.
[$(2)\Ra(1)$の証明]$|\lambda I-A|=0$が成り立つなら,$\m{x}$の連立1次方程式$(\lambda I-A)\m{x}=\m{0}$は$\m{0}$でない解$\m{p}$をもつ.
このとき,
\begin{align*}\m{0}=(\lambda I-A)\m{p}\iff A\m{p}=\lambda\m{p}\end{align*}
が成り立つから,$\lambda$は$A$の固有値(で,$\m{p}$は$A$の固有値$\lambda$に属する固有ベクトル)である.
$n$次正方行列$A$が複素行列なら,$A$の固有方程式$|xI-A|=0$は複素係数の$n$次方程式となります.
そのため,代数学の基本定理より$A$の固有方程式$|xI-A|=0$は重複を許して$n$個の複素数解をもつので,$A$は複素数の範囲に重複を許して$n$個の固有値を持ちます.
よって,複素正方行列の固有値は複素数の範囲で考えるのが普通です.
実数は複素数の一種なので,実正方行列も複素数の範囲に重複を許して$n$個の固有値を持ちます.
固有ベクトルの求め方
正方行列の固有値を求めることができれば,固有ベクトルを求めることができます.
$\lambda$が正方行列$A$の固有値と分かっていれば,$\m{0}$でない$\m{p}$に対して,固有値$\lambda$に属する固有ベクトルであることと
\begin{align*}A\m{p}=\lambda\m{p}\iff (A-\lambda I)\m{p}=\m{0}\end{align*}
であることは同値です.
さらにこれは$\m{p}$が$\m{x}$の連立1次方程式$(A-\lambda I)\m{x}=\m{0}$の解であることと同値ですから,この連立1次方程式を解けば固有ベクトルが得られますね.
正方行列$A=\bmat{1&2\\2&1}$の固有値を全て求め,それぞれの固有値に属する固有ベクトルも全て求めよ.
$\m{x}$の連立1次方程式$P\m{x}=\m{c}$は,拡大係数行列$[P,\m{c}]$に行基本変形を施すことで解けること(掃き出し法)を思い出しておきましょう.
$A=\bmat{1&2\\2&1}$の固有値が$-1$ ,$3$であることは上で説明したので
- 固有値$-1$に属する固有ベクトル
- 固有値$3$に属する固有ベクトル
を求めれば良い.
(1) $\m{p}_1$が$A$の固有値$-1$の固有ベクトルであることと,$\m{p}_1\neq\m{0}$かつ
\begin{align*}A\m{p}_1=(-1)\m{p}_1\iff(A+I)\m{p}_1=\m{0}\end{align*}
を満たすことは同値である.$A+I$は行基本変形により
\begin{align*}A+I
=\bmat{1&2\\2&1}+\bmat{1&0\\0&1}
=\bmat{2&2\\2&2}
\to\bmat{1&1\\0&0}\end{align*}
となるから,掃き出し法の考え方から$(A+I)\m{p}_1=\m{0}$の解は$\m{p}_1=c\bmat{1\\-1}$である.
よって,$A$の固有値$-1$に属する固有ベクトルは$c\bmat{1\\-1}$($c\neq0$)である.
(2) $\m{p}_2$が$A$の固有値$3$の固有ベクトルであることと
\begin{align*}A\m{p}_2=3\m{p}_2\iff(A-3I)\m{p}_2=\m{0}\end{align*}
を満たすことは同値である.$A-3I$は行基本変形により
\begin{align*}A-3I
=\bmat{1&2\\2&1}-3\bmat{1&0\\0&1}
=\bmat{-2&2\\-2&2}
\to\bmat{1&-1\\0&0}\end{align*}
となるから,掃き出し法の考え方から$(A-3I)\m{p}_2=\m{0}$の解は$\m{p}_2=d\bmat{1\\1}$である.
よって,$A$の固有値$3$に属する固有ベクトルは$d\bmat{1\\1}$($d\neq0$)である.
なお,$c\neq0$, $d\neq0$としているのは,固有ベクトルは$\m{0}$でないためです.
このように,固有ベクトルは各固有値に対して異なるものになるので,各固有値に対して求める必要があります.



コメント